前言
描述数据的统计学学意义是大数据分析的挖掘的基础,它包括数据的收集、整理、显示,对数据中的有用信息的
提取和分析,有利于我们更好地利用数据探索数据背后蕴藏的关系,下面是一些用来分析的统计量:
- 集中趋势的特征值: 算术平均数、调和平均数、几何平均数、众数、中位数等,其中均数适用于满足正态分布和对称分布的数据,中位数适用于所有的分布类型。
- 离散趋势的特征值:全距、内距、平均差、方差、标准差、标准误、离散系数。其中标准差、方差适用于正态分布的数据,标准误差实际上反映了数据偏离正态分布的程度。
工具:spss statistics22
数据来源:第15届华为杯研究生数学建模大赛C题
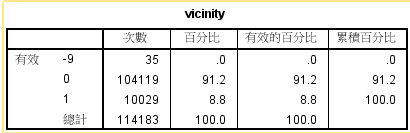
1、 频数分析,多用于离散数据,了解变量的取值状况,把握数据的分布特征。
- 频数:变量值落在某个区间中的次数。
- 百分比:各频数占总样本数的百分比。
- 有效百分比:各频数占有效本数的百分比。
- 累计百分比:各百分比逐级累加起来的结果。
2、绘制统计图,直接客观的刻画数据,展示变量的取值情况。
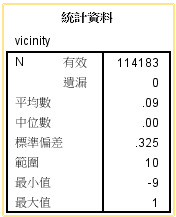
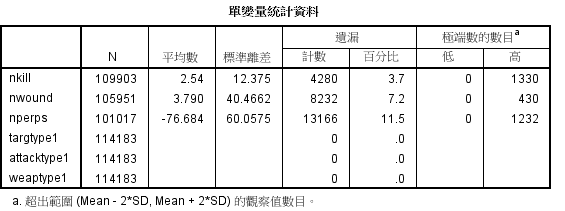
绘制4个缺失值较多的变量,进行散点绘图分析:
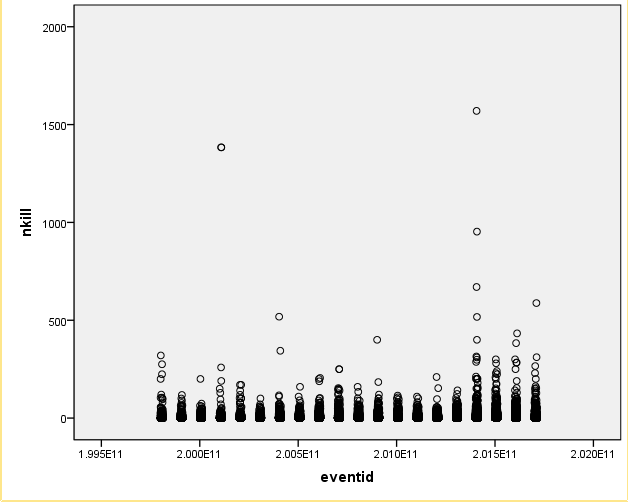
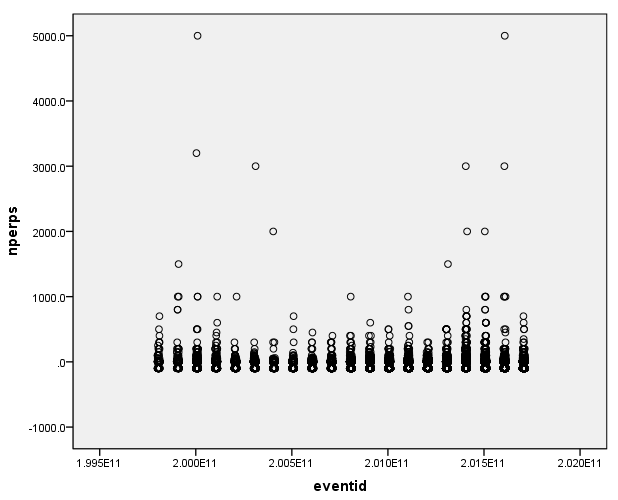
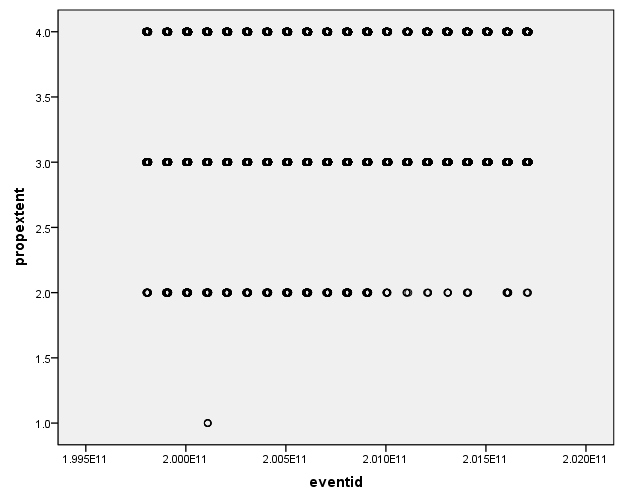
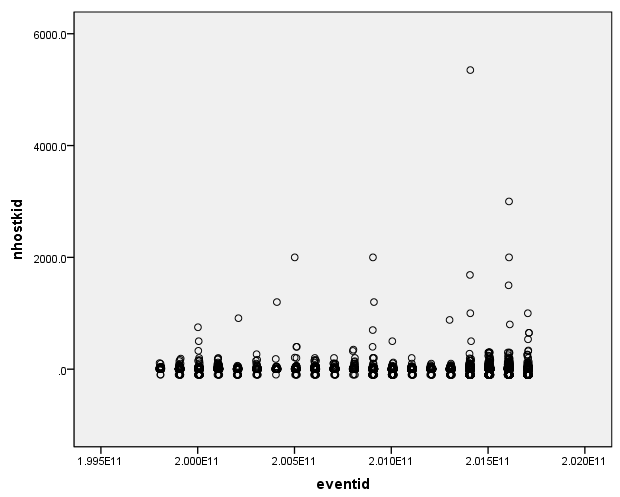
- 增加了误差差异,并降低了统计测试的能力
- 如果异常值是非随机分布的,则可以降低正态性
- 可能影响具有实质意义的估计
- 可能影响回归、方差分析等统计模型假设的基本假设。
因此在填补缺失值之前需要剔除异常值,。
使用回归分析的方法的前提是数据对象得先满足回归分析的基本假设如下:
1、随机误差项是一个期望值或平均值为0的随机变量;
2、对于解释变量的所有观测值,随机误差项有相同的方差;
3、随机误差项彼此不相关;
4、解释变量是确定性变量,不是随机变量,与随机误差项彼此之间相互独立;
5、解释变量之间不存在精确的(完全的)线性关系,即解释变量的样本观测值矩阵是满秩矩阵;
6、随机误差项服从正态分布。
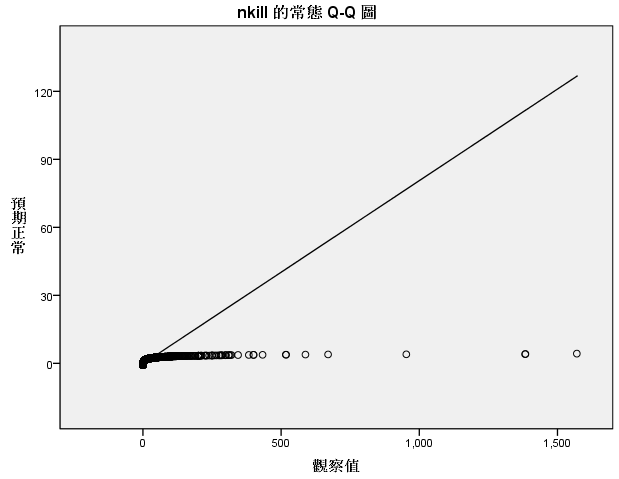
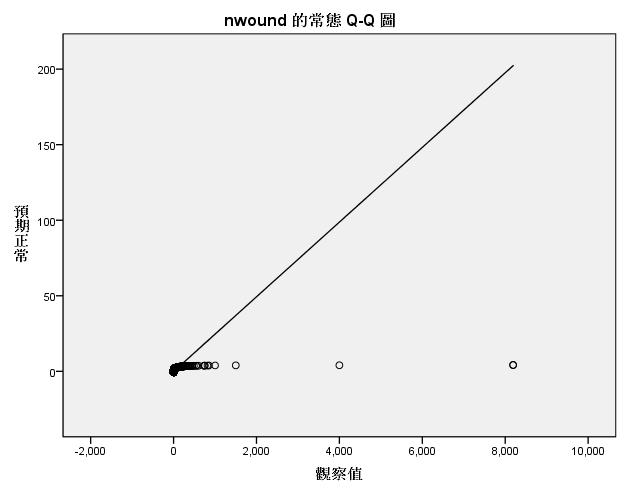
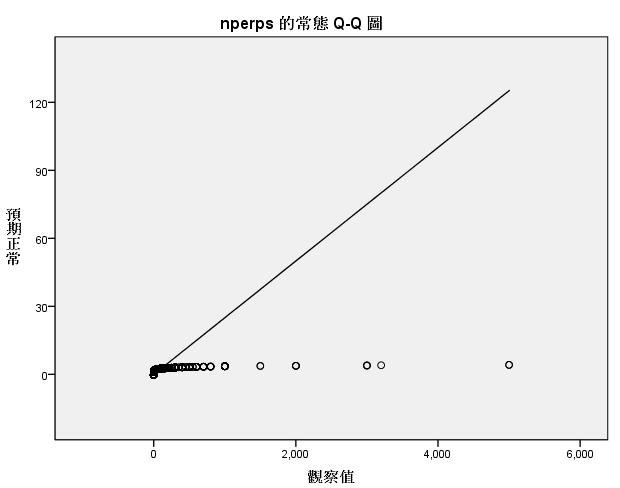
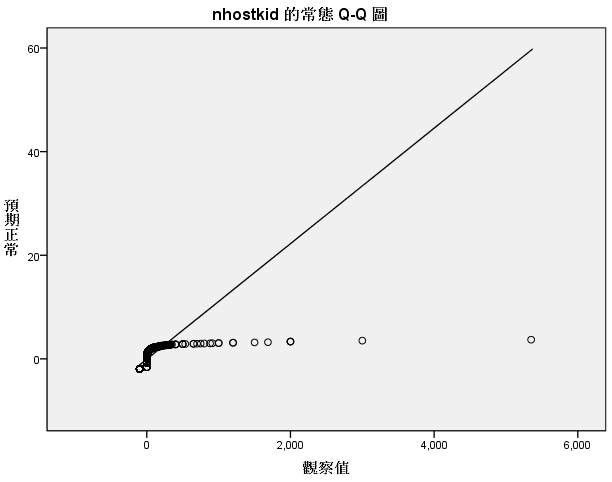
因此,这4个变量的填补都不能使用回归分析的方法进行填补。
利用最大期望法来进行缺失值的填补:
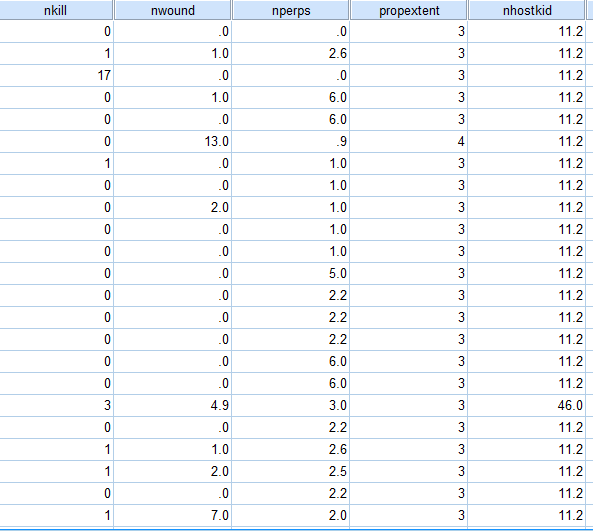




 本文探讨了大数据分析中统计量的应用,包括集中趋势和离散趋势的特征值,如算术平均数、中位数、标准差等,并讨论了频数分析、统计图绘制及异常值对数据分析的影响。通过案例分析,介绍了异常值处理和缺失值填补的方法,强调了在数据预处理阶段的重要性。
本文探讨了大数据分析中统计量的应用,包括集中趋势和离散趋势的特征值,如算术平均数、中位数、标准差等,并讨论了频数分析、统计图绘制及异常值对数据分析的影响。通过案例分析,介绍了异常值处理和缺失值填补的方法,强调了在数据预处理阶段的重要性。
















 3294
3294

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








