[数学][组合数] Jzoj P4257 着色

最新推荐文章于 2025-08-08 22:01:10 发布

转载最新推荐文章于 2025-08-08 22:01:10 发布 · 140 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Comfortable/p/10359003.html

文章标签：

#数据结构与算法

一个电子工程系学生使用K种颜料为涂色书上色，每幅图最多使用3种不同颜料且相邻区域颜色不同。文章探讨了如何计算合法的涂色方案数量，涉及算法设计和组合数学原理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

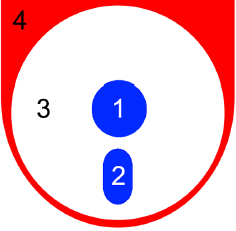
有个电子工程系的学生从小喜欢涂颜色。现在他买了本涂色书和K种不同的颜料开始涂色。有趣的是它并不喜欢色彩斑斓的图案，所以一幅图他最多只会用3种不同的颜料。还有，他不会把两个相邻区域涂成同样的颜色。当两个区域的边界至少有一个共同点时两个区域是相邻的。如下图，区域3和4是相邻的，区域1和2不是相邻的。下面的图给出了一种合法的涂色方案。

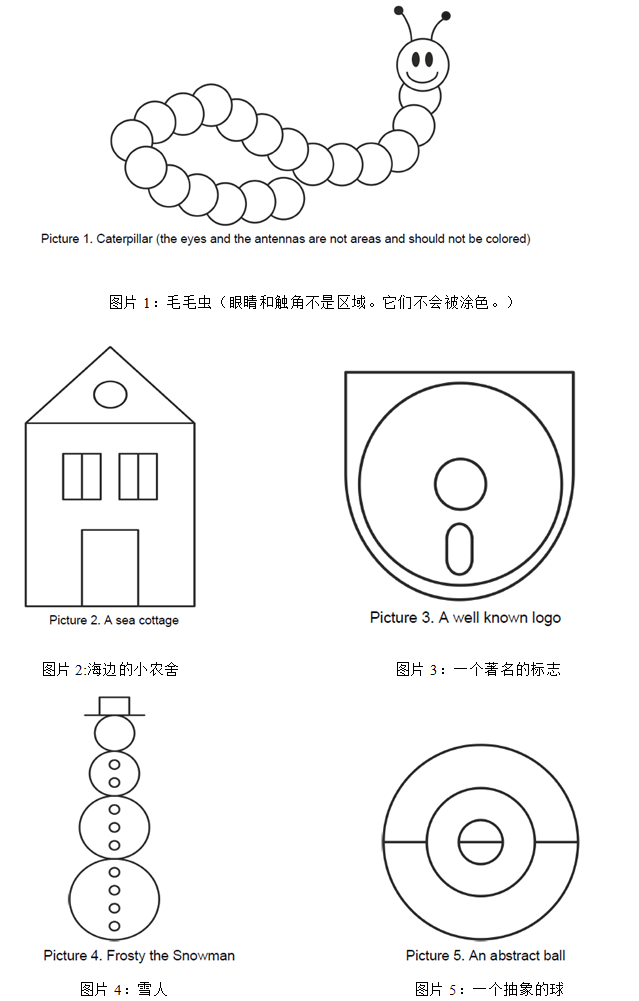
他想知道对于给定的一个图和颜料，有多少种合法的涂色方案。

Input

两个整数N（1<=N<=8），K（1<=K<=1000），N代表他要涂的是书里的第N张图片，K代表有K中不同的颜料选择。
这本书的内容请看后面！！

Output

输出一个整数。代表合法的方案数。

Sample Input

输入1：
2 2
输入2：
5 3
输入3：
7 3

Sample Output

输出1：
0
输出2：
12
输出3：
96

Data Constraint

N（1<=N<=8），K（1<=K<=1000）

Hint

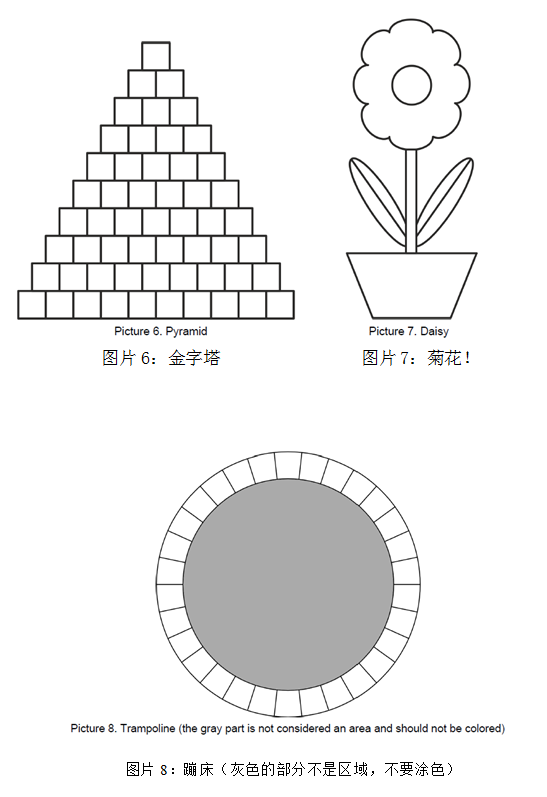
题解

这题算的久，码的短
好好算，其实不难，注意一些细节

代码

 1 #include <cstdio>
 2 #define ll long long
 3 using namespace std;
 4 const int a[8][2]={{2,1572858},{0,96},{2,18},{2,24576-6},{0,12},{0,6},{0,96},{2,1073741826-6}};
 5 int n,k;
 6 int main()
 7 {
 8     freopen("color.in","r",stdin),freopen("color.out","w",stdout),scanf("%d%d",&n,&k);
 9     int x=k*(k-1)/2,y=k*(k-1)*(k-2)/6;
10     printf("%lld\n",(ll)x*a[n-1][0]+(ll)y*a[n-1][1]);
11     return 0;
12 }