AI 梯度下降

梯度下降（gradient descent），是一种用于最优化（通常是最小化），代价函数/损失函数/目标函数/误差函数/准则，的方法。 不过，最值有时很难找到，尤其是在高维情况下，所以常常把局部最优解看作全局最优解。

1、导数

f(x)在x处的斜率。

 

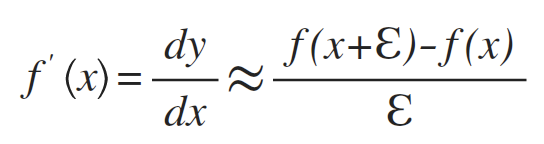
2、临界点（critical point）/驻点（stationary point）

导数为0，包括局部极小点、局部极大点、鞍点。 

 

3、偏导数（partial derivative）

f(x)关于多维输入x的其中一维xi的导数。 

 

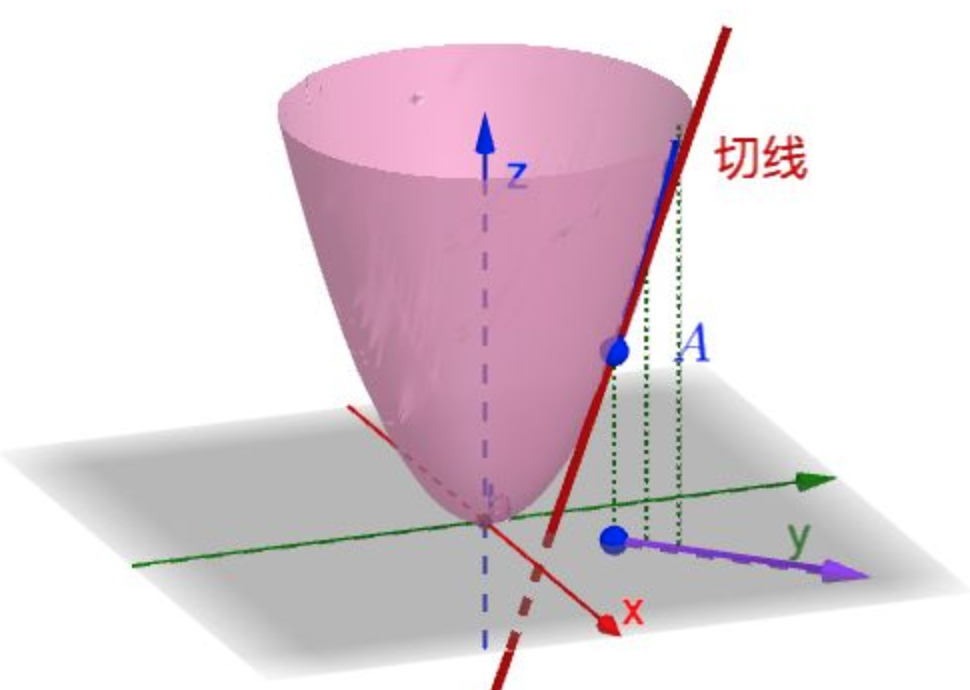
4、方向导数（directional derivative）

导数和偏导数只能描述坐标轴方向的变化率。但是一个点在无数个方向上都有变化率，这时候就需要方向导数了：f(x)在某个向量方向上的导数。

 

5、梯度

梯度是一个向量，向量的第i个元素是f(x)关于xi的偏导数。临界点是梯度中所有元素都为0的点。

 

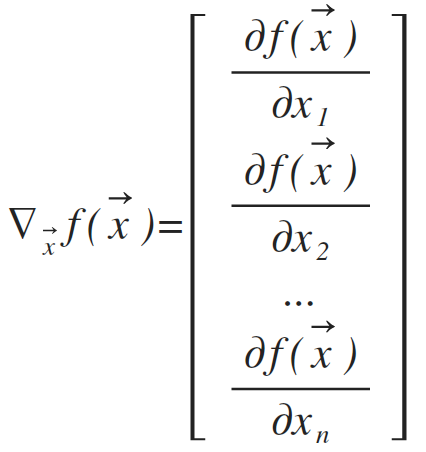
6、学习率（learning rate）

 

爬山算法

 

参考链接：

https://www.zhihu.com/question/36301367

https://zhuanlan.zhihu.com/p/38525412 

https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247483704&idx=1&sn=8f0c6e33ef84c26823e562be16bce684&chksm=ebb439ecdcc3b0fa4e9571deb33ccea62e42034c88db4e190633588307dce4a1e0c91ed2635c&scene=21#wechat_redirect 

 

转载于:https://www.cnblogs.com/yangwenhuan/p/9695807.html