Chessboard
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 9946 | Accepted: 3072 |
Description
Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below).
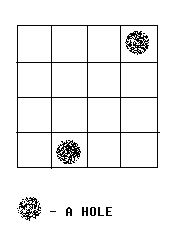
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:
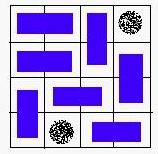
A VALID solution.
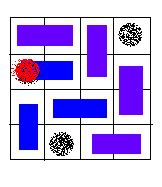
An invalid solution, because the hole of red color is covered with a card.
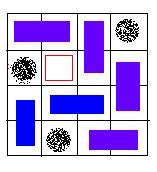
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:

A VALID solution.

An invalid solution, because the hole of red color is covered with a card.

An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.
Input
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.
Output
If the board can be covered, output "YES". Otherwise, output "NO".
Sample Input
4 3 2 2 1 3 3
Sample Output
YES
Hint
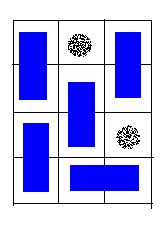
A possible solution for the sample input.
还是二分图
可以用最简单的方法来做
但是我想试着用完全匹配来做,wa了 回头再想想为什么
对错的代码都先贴着
#include<iostream> using namespace std; int input[35][35]; int map[1200][1200]; int mark[1200]; int father[1200]; int n, m; struct node { int x, y; }; node list[1200]; int num; int dfs(int a) { for(int i=1; i<=num;i++) { if(mark[i]==0 && map[a][i]==1) { mark[i]=1; if(father[i]==0 || dfs(father[i])==1) { father[i]=a; return 1; } } } return 0; } //int hung() //{ // int count=0; // memset(father, 0, sizeof(father)); // for(int i=1; i<=num;i++) // { // memset(mark, 0, sizeof(mark)); // dfs(i); // } // for(int i=1; i<=num; i++) // { // int k=father[i]; // if(k==0) // continue; // father[k]=0; // memset(mark, 0, sizeof(mark)); // map[k][i]=0; // if(dfs(k)==0) // { // count++; // father[i]=k; // } // map[k][i]=1; // } // return count; //} int hung() { memset(father, 0, sizeof(father)); int count=0; for(int i=1;i<=num;i++) { memset(mark, 0, sizeof(mark)); if(dfs(i)==1) count++; } return count; } int main() { int k; freopen("e:\\data.txt", "r", stdin); freopen("e:\\out.txt", "w", stdout); while(cin>>m>>n>>k) { memset(input, 0, sizeof(input)); for(int i=0;i<k;i++) { int a, b; cin>>a>>b; input[b][a]=1; } num=0; for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { if(input[i][j]==0) { num++; list[num].x=i; list[num].y=j; } } } memset(map, 0, sizeof(map)); for(int i=1;i<=num;i++) { for(int j=1;j<=num;j++) { if(abs(list[i].x-list[j].x)+abs(list[i].y-list[j].y)==1) { map[i][j]=1; } } } if(k%2==1) { cout<<"NO"<<endl; continue; } int res = hung()/2; if(m*n-k-res*2==0) cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0; }







 本文探讨了一种棋盘覆盖问题,即如何使用1*2大小的卡片覆盖M*N大小的棋盘,棋盘中存在一些不可覆盖的孔洞。文章提供了一个通过完全匹配算法解决该问题的具体实现方案。
本文探讨了一种棋盘覆盖问题,即如何使用1*2大小的卡片覆盖M*N大小的棋盘,棋盘中存在一些不可覆盖的孔洞。文章提供了一个通过完全匹配算法解决该问题的具体实现方案。
















 613
613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








