本文根据《大话数据结构》一书及网络资料,实现了Java版的平衡二叉树(AVL树)。
平衡二叉树介绍
在上篇博客中所实现的二叉排序树(二叉搜索树),其查找性能取决于二叉排序树的形状,当二叉排序树比较平衡时(深度与完全二叉树相同,[log2n]+1),时间复杂度为O(logn);但也有可能出现极端的斜树,如依照{35,37,47,51,58,62,73,88,91,99}的顺序,构建的二叉排序树就如下图所示,查找时间复杂度为O(n)。
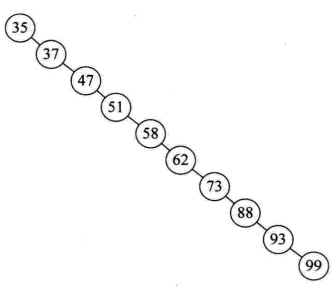
图1 斜树
为提高查找复杂度,在二叉排序树的基础上,提出了二叉平衡树:一种二叉排序树,其中每个结点的左右子树的高度差至多等于1。
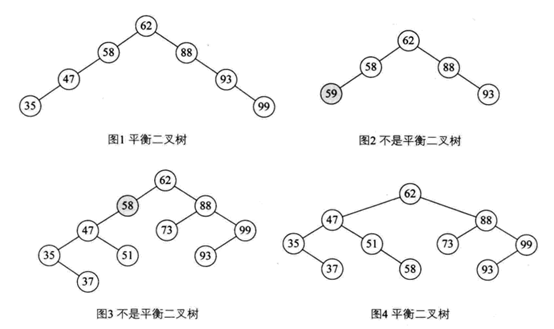
图2 平衡二叉树与非平衡二叉树
实现原理
定义二叉树结点的左子树深度减去右子树深度的值为平衡因子BF(Balance Factor),平衡树所有结点的BF只能是-1,0,1。
距离新插入结点最近,且平衡因子的绝对值大于1的结点为根的子树,称为最小不平衡子树。
构建平衡二叉树的基本思想就是:在构建过程中,每当插入一个结点时,检查是否破坏了树的平衡性,若是,则找出最小不平衡树,进行相应的调整。
具体实现步骤很多地方都有介绍,本文不再赘述。
实现算法
二叉树的结点结构定义:
private class AVLnode {
int data; // 结点数据
int bf; // 平衡因子,左高记为1,右高记为-1,平衡记为0
AVLnode lChild, rChild; // 左右孩子
public AVLnode(int data) {
this.data = data;
bf = 0;
lChild = null;
rChild = null;
}
}
根据之前提到的基本思想,为调整最小不平衡树,首先要了解两种最基本的操作:左旋操作和右旋操作。
基本操作(左/右旋操作)
(1)右旋
如下图中左边的最小不平衡二叉树,进行右旋操作即可变为右边中的平衡二叉树。
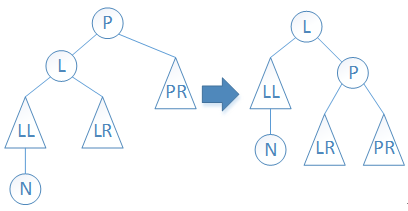
图3 右旋操作(情况1)
根据上图,容易编写右旋操作的代码如下:
/*
* 右旋
* 返回新的根结点
*/
public AVLnode rRotate(AVLnode p) {
AVLnode l = p.lChild;
p.lChild = l.rChild;
l.rChild = p;
return l;
}
(2)左旋操作
同上所述,左旋操作的图示及代码,如下所示。
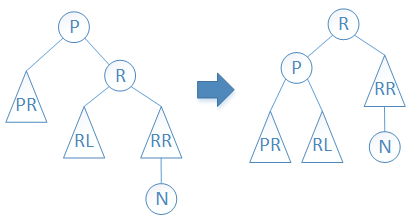
图4 左旋操作
/*
* 左旋
* 返回新的根结点
*/
public AVLnode lRotate(AVLnode p) {
AVLnode r = p.rChild;
p.rChild = r.lChild;
r.lChild = p;
return r;
}
左/右平衡旋转
对于最小不平衡子树,若其左子树深度比右子树大2(下面称为左斜的不平衡树),需进行左平衡旋转操作。若右子树深度大,则需进行右平衡旋转操作。
(1)左平衡旋转:
左斜的不平衡树有几种形式,下面分开讨论
>> L结点的BF值为1时
直接对根结点P右旋即可
情况(1):如下图所示,右旋根结点P。平衡后,P结点的BF值为0,其左结点L的BF值也为0。
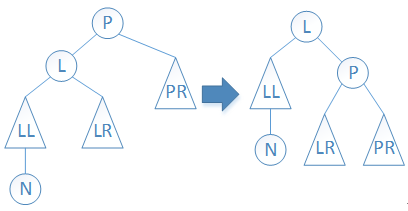
图5 情况(1)
>> L结点的BF值为-1时
都是先对L结点左旋,再对P结点右旋。根据平衡后P结点和L结点的BF值不同,可以分出下面三种情况:
情况(2):如下图所示,先左旋L结点,再右旋P结点。平衡后,P结点的BF值为-1,L结点的BF值为0,LR结点的BF值为0。
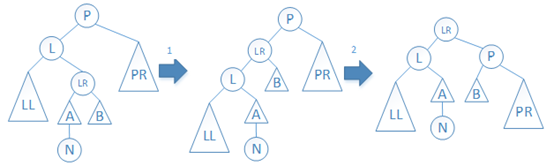
图6 情况(2)
(注:示意图中,小三角形表示的子树比大三角形表示的子树深度少1,下同)
情况(3):如下图所示,先左旋L结点,再右旋P结点。平衡后,P结点的BF值为0,L结点的BF值为1,LR结点的BF值为0。
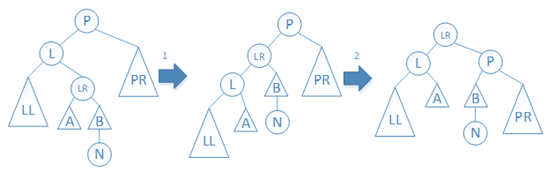
图7 情况(3)
情况(4):如下图所示,先左旋L结点,再右旋P结点。平衡后,P结点的BF值为0,L结点的BF值为0,LR结点的BF值为0。
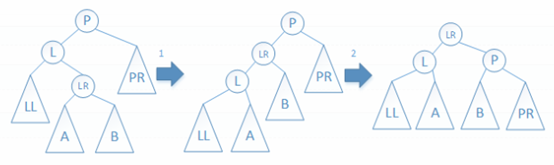
图8 情况(4)
>> L结点的BF值为0时
最小不平衡子树也可能出现下面这种情况(插入时不会出现,但删除操作过程中可能出现),《大话》一书中没有讨论到这种情况。
情况(5):如下图所示,直接右旋P结点。平衡后,L结点的BF值为-1,LR结点的BF值为1。
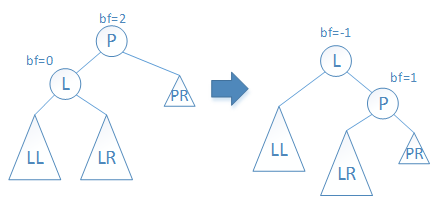
图9 情况(5)
综上所述,左平衡旋转一共可能出现5种情况,以下为左平衡旋转操作的代码:
/*
* 左平衡旋转(左子树高度比右子树高2时(左斜)执行的操作)
* 返回值为新的根结点
*/
public AVLnode leftBalance(AVLnode p) {
AVLnode l = p.lChild;
switch (l.bf) {
case 1: // 情況(1)
p.bf = 0;
l.bf = 0;
return rRotate(p);
case -1:
AVLnode lr = l.rChild;
switch (lr.bf) {
case 1: // 情況(2)
p.bf = -1;
l.bf = 0;
break; // break别漏写了
case -1: // 情況(3)
p.bf = 0;
l.bf = 1;
break;
case 0: // 情況(4)
p.bf = 0;
l.bf = 0;
break;
}
lr.bf = 0;
// 设置好平衡因子bf后,先左旋
p.lChild = lRotate(l);// 不能用l=leftBalance(l);
// 再右旋
return rRotate(p);
case 0: // 这种情况书中没有考虑到,情况(5)
l.bf = -1;
p.bf = 1;
return rRotate(p);
}
// 以下情况应该是不会出现的,所有情况都已经包括,除非程序还有问题
System.out.println("bf超出范围,请检查程序!");
return p;
}
(2)右平衡旋转:
与左平衡的分析类似,也可以分为五种情况,不再赘述,下面直接给出代码:
/*
* 右平衡旋转(右子树高度比左子树高2时执行的操作)
* 返回值为新的根结点
*/
public AVLnode rightBalance(AVLnode p) {
AVLnode r = p.rChild;
switch (r.bf) {
case -1:
p.bf = 0;
r.bf = 0;
return lRotate(p);
case 1:
AVLnode rl = r.lChild;
switch (rl.bf) {
case 1:
r.bf = -1;
p.bf = 0;
break;
case -1:
r.bf = 0;
p.bf = 1;
break;
case 0:
r.bf = 0;
p.bf = 0;
break;
}
rl.bf = 0;
p.rChild = rRotate(r);
return lRotate(p);
case 0:
p.bf = -1;
r.bf = 1;
return lRotate(p);
}
// 以下情况应该是不会出现的,所有情况都已经包括,除非程序还有问题
System.out.println("bf超出范围,请检查程序!");
return p;
}
插入操作的主函数
二叉平衡树是一种二叉排序树,所以其操作与二叉排序树相同,但为了保持平衡,需要对平衡度进行分析。
引入一个变量taller来衡量子树是否长高,若子树长高了,就必须对平衡度进行分析:如果不平衡,就进行上面所说的左右平衡旋转操作。
具体的Java实现代码如下:
/*
* 插入操作
* 要多定义一个taller变量
*/
boolean taller;// 树是否长高
public void insert(int key) {
root = insert(root, key);
}
private AVLnode insert(AVLnode tree, int key) {// 二叉查找树的插入操作一样,但多了树是否长高的判断(树没长高就完全类似BST二叉树),要记得每次对taller赋值
if (tree == null) {
taller = true;
return new AVLnode(key);
}
if (key == tree.data) {
System.out.println("数据重复,无法插入!");
taller = false;
return tree;
} else if (key < tree.data) {
tree.lChild = insert(tree.lChild, key);
if (taller == true) { // 左子树长高了,要对tree的平衡度分析
switch (tree.bf) {
case 1: // 原本左子树比右子树高,需要左平衡处理
taller = false; // 左平衡处理,高度没有增加
return leftBalance(tree);
case 0: // 原本左右子树等高,现因左子树增高而增高
tree.bf = 1;
taller = true;
return tree;
case -1: // 原本右子树比左子树高,现左右子树相等
tree.bf = 0;
taller = false;
return tree;
}
}
} else if (key > tree.data) {
tree.rChild = insert(tree.rChild, key);
if (taller == true) { // 右子树长高了,要对tree的平衡度分析
switch (tree.bf) {
case 1: // 原本左子树高,现等高
tree.bf = 0;
taller = false;
return tree;
case 0: // 原本等高,现右边增高了
tree.bf = -1;
taller = true;
return tree;
case -1: // 原本右子树高,需右平衡处理
taller = false;
return rightBalance(tree);
}
}
}
return tree;
}
AVL树的完整代码
AVL树的完整代码如下(含测试代码):
package AVLTree;
/**
* AVL树
* @author Yongh
*
*/
public class AVLTree {
private AVLnode root;
private class AVLnode {
int data; // 结点数据
int bf; // 平衡因子,左高记为1,右高记为-1,平衡记为0
AVLnode lChild, rChild; // 左右孩子
public AVLnode(int data) {
this.data = data;
bf = 0;
lChild = null;
rChild = null;
}
}
/*
* 右旋
* 返回新的根结点
*/
public AVLnode rRotate(AVLnode p) {
AVLnode l = p.lChild;
p.lChild = l.rChild;
l.rChild = p;
return l;
}
/*
* 左旋
* 返回新的根结点
*/
public AVLnode lRotate(AVLnode p) {
AVLnode r = p.rChild;
p.rChild = r.lChild;
r.lChild = p;
return r;
}
/*
* 左平衡旋转(左子树高度比右子树高2时(左斜)执行的操作)
* 返回值为新的根结点
*/
public AVLnode leftBalance(AVLnode p) {
AVLnode l = p.lChild;
switch (l.bf) {
case 1: // 情況(1)
p.bf = 0;
l.bf = 0;
return rRotate(p);
case -1:
AVLnode lr = l.rChild;
switch (lr.bf) {
case 1: // 情況(2)
p.bf = -1;
l.bf = 0;
break; // break别漏写了
case -1: // 情況(3)
p.bf = 0;
l.bf = 1;
break;
case 0: // 情況(4)
p.bf = 0;
l.bf = 0;
break;
}
lr.bf = 0;
// 设置好平衡因子bf后,先左旋
p.lChild = lRotate(l);// 不能用l=leftBalance(l);
// 再右旋
return rRotate(p);
case 0: // 这种情况书中没有考虑到,情况(5)
l.bf = -1;
p.bf = 1;
return rRotate(p);
}
// 以下情况应该是不会出现的,所有情况都已经包括,除非程序还有问题
System.out.println("bf超出范围,请检查程序!");
return p;
}
/*
* 右平衡旋转(右子树高度比左子树高2时执行的操作)
* 返回值为新的根结点
*/
public AVLnode rightBalance(AVLnode p) {
AVLnode r = p.rChild;
switch (r.bf) {
case -1:
p.bf = 0;
r.bf = 0;
return lRotate(p);
case 1:
AVLnode rl = r.lChild;
switch (rl.bf) {
case 1:
r.bf = -1;
p.bf = 0;
break;
case -1:
r.bf = 0;
p.bf = 1;
break;
case 0:
r.bf = 0;
p.bf = 0;
break;
}
rl.bf = 0;
p.rChild = rRotate(r);
return lRotate(p);
case 0:
p.bf = -1;
r.bf = 1;
return lRotate(p);
}
// 以下情况应该是不会出现的,所有情况都已经包括,除非程序还有问题
System.out.println("bf超出范围,请检查程序!");
return p;
}
/*
* 插入操作
* 要多定义一个taller变量
*/
boolean taller;// 树是否长高
public void insert(int key) {
root = insert(root, key);
}
private AVLnode insert(AVLnode tree, int key) {// 二叉查找树的插入操作一样,但多了树是否长高的判断(树没长高就完全类似BST二叉树),要记得每次对taller赋值
if (tree == null) {
taller = true;
return new AVLnode(key);
}
if (key == tree.data) {
System.out.println("数据重复,无法插入!");
taller = false;
return tree;
} else if (key < tree.data) {
tree.lChild = insert(tree.lChild, key);
if (taller == true) { // 左子树长高了,要对tree的平衡度分析
switch (tree.bf) {
case 1: // 原本左子树比右子树高,需要左平衡处理
taller = false; // 左平衡处理,高度没有增加
return leftBalance(tree);
case 0: // 原本左右子树等高,现因左子树增高而增高
tree.bf = 1;
taller = true;
return tree;
case -1: // 原本右子树比左子树高,现左右子树相等
tree.bf = 0;
taller = false;
return tree;
}
}
} else if (key > tree.data) {
tree.rChild = insert(tree.rChild, key);
if (taller == true) { // 右子树长高了,要对tree的平衡度分析
switch (tree.bf) {
case 1: // 原本左子树高,现等高
tree.bf = 0;
taller = false;
return tree;
case 0: // 原本等高,现右边增高了
tree.bf = -1;
taller = true;
return tree;
case -1: // 原本右子树高,需右平衡处理
taller = false;
return rightBalance(tree);
}
}
}
return tree;
}
/*
* 前序遍历
*/
public void preOrder() {
preOrderTraverse(root);
System.out.println();
}
private void preOrderTraverse(AVLnode node) {
if (node == null)
return;
System.out.print(node.data+" ");
preOrderTraverse(node.lChild);
preOrderTraverse(node.rChild);
}
/*
* 中序遍历
*/
public void inOrder() {
inOrderTraverse(root);
System.out.println();
}
private void inOrderTraverse(AVLnode node) {
if (node == null)
return;
inOrderTraverse(node.lChild);
System.out.print(node.data+" ");
inOrderTraverse(node.rChild);
}
/*
* 测试代码
*/
public static void main(String[] args) {
AVLTree aTree = new AVLTree();
int[] arr = { 3, 2, 1, 4, 5, 6, 7, 10, 9, 8 };
for (int i : arr) {
aTree.insert(i);
}
System.out.print("前序遍历结果:");
aTree.preOrder();
System.out.print("中序遍历结果:");
aTree.inOrder();
AVLTree bTree = new AVLTree();
int[] arr2 = { 3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9 };
for (int i : arr2) {
bTree.insert(i);
}
System.out.print("前序遍历结果:");
bTree.preOrder();
System.out.print("中序遍历结果:");
bTree.inOrder();
}
}


前序遍历结果:4 2 1 3 7 6 5 9 8 10 中序遍历结果:1 2 3 4 5 6 7 8 9 10 前序遍历结果:7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16 中序遍历结果:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
测试代码中的两个AVL树如下图所示:
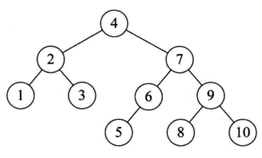
图10 aTree
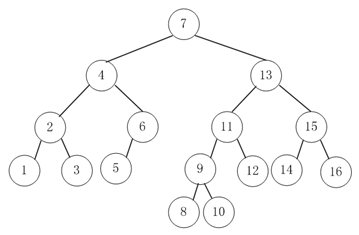
图11 bTree
后记
如果不用平衡因子BF,而是子树的高度来进行分析,讨论的情况就比较少,可参考这篇博客:AVL树(三)之 Java的实现







 本文基于《大话数据结构》一书及网络资源,详细介绍了如何使用Java实现AVL树(平衡二叉树)。文章涵盖了AVL树的基本概念、平衡因子的定义、左旋与右旋操作、平衡旋转策略及完整的Java代码实现。
本文基于《大话数据结构》一书及网络资源,详细介绍了如何使用Java实现AVL树(平衡二叉树)。文章涵盖了AVL树的基本概念、平衡因子的定义、左旋与右旋操作、平衡旋转策略及完整的Java代码实现。
















 1385
1385

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








