Dijkstra算法

最新推荐文章于 2020-10-16 20:55:42 发布

转载最新推荐文章于 2020-10-16 20:55:42 发布 · 84 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Soul-ice-ACM/articles/2140221.html

文章标签：

#c/c++ #数据结构与算法

Dijkstra算法又称为单源最短路径，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最短路径问题。
      设G=（V，E）是一个有向图，V表示顶点，E表示边。它的每一条边（i，j）属于E，都有一个非负权W（I,j），在G中指定一个结点v0，要求把从v0到G的每一个接vj（vj属于V）的最短有向路径找出来（或者指出不存在）。
      Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离
基本思想是：
      设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。
基本步骤：
1、把所有结点分成两组：
      第一组：包括已经确定最短路径的结点；
      第二组：包括尚未确定最短路径的结点。
2、开始时，第一组只包含起点，第二组包含剩余的点；
3、用贪心的策略，按最短路径长度递增的顺序把第二组的结点加到第一组去，直到v0可达的所有结点都包含于第一组中。在这个过程中，不断更新最短路径，总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。
4、每个结点对应一个距离值，第一组结点对应的距离就是v0到此结点的最短路径长度，第二组结点对应的距离值就是v0由第一组结点到此结点的最短路径长度。
5、直到所有的顶点都扫描完毕（v0可达的所有结点都包含于第一组中），找到v0到其它各点的所有最短路径。

动画演示：http://www.jcc.jx.cn/kejiandb/Dijkstra.swf

如图：求0点到其他点的最短路径。

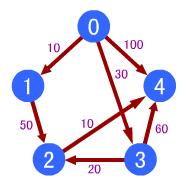
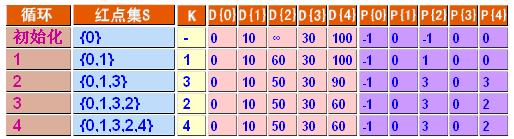
(1)开始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中，最短路径为v1，因此s1={v0,v1},由于v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中，最短路径为v3，因此s1={v0,v1,v3},由于v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；
(4)在还未进入s1的顶点之中，最短路径为v2，因此s1={v0,v1,v3,v2},由于v2到v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,60};
数据结构：
(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离，10000表示无通路：
(2)用数组dist[i..j]表示最短路径；
(3)用集合s表示找到最短路径的结点。

   1 //单源最短路（dijkstra算法）
 2program dijkstra;
 3const max=10000;    //表示无通路
 4type jihe=set of 0..100;  //顶点数
 5var
 6   a:array[0..100,0..100] of integer;//各点之间的距离
 7   dist:array[0..100] of integer; //最短路径
 8   i,j,k,m,n:integer;
 9   s:jihe;
10
11procedure init;
12begin
13   s:=[0];    //开始集合只包含源点
14   readln(n);
15   assign(input,'dijs.in');reset(input);
16   for i:=0 to n do    //读入各点之间的距离
17      for j:=0 to n do
18         read(a[i,j]);
19   for i:=0 to n do    //源点到各点之间的直接距离
20      dist[i]:=a[0,i];
21end;
22
23procedure dijsk;
24begin
25   for i:=0 to n do
26   begin
27      m:=0;
28      dist[m]:=max;  //初始化源点到各点的最小距离为无穷
29      for j:=1 to n do
30         if(not(j in s))and(dist[m]>dist[j]) then  //找出当前的最小距离
31        m:=j;    //记录找到的顶点    
32         s:=s+[m]; //把顶点加入集合
33      for k:=0 to n do    //更新经过新节点到其它点之间的最小距离
34         if(not(k in s))and(dist[k]>dist[m]+a[m,k]) then
35            dist[k]:=dist[m]+a[m,k];
36   end;
37end;
38
39begin
40   init;
41   dijsk;
42   for i:=1 to n do
43      writeln(i,':',dist[i]);
44   close(input);
45end.
 

  转：
  http://www.cnblogs.com/gzydn/archive/2009/07/09/1520019.html
 

c++实现：

/***************************************
* About:    有向图的Dijkstra算法实现
* Author:   Tanky Woo
* Blog:     www.WuTianQi.com
***************************************/

#include <iostream>
using namespace std;

const int maxnum = 100;
const int maxint = 999999;

// 各数组都从下标1开始
int dist[maxnum];     // 表示当前点到源点的最短路径长度
int prev[maxnum];     // 记录当前点的前一个结点
int c[maxnum][maxnum];   // 记录图的两点间路径长度
int n, line;             // 图的结点数和路径数
 
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
{
bool s[maxnum];    // 判断是否已存入该点到S集合中
    for(int i=1; i<=n; ++i)
    {
        dist[i] = c[v][i];
        s[i] = 0;     // 初始都未用过该点
        if(dist[i] == maxint)
            prev[i] = 0;
else
            prev[i] = v;
    }
    dist[v] = 0;
    s[v] = 1;

// 依次将未放入S集合的结点中，取dist[]最小值的结点，放入结合S中
// 一旦S包含了所有V中顶点，dist就记录了从源点到所有其他顶点之间的最短路径长度
    for(int i=2; i<=n; ++i)
    {
int tmp = maxint;
int u = v;
// 找出当前未使用的点j的dist[j]最小值
        for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
            {
                u = j;              // u保存当前邻接点中距离最小的点的号码
                tmp = dist[j];
            }
        s[u] = 1;    // 表示u点已存入S集合中

// 更新dist
        for(int j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<maxint)
            {
int newdist = dist[u] + c[u][j];
if(newdist < dist[j])
                {
                    dist[j] = newdist;
                    prev[j] = u;
                }
            }
    }
}

void searchPath(int *prev,int v, int u)
{
int que[maxnum];
int tot = 1;
    que[tot] = u;
    tot++;
int tmp = prev[u];
while(tmp != v)
    {
        que[tot] = tmp;
        tot++;
        tmp = prev[tmp];
    }
    que[tot] = v;
for(int i=tot; i>=1; --i)
if(i != 1)
            cout << que[i] << " -> ";
else
            cout << que[i] << endl;
}

int main()
{
    freopen("input.txt", "r", stdin);
// 各数组都从下标1开始

// 输入结点数
    cin >> n;
// 输入路径数
    cin >> line;
int p, q, len;          // 输入p, q两点及其路径长度

// 初始化c[][]为maxint
    for(int i=1; i<=n; ++i)
for(int j=1; j<=n; ++j)
            c[i][j] = maxint;

for(int i=1; i<=line; ++i)  
    {
        cin >> p >> q >> len;
if(len < c[p][q])       // 有重边
        {
            c[p][q] = len;      // p指向q
            c[q][p] = len;      // q指向p，这样表示无向图
        }
    }

for(int i=1; i<=n; ++i)
        dist[i] = maxint;
for(int i=1; i<=n; ++i)
    {
for(int j=1; j<=n; ++j)
            printf("%8d", c[i][j]);
        printf("\n");
    }

    Dijkstra(n, 1, dist, prev, c);

// 最短路径长度
    cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;

// 路径
    cout << "源点到最后一个顶点的路径为: ";
    searchPath(prev, 1, n);
}

输入数据:
5
7
1 2 10
1 4 30
1 5 100
2 3 50
3 5 10
4 3 20
4 5 60
输出数据:
999999 10 999999 30 100
10 999999 50 999999 999999
999999 50 999999 20 10
30 999999 20 999999 60
100 999999 10 60 999999
源点到最后一个顶点的最短路径长度: 60
源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5

最后给出两道题目练手，都是直接套用模版就OK的：
1.HDOJ 1874 畅通工程续
http://www.wutianqi.com/?p=1894

2.HDOJ 2544 最短路
http://www.wutianqi.com/?p=1892

最后给出自己第一次编的代码（很纠结啊）：

View Code

#include <stdio.h>
#include <string.h>
#define N 1010
#define MAX 0x7fffffff
int map[N][N];
int pre[N];
int dist[N];
bool s[N];
void init(int n,int line)
{
int i,j,t1,t2,len;
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
            map[i][j]=MAX;
for (i=1;i<=line;i++)
    {
        scanf("%d %d %d",&t1,&t2,&len);
if (len<map[t1][t2])
        {
            map[t1][t2]=len;
            map[t2][t1]=len;
        }
    }
for (i=1;i<=n;i++)
    {
        dist[i]=MAX;
        s[i]=0;
    }
/*输出测试
    for (i=1;i<=n;i++)
    {
        for (j=1;j<=n;j++)
            printf("%8d",map[i][j]);
        printf("\n");
    }
*/
}
void Dilk(int v,int n)
{
int i,j,temp,n_dist;
for (i=1;i<=n;i++)
    {
        dist[i]=map[v][i];
if (dist[i]==MAX)
            pre[i]=0;
else
            pre[i]=v;
    }
    dist[v]=0;
    s[v]=1;
for (i=2;i<=n;i++)
    {
        temp=MAX;
int u=v;
for (j=1;j<=n;j++)
        {
if((!s[j]) && dist[j]<temp)
            {
                u=j;
                temp=dist[j];
            }
        }
        s[u]=1;
for (j=1;j<=n;j++)
        {
if ((!s[j]) && map[u][j]<MAX)
            {
                n_dist=dist[u]+map[u][j];
if (n_dist<dist[j])
                {
                    dist[j]=n_dist;
                    pre[j]=u;
                }
            }
        }
    }
}

int main()
{
int n,m;
    scanf("%d %d",&n,&m);
    init(n,m);
    Dilk(1,n);
    printf("%d\n",dist[n]);
return 0;
}