睡前一小时数学之导数的学习与证明

最新推荐文章于 2025-08-22 07:45:16 发布

weixin_30413739

最新推荐文章于 2025-08-22 07:45:16 发布

阅读量104

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/uncle-lu/p/6016796.html

本文介绍了如何使用导数的概念来求解多项式的重根问题，并通过一个具体的编程实例展示了这一过程。文章首先解释了导数的基本概念，然后详细说明了如何利用导数判断多项式的重根。

导数：我们简单的可以理解成对于一个函数 f(X) 整体的变化趋势的一种规律。而这里的导数是一种函数。函数的导数又名导函数。

用变化率来说直白一点：设函数y=f(X) 而我们的变化率就是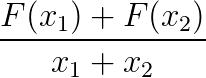这个样子的。而我们的导数，就是将变换量无限的缩小无限的缩小。无限趋近为0。用于物理来讲就是瞬时速度变化率。

说白了就是一种引入到函数里的变化率的一种概念。。

而我们这里讲解一种最基础的已知函数F(X)=Xⁿ 求出它的导函数。

恩。不对。讲之前我们还要引入一个全新的概念：二项式定理。

以下为证明过程。

已知-------式子1

假设x变化量为 Δx

可得：

将右边拆开:

可得出: 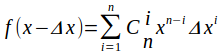-------式子2

我们之后利用之前讲过定义式

之后我们将这个式子2拆出个xⁿ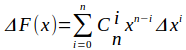

我们可以令i=0 就可得出

我们就可的出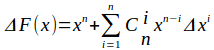-----式子3

将式子3-式子2 可得出：

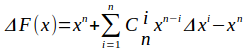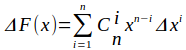===> -式4

而我们再运用定义式将式4带入：

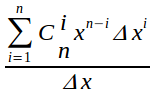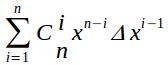==> ---式5

之后我们发现如果将Δx趋近于0 Δx的指数可以为1 其中有一项是不受Δx大小所控制的，我们将它提出。

可得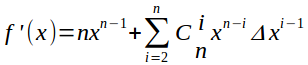----式6

我们将Δx趋近于0 可以发现。式子便可以简单的整理为

于是证明就结束了。

而多项式的导数，其实就是将每一项都求导，便可得出整个式子的导数。。

就是这样。

接下来是一道非常神奇的题目:

input:

output:

输入1：
3
-2 5 -4 1
输入2：
4
8  -20 18 -7 1
输入3：
2
2 -3 1


输出1：1 1 2
输出2：1 2 2 2

输出3 ：1 2

而这道题其实是用导数来判断重根。。题目中的解可以暴力枚举。就20个。但是重根是没有办法枚举的。。当然这道题可以用多项式除法来解决。不过。我到觉得，这个求导写起来很简单。

具体为什么能用导数求解呢？这个这里无法给出证明提供一个文献：

我们先暴力枚举出一个可行根。之后将整个多项式求导，如果这个可行根又是求导后的式子的可行根，说明这个根为重根。而我们可以继续往下将求导后的式子继续求导，继续判断是否为可行根，直到这个可行根不再是某个多阶导的可行根。就可以停止，求了几次导，就有原式中可行根这个数的几个重根。而我们就可以：以递归的形式呈现出来。之后这个实现倒是很简单。计算系数就好。

其实我个人觉得就是如果在图像中。对此函数求导后这个根的趋势，依然为0 （即趋势为没有变化），那将图像无限放大，无限放大。就可以发现。这几个根就重合在此点上。而趋势却是很小。而每一次求导就可以发现这个趋势上的趋势上的这个根的趋势。此段为本人意淫，没有什么根据。可以选择不看。

对了。还有就是。不开long long 见祖宗十年OI一场空。

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string.h>
using namespace std;
int line[10],line_1[10];
int n;
int visit[30];
int DFS(int k,int a)
{
	int step=k;
	long long int ans=0;
	for(int i=0;i<=n;++i)
	{
		if(step){
			line_1[i]*=step;
			ans+=(line_1[i]*pow(a,step-1));
			step--;
		}
		else break;
	}
	if(ans==0)
	{
		visit[a]++;
		DFS(k-1,a);
	}
	return 0;
}
int main()
{
	//freopen("equation.in","r",stdin);
	//freopen("equation.out","w",stdout);
	scanf("%d",&n);
	for(int i=n;i>=0;--i)scanf("%d",&line[i]);
	for(int a=1;a<=20;++a)
	{
		long long int  ans=0;
		int step=n;
		for(int i=0;i<=n;++i)
		{
			ans+=(line[i]*(pow(a,step)));
			step--;
		}
		if(ans==0){
			visit[a]++;
			memcpy(line_1,line,sizeof(line));
			DFS(n,a);
		}
	}
	for(int i=1;i<=20;++i)
	{
		if(visit[i])
		{
			while(visit[i]--)
			{
				printf("%d ",i);
			}
		}
	}
	//fclose(stdin);
	//fclose(stdout);
	return 0;
}

最后声明：此博客博主只是初学此内容所写下的博文。可能内有瑕疵与错误往大家指出与改正。共同学习。非常感谢。

转载于:https://www.cnblogs.com/uncle-lu/p/6016796.html