python 下的数据结构与算法---2:大O符号与常用算法和数据结构的复杂度速查表

目录：

一：大O记法

二：各函数高阶比较

三：常用算法和数据结构的复杂度速查表

四：常见的logn是怎么来的

 

一：大O记法

算法复杂度记法有很多种，其中最常用的就是Big O notation（大O记法）:

 　　

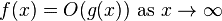
对于其中的g(x)是关于操作元素数x为自变量的计算次数函数，而x趋近无穷大从而只留下最高项且忽略其常数项是为了集中看函数随着元素个数的大量增加后运行时间的增加速度从而用来衡量时间复杂度。

e.g：

       for i in range(x):

              print(‘aha’)

              print(i)

       print(‘end’)

　　则g(x)=2x+1，留下最高项2x，去掉常数项2,最后O(x)=x

　　其他同理呐

 

二：各函数高阶比较

高阶就是函数图在第一象限更接近y轴的函数啦，常见的如下：

　　O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(n³) < O(aⁿ)

 

三：常用算法和数据结构的复杂度速查表

　　*能fanqiang的仁兄google：big O cheat sheet中的PDF就是，不能的见下图吧：

　　

　　

 

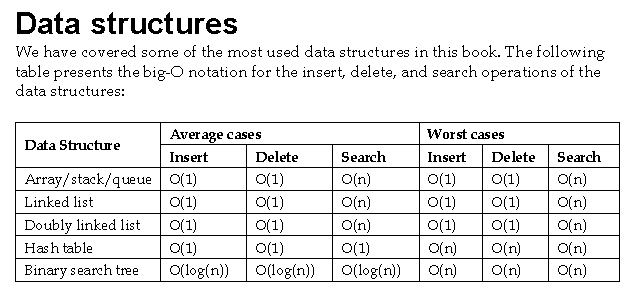
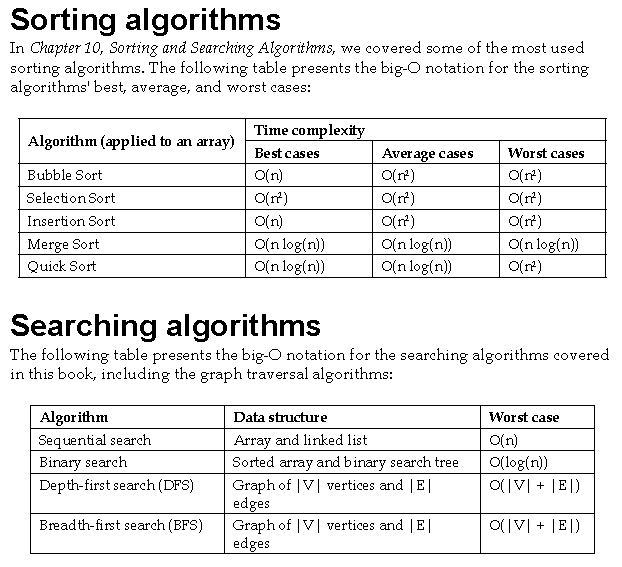
四：常见的logn是怎么来的

　　由公式：log_{b^{n = log}a}ⁿ / log_ab    (*)

　  令c = 1/log_ab

　  则（*）：log_bⁿ = c _^logaⁿ _{，而C可以省去}

　  故在如二分法等中的中的g(x)=Clog₂ⁿ可以写成logⁿ

　（即是b=2, a=10）

 

转载于:https://www.cnblogs.com/pengsixiong/p/5308919.html