WN=e^(-j*2*pi/N)
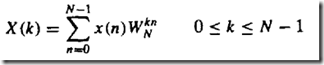
DFT复杂度o(N^2)
降低与N^2的依赖 使N = LM (L^2+m^2 <= N^2)
N点DFT分解为M段L点DFT
一维的N点序列变为(L,M)二维序列,每一行分别进行DFT
举例两种一维到二维的映射关系
n = Ml+m
| 1 | 3 | 5 | 7 | 9 |
| 2 | 4 | 6 | 8 | 10 |
n = l+mL
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
与之所求的DFT 也可存入相对应的(q,p)矩阵中
以第一种(n = Ml+m)为例:k = Mp+q
找书麻烦这里给出推到:
重一维到二维





 本文介绍了如何通过分解降低离散傅里叶变换(DFT)的时间复杂度,从O(N^2)降低到更优。通过将N点DFT分解为M段L点DFT,将一维序列转换为二维处理,详细阐述了基2 FFT算法的工作原理,解释了如何通过奇偶分离和复数乘法减少计算量。同时,举例说明了8点DFT的分解过程,并提到了二进制倒序在实现FFT中的应用。
本文介绍了如何通过分解降低离散傅里叶变换(DFT)的时间复杂度,从O(N^2)降低到更优。通过将N点DFT分解为M段L点DFT,将一维序列转换为二维处理,详细阐述了基2 FFT算法的工作原理,解释了如何通过奇偶分离和复数乘法减少计算量。同时,举例说明了8点DFT的分解过程,并提到了二进制倒序在实现FFT中的应用。
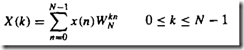
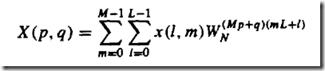
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 901
901

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








