数据处理、降维--线性判别分析(linear discriminant analysis LDA)

建议先看PCA这一节。在遇到下面的数据类型时（数据有标签，为有监督），PCA不能很好的找到一个投影方向使得变换后的数据方差最大。

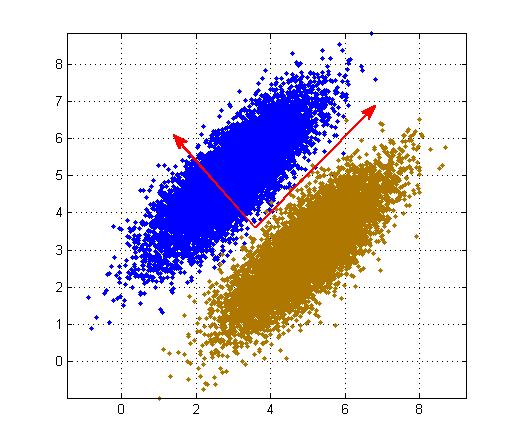
于是引入LDA。

定义原始数据集为$x = (x_{1},x_{2},,x_{n},y_{i})$，m个

样本，n个特征，i类标签（为公式简练，i=2）

设y1的数据均值为u1，对应散布矩阵为S1，y₂为u₂，S2。          下文加 ~ 表示投影以后。

目的:

投影后数据类内方差最大，类间方差最小

根据要求定义一个优化参数：

$J=\frac{\left | \widetilde{\mu _{1}}-\widetilde{\mu _{2}} \right |^{2}}{\widetilde{S_{1}^{2}}+\widetilde{S_{2}^{2}}}$

（公式复杂，照片凑数）

 

转载于:https://www.cnblogs.com/super-yb/p/11184530.html