CF450B Jzzhu and Sequences
大佬留言:这。这。不就是矩乘的模板吗,切掉它!!
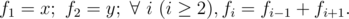 You are given xx and yy , please calculate $f_{n}(mod(10^{9}+7))$.
You are given xx and yy , please calculate $f_{n}(mod(10^{9}+7))$.
原式:$f_{i}=f_{i-1}+f_{i+1}$
转换一下:$f_{i+1}=f_{i}-f_{i-1}$
相当于$f_{i}=f_{i-1}-f_{i-2}$
有没有发现它跟斐波那契通项公式有点儿类似?
的确是这样的,那么转移矩阵也类似:
$0 -1$
$1 1$
矩阵快速幂好了
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #define LL long long #define N 10 using namespace std; class Martix{ public: LL n,m; LL A[N][N]; Martix(){ memset(A,0,sizeof(A)); } }; const LL mod=1000000007; Martix operator * (Martix A,Martix B){ Martix C; int n=A.n,m=B.m,p=A.m; C.n=n,C.m=m; for(LL i=1;i<=n;i++) for(LL j=1;j<=m;j++) for(LL k=1;k<=p;k++) C.A[i][j]=((A.A[i][k]*B.A[k][j]+mod)%mod+C.A[i][j]%mod+mod)%mod; return C; } LL x,y,n; Martix A,B; inline LL pow(){ for(;n;n>>=1,A=A*A) if(n&1) B=B*A; return B.A[1][2]; } int main() { scanf("%lld%lld%lld",&x,&y,&n); A.n=A.m=2; A.A[1][1]=0,A.A[1][2]=-1,A.A[2][1]=1,A.A[2][2]=1; B.n=1,B.m=2; B.A[1][1]=(x+mod)%mod,B.A[1][2]=(y+mod)%mod; if(n==1) printf("%lld",(x+mod)%mod); else if(n==2) printf("%lld",(y+mod)%mod); else n-=2,printf("%lld\n",pow()); return 0; }























 3056
3056

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








