概率统计
欢迎关注我的博客:http://www.cnblogs.com/xujianqing/
条件概率
设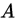 和
和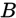 是任意两个事件,且
是任意两个事件,且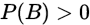 ,则称
,则称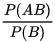 为事件
为事件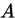 在事件
在事件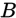 发生的条件下发生的条件概率。记作:
发生的条件下发生的条件概率。记作:
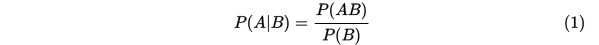
这里可以理解是,在事件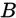 发生的情况里面去寻找事件
发生的情况里面去寻找事件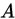 也在的例子,就是条件概率,有一种归一化的感觉,也有一种找出全局,再去挑局部的概念。
也在的例子,就是条件概率,有一种归一化的感觉,也有一种找出全局,再去挑局部的概念。
引入一个定理:
(两个事件的积的概率)=(其中一个事件的概率)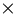 (另一个事件在前面一个事件发生条件下的条件概率)即:
(另一个事件在前面一个事件发生条件下的条件概率)即:
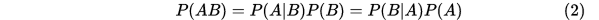
推广:
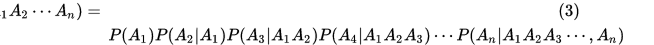
例子:


贝叶斯公式:
设 是互不相容的事件,且
是互不相容的事件,且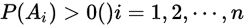 若对任意事件
若对任意事件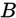 有
有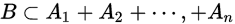 且
且 则
则
全概率公式


贝叶斯公式
其中用一个条件概率的公式
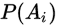 是先验概率,一般是经验的总结。
是先验概率,一般是经验的总结。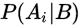 是后验概率,表示实验之后各种原因发生的可能性
是后验概率,表示实验之后各种原因发生的可能性
重复独立实验、二项概率公式
一个实验里面有两个结果,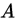 和
和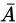 ,这个实验称为伯努利实验。它的重复n次的独立实验就叫做:n重伯努利实验。
,这个实验称为伯努利实验。它的重复n次的独立实验就叫做:n重伯努利实验。
设在每次实验中成功的概率是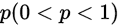 ,则在
,则在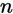 重伯努利实验中,成功恰好发生
重伯努利实验中,成功恰好发生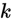 次的概率是
次的概率是
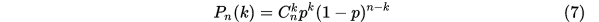
例子:

当实验次数很大的时候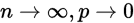 的时候,公式可变为
的时候,公式可变为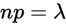 ,这时为二项泊松分布
,这时为二项泊松分布
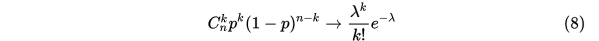
数学期望和方差
几个结论
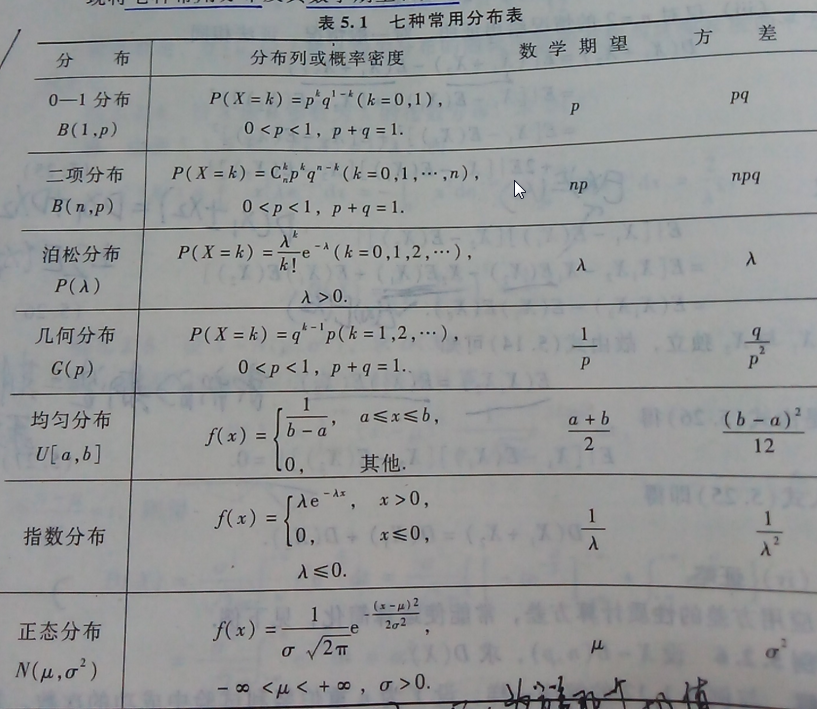
| 0-1分布 | 泊松分布 | 几何分布 | ||
|---|---|---|---|---|
| 期望 | 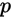 | 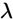 | 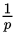 | |
| 方差 | 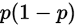 | 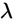 | 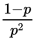 | |
切比雪夫不等式
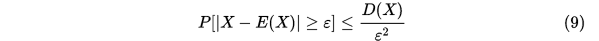
一个随机变量偏移它中心的概率是与距离和它的方差有关的不等式
伯努利大数定律
在 重伯努利实验中,成功的次数为
重伯努利实验中,成功的次数为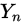 ,而每次成功的概率为
,而每次成功的概率为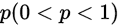 ,则对任意的
,则对任意的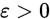 有
有
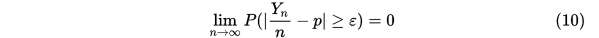
当实验次数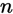 足够大的时候,成功的频率与成功的概率之差的绝对值不小于任意一个指定的正数
足够大的时候,成功的频率与成功的概率之差的绝对值不小于任意一个指定的正数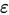 的概率可以小于任意一个预先指定的正数,这就是频率稳定性的一种确切的解释。根据伯努利大数定律在实际应用中,当实验次数
的概率可以小于任意一个预先指定的正数,这就是频率稳定性的一种确切的解释。根据伯努利大数定律在实际应用中,当实验次数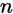 很大时,可以用事件的频率来近似得代替事件的概率。
很大时,可以用事件的频率来近似得代替事件的概率。
辛钦大数定律
设随机变量序列 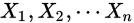 是独立同分布的随机变量,具有有限的数学期望和方差
是独立同分布的随机变量,具有有限的数学期望和方差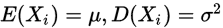 则对任意的
则对任意的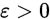 有
有
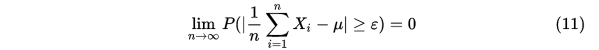
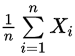 是随机变量
是随机变量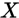 的
的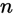 个观测值的算术平均值,而
个观测值的算术平均值,而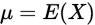 ,当实验次数足够大的时候平均值与数学期望之差的绝对值不小于任一指定的正数
,当实验次数足够大的时候平均值与数学期望之差的绝对值不小于任一指定的正数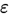 的概率小于任意一个预先指定的正数,这就是算术平均值稳定性的解释
的概率小于任意一个预先指定的正数,这就是算术平均值稳定性的解释
中心极限定理
被研究的随机变量是大量独立随机变量的和,其中每一个随机变量对于总和只起微小的作用,则可以认为这个随机变量近似服从于正态分布。
Lindeberg-levi 中心极限定理
如果随机变量序列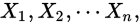 独立同分布,并且具有有限的数学期望和方差
独立同分布,并且具有有限的数学期望和方差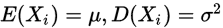 则对一切的
则对一切的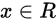
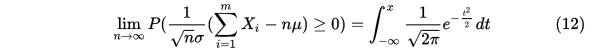
在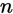 重伯努利实验中,成功的次数为
重伯努利实验中,成功的次数为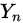 而在每次实验中成功的概率是
而在每次实验中成功的概率是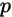 则对一切的
则对一切的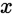 有
有
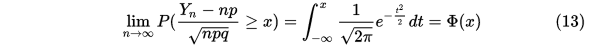




















 2887
2887

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








