BZOJ1001 [Beijing2006]狼抓兔子

最新推荐文章于 2020-04-27 20:45:05 发布

weixin_30341735

最新推荐文章于 2020-04-27 20:45:05 发布

阅读量58

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/oier/p/10003492.html

本文介绍了一种解决平面图中寻找最短路径的方法，通过将平面图转换为对偶图，再利用优先队列实现的Dijkstra算法求解最短路径。文章详细展示了代码实现过程，包括节点和边的定义、图的构建以及最短路径算法的运行。

平面图转对偶图

然后在对偶图上跑最短路即可

平面图就是指能画在二维平面上，每条边不相交的图

转对偶图

是指平面图上每一个封闭的空白区域为点

边连接的两个空白区域为新边

对于本题要稍微改一下

如图

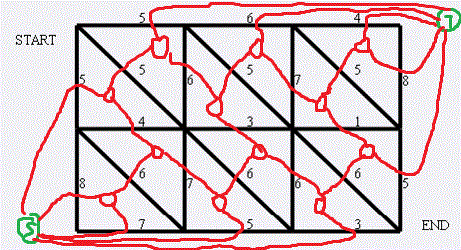
酷似17年NOIP提高组初赛题

如果对偶图的点不好用数学公式确定

可以直接给他标号啊

详见代码

#include <bits/stdc++.h>
using namespace std;

struct edge
{
    int v, w, ne;
} a[6000010];

int n, m, tot, tmp, id[1010][1010][2], src, dest, x;
int h[2000010], d[2000010];
bool v[2000010];

void add(int x, int y, int z)
{
    a[++tmp] = (edge){y, z, h[x]};
    h[x] = tmp;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i < n; i++)
        for (int j = 1; j < m; j++)
            id[i][j][0] = ++tot, id[i][j][1] = ++tot;
    src = ++tot, dest = ++tot;
    for (int i = 1; i < n; i++)
        id[i][0][1] = src, id[i][m][0] = dest;
    for (int i = 1; i < m; i++)
        id[0][i][0] = dest, id[n][i][1] = src;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j < m; j++)
            scanf("%d", &x), add(id[i - 1][j][0], id[i][j][1], x), add(id[i][j][1], id[i - 1][j][0], x);
    for (int i = 1; i < n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &x), add(id[i][j - 1][1], id[i][j][0], x), add(id[i][j][0], id[i][j - 1][1], x);
    for (int i = 1; i < n; i++)
        for (int j = 1; j < m; j++)
            scanf("%d", &x), add(id[i][j][0], id[i][j][1], x), add(id[i][j][1], id[i][j][0], x);
    priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;
    memset(d, 0x3f, sizeof(d)); d[src] = 0;
    q.push(make_pair(0, src));
    while (!q.empty())
    {
        int x = q.top().second; q.pop();
        if (v[x] == true) continue;
        v[x] = true;
        for (int i = h[x]; i != 0; i = a[i].ne)
        {
            if (v[a[i].v] == false && d[x] + a[i].w < d[a[i].v])
            {
                d[a[i].v] = d[x] + a[i].w;
                q.push(make_pair(d[a[i].v], a[i].v));
            }
        }
    }
    printf("%d\n", d[dest]);
    return 0;
}

还能用最大流最小割做

不写了太懒了QAQ

转载于:https://www.cnblogs.com/oier/p/10003492.html