四元数
圆点博士小四轴之四元数算法。四元数算法在小四轴上一般直接采用Madgwick的算法就差不多。
这是一个居于GPL的协议,大家可以自由使用。
//================
// IMU.c
// S.O.H. Madgwick
// 25th September 2010
//=================
转载如下:
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az) {
float norm;
float vx, vy, vz;
float ex, ey, ez;
// normalise the measurements
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm;
ay = ay / norm;
az = az / norm;
// estimated direction of gravity
vx = 2*(q1*q3 - q0*q2);
vy = 2*(q0*q1 + q2*q3);
vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;
// error is sum of cross product between reference direction of field and direction measured by sensor
ex = (ay*vz - az*vy);
ey = (az*vx - ax*vz);
ez = (ax*vy - ay*vx);
// integral error scaled integral gain
exInt = exInt + ex*Ki;
eyInt = eyInt + ey*Ki;
ezInt = ezInt + ez*Ki;
// adjusted gyroscope measurements
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
// integrate quaternion rate and normalise
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
// normalise quaternion
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
}
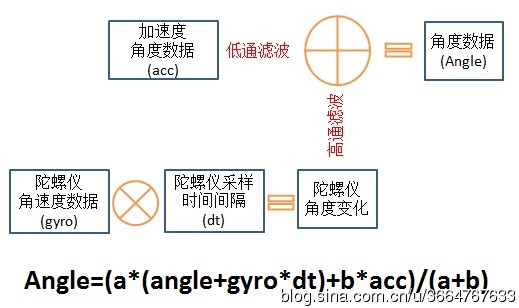
在小四轴上,我们常见的滤波方法是互补滤波。下面我们来看互补滤波是怎么工作的。
根据下图,我们可以知道,
我们每次得到的角度数据是由下列成分组成的:
1。当前的角度
2。当前陀螺仪运动所产生的角度
3。当前物体运动所产生的加速度角度
通过改变系数a和b, 我们能够调整上述各个成分的权重值,从而得到不同的滤波结果。通常我们采用a>b来进行运算。即当前的角度和陀螺仪运动产生的角度占有更大的比重,而当前加速度角度占有比较小的比重。
bs004_mpu6050_acc_pitch_com=
(bs004_filter_high*(bs004_mpu6050_acc_pitch_com+bs004_mpu6050_gyro_pitch_raw*bs004_filter_time)
+bs004_filter_low*bs004_mpu6050_acc_pitch_raw)
/(bs004_filter_high+bs004_filter_low);
bs004_mpu6050_acc_roll_com=
(bs004_filter_high*(bs004_mpu6050_acc_roll_com +bs004_mpu6050_gyro_roll_raw *bs004_filter_time)
+bs004_filter_low*bs004_mpu6050_acc_roll_raw)
/(bs004_filter_high+bs004_filter_low);























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








