bp算法中为什么会产生梯度消失？

最新推荐文章于 2024-12-19 09:13:25 发布

weixin_30316097

最新推荐文章于 2024-12-19 09:13:25 发布

阅读量133

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/DjangoBlog/p/7699592.html

本文通过数学推导详细解释了神经网络中梯度消失与梯度爆炸的问题，并介绍了LSTM解决这些问题的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

作者：维吉特伯
链接：https://www.zhihu.com/question/49812013/answer/148825073
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

简单地说，根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话（ $w_{ij}y_{i}'<1.0$ ），那么即使这个结果是0.99，在经过足够多层传播之后，误差对输入层的偏导会趋于0（ $\lim_{n\to\infty}0.99^n=0$ ）。下面是数学推导推导。

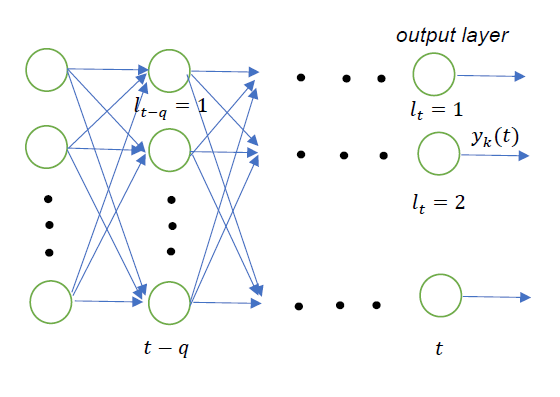
假设网络输出层中的第个神经元输出为 $y_{k}(t)$ ，而要学习的目标为 $d_{k}(t)$ 。这里的表示时序，与输入无关，可以理解为网络的第层。

&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/8930c28288aff635456f747f1802d782.png" data-rawwidth="560" data-rawheight="397" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic2.zhimg.com/v2-2fae1a385c8dcada16e17799fa175711_r.png"&gt;

若采用平方误差作为损失函数，第个输出神经元对应的损失为 $L=\frac{1}{2}(d_{k}(t)-y_{k}(t))^{2}$

将损失对输出 $y_{k}(t)$ 求偏导 $\vartheta_{k}(t)=\frac{\partial{L}}{\partial{y_{k}(t)}}=y_{k}'(t)(d_{k}(t)-y_{k}(t))$

根据链式法则，我们知道，第 t-1 层的梯度可以根据第层的梯度求出来

$\vartheta_{i}(t-1)=y_{i}'(t-1)\sum_{j}w_{ij}\vartheta_{j}(t)$

这里用表示第 t-1 层的第个神经元，表示第层的第个神经元。

进一步，第 t-q 层的梯度可以由第 t-q+1 层的梯度计算出来

$\vartheta_{i}(t-q)=y_{i}'(t-q)\sum_{j}w_{ij}\vartheta_{j}(t-q+1)$

这实际上是一个递归嵌套的式子，如果我们对 $\vartheta_{j}(t-q+1)$ 做进一步展开，可以得到式子

$\vartheta_{i}(t-q)=y_{i}'(t-q)\sum_{j}w_{ij}[y_{j}'(t-q+1)\sum_{k}w_{jk}\vartheta_{k}(t-q+2))]$

最终，可以一直展开到第层。

把所有的加法都移到最外层，可以得到

$\vartheta_{i}(t-q)=\sum_{l_{t-q+1}=1}^{n}\cdot\cdot\cdot\sum_{l_{t}=1}^{n}\prod_{m=0}^{q}w_{l_{m}l_{m-1}}\vartheta_{lm}(t-m)$

$l_{t-q+1}$ 表示的是第 t-q+1 层中神经元的下标（即第 t-q+1 层第 $l_{t-q+1}$ 个神经元）， $l_{t}$ 表示第层的下标。 m=0 对应输出层， m=q 对应第 t-q 层。实际上展开式就是从网络的第层到 t-q 层，每一层都取出一个神经元来进行排列组合的结果。这个式子并不准确，因为 m=0 时实际是损失对输出层的偏导，即