朴素集合论

1. 基本概念

• 类和元素：类是对象的一个汇集；

  符号 a∈A 的意思是对象 a 属于类 A；

2. power set（幂集）

幂集（power set）通过子集（subsets）来定义，

{x, y, z} 的全部子集（23=8）为：{}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}

则 {x, y, z} 的幂集为：{{}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}};

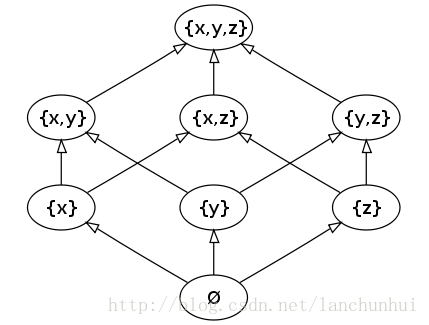
3. 集合的一个 partition

• 比如，A1,A2,…,Ak 为全集 Ω 的一个 Partition：

  需要满足一下两个性质：

  {∪ki=1Ai=Ω∩ki=1Ai=ϕ

转载于:https://www.cnblogs.com/mtcnn/p/9422492.html