算法01-最大子数组详解

最大子数组

思想：分治策略

参考书籍： 算法导论
与书籍上相比改进点：在leftsum的起始值默认包含mid 的情况下，不让right包含第一个不匹配值，解决返回造成和原理论不符合的做法，虽然在每层几个递归返回的时候比较大小可以规避这个问题，但是确实存在

注： 这里称 mid 为确认点，因为mid 不一定为中点，只是为了变成方便和效率问题。但是中点更优秀，无奈我习惯了称确认点

分治算法思想

• 分解
• 解决

• 合并

  此算法的模型如下：
  
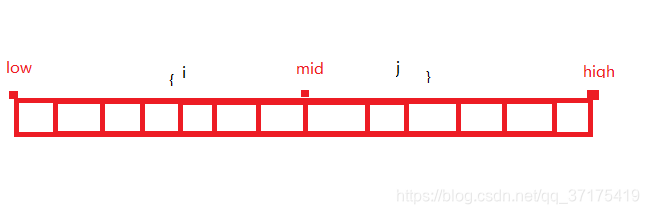
  分解 ：
  最大子数组无非三种情况：过中间一确认点、或不过这一确认点（即在三点切分的两部分）
  求解 ：
  当n =1 的时候 return 自己即(curIndex,curIndex,selfValue)。
  当n != 1的时候，就分别递归分解成小问题，直到触底（也就是不可再分割），并在每一逻辑层做判断返回该逻辑层的最优解。具体看代码 我写了详细注释的
  合并 ：
  在每层逻辑层返回给上一层的过程中，在逻辑判断下即最后的解为目的逻辑的解，即原命题最大子数组的解

• 代码如下：

//用来保存子数组下表范围，子数组和的结构体
struct rtRAndV {
    int left;
    int right;
    int value;
};

//过mid下标的最大子数组求解
rtRAndV findCrossing(int *Arr, int left, int mid, int right)
{
    rtRAndV rt;
    //注： 这里0x80000000是设置的最大负数，因为mid下标所在的位置是确定有的（不然这个求解过mid的最大数组无意义了），而mid默认包含在left部分（Arr[mid]就无论如何也能计入）。而rightsum 初始化为0，防止把无用的第一个元素带入（这里和原著不同）
    int leftsum = 0x80000000, rightsum = 0, s = 0, leftmax = mid, rightmax = mid;
    for (int i = mid; i >= left; i--)
    {
        s = s + Arr[i];
        if (s > leftsum)//第一次比较的时候就把mid 下表的数组元素给了leftsum
        {
            leftsum = s;
            leftmax = i;
        }
    }
    s = 0;
    for (int i = mid + 1; i <= right; i++)
    {
        s = s + Arr[i];
        if (s > rightsum)
        {
            rightsum = s;
            rightmax = i;
        }
    }
    //这儿直接返回 找到的范围，其实该优化一下观察是否有相同的元素的。
    rt.left = leftmax;
    rt.right = rightmax;
    rt.value = leftsum + rightsum;
    return rt;
}

//最大子数组分治 算法 递归
rtRAndV FindSubMaxArr(T *Arr, int left, int right)
{
    int mid = (right + left) / 2;
    if (left == right)
    {
        rtRAndV rt = { left,left,Arr[left] };
        return rt;
    }
    //后面这三个递归调用 的顺序无所谓，互不影响
    //这个递归是调用求解右边的最大子数组的
    rtRAndV rightsum = FindSubMaxArr(Arr, mid + 1, right);
    //递归求解左边的最大子数组
    rtRAndV leftsum = FindSubMaxArr(Arr, left, mid);
    //过确认点mid 的最大子数组
    rtRAndV cross = findCrossing(Arr, left, mid, right);
    //这里返回值的逻辑判断的顺序要留意下。如果处理不恰当，你得到的结果可能不是最优的，这就是前面的函数返回的是范围，不是元素
    //比如Arr = {5,1,-1,2,-2,-4,-2,-3} 你得到的结果是 {0,4,5}，即中间无用的和值为0的子数组也添加进去了
    //比如如下逻辑：优先选择cross造成的后果
    //if (cross.value >= leftsum.value&&cross.value >= rightsum.value)
        //return cross;
    //else if (rightsum.value >= cross.value && rightsum.value >= leftsum.value)return rightsum;
    //else return leftsum;
    //
    if (leftsum.value >= cross.value&&leftsum.value >= rightsum.value)
        return leftsum;
    else if (rightsum.value >= cross.value && rightsum.value >= leftsum.value)return rightsum;
    else return cross;

}

转载于:https://www.cnblogs.com/leibso-cy/p/Max_SubArray.html