算法——素数问题全解

最新推荐文章于 2021-01-13 18:04:55 发布

weixin_30266885

最新推荐文章于 2021-01-13 18:04:55 发布

阅读量450

点赞数

CC 4.0 BY-SA版权

文章标签： c/c++

原文链接：http://www.cnblogs.com/czc1999/p/10359443.html

1.线性素数筛（试除法）

适用范围：判定数据不大，数据量级别较小（一般超过10000就要慎重了）。

一般来说，“素数判定” 对这道题目来说只是辅助的话，用这个方法就可以过的。

int Isprime(int x) {
    //素数定义为大于1的自然数，不用考虑出现0,1负数的情况
    for (int i = 2; i <= sqrt(x); i++) {
        if (x%i == 0) return 1;
    }
    return 0;
}

题目：HDU 1262

#include <iostream>
#include <math.h>
using namespace std;
int Isprime(int x) {
    //素数定义为大于1的自然数，不用考虑出现0,1负数的情况
    for (int i = 2; i <= sqrt(x); i++) {
        if (x%i == 0) return 1;
    }
    return 0;
}
int main() {
    int x, y;
    while (cin >> x >> y) {
        if (x == 0 && y == 0)break;
        int flag = 1;
        for (int i = x; i <= y; i++) {
            int n = pow(i, 2) + i + 41; 
            if (Isprime(n)) {
                flag = 0;
                break;
            }
        }
        if (flag) cout << "OK" << endl;
        else cout << "Sorry" << endl;
    }
}

View Code

题目：HDU 2012

这题有点意思，一个偶数 N 可以分成两个距离 N/2 距离一样的素数的和。比如：20=7+13

#include <iostream>
using namespace std;

int Isprime(int x) {
    int i;
    for (i = 2; i <= sqrt(x); i++) {
        if (x%i == 0) {
            return 1;
        }
    }
    return 0;
}
int main() {
    int n;
    while (cin >> n) {
        int l, r;
        l = r = n / 2;
        while (Isprime(l) || Isprime(r))l--, r++;
        cout << l << " " << r << endl;
    }
    return 0;
}

View Code

2.埃式/欧拉筛（打表法）

适用范围：数据量级别巨大。例如：N<10^6，问N是第几个素数、输出第一百万个素数（这个更麻烦一些）

埃式筛

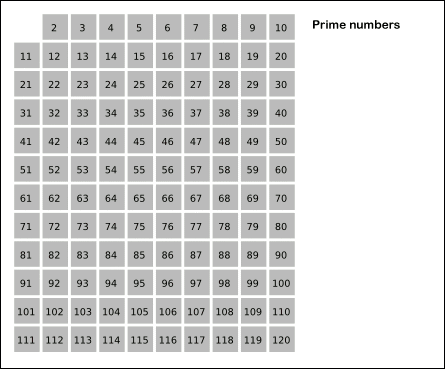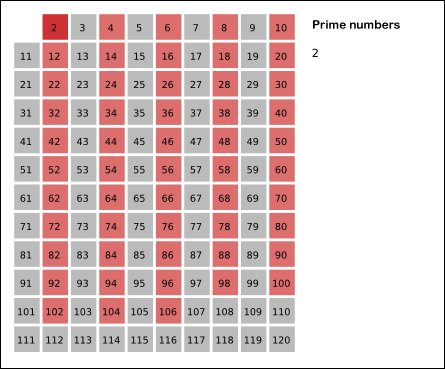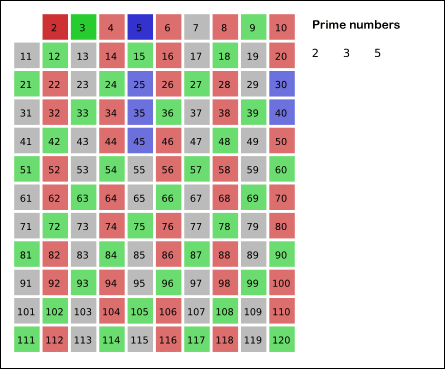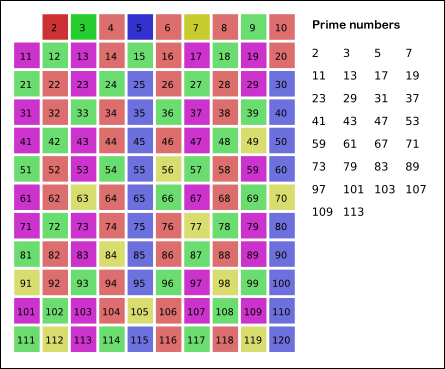
基本思想：质数的倍数一定不是质数。

void AiSieve() {
    for (int i = 2; i < N; i++) {
        if (!M[i]) {
            for (int j = i * 2; j < N; j += i) {
                M[j] = 1;
            }
        }
    }
}

欧拉筛

基本思想：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。

int M[1000001];
int prime[80000];
void EluerSieve() {
    int count = 0;
    for (int i = 2; i <= 1000000; i++){
        if (!M[i]){
            prime[count++] = i;
        }
        for (int j = 0; j < count && prime[j] * i <= 1000000; j++){
            M[i*prime[j]] = 1;
            //当 i是prime[j]的倍数时，i = k*prime[j]，如果继续 j+1，i*prime[j+1] = prime[j]*k*prime[j+1]，
　　　　　　　　//prime[j]是最小素因子，当i = k*prime[j+1]时会重复，所以跳出循环。 
            if (i%prime[j] == 0)
                break;
        }
    }
}

题目：HDU 2136

这题输出的数据级别太大了，cout 过不了。

#include <iostream>
using namespace std;

int M[1000000];

int main() {
    int count = 0;
    for (int i = 2; i < 1000000; i++) {    
        if (M[i] == 0) {
            M[i] = ++count;
            for (int j = 2 * i; j < 1000000; j+=i) {
                M[j] = count;
            }
        }
    }
    int n;
    while (scanf("%d", &n) != EOF) {
            //cout << M[n] << endl;
        printf("%d\n",M[n]);
    }
}

View Code

3.Meisell-Lehmer算法（求2...n范围内的素数个数）

这里为什么是空的呢，因为我还没看懂。

4.看脸OJ法（Miller - Rabin素数测试）

适用范围：数值特别大，（C++ 受long long数据范围限制，稳妥点只能到10^10）

原理：费马小定理_百度百科，简单来说：假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1（mod p）。反过来不一定成立。即当a^(p−1)%p=1

要做两点：

1. 打个素数表，方便取 a 的值（但要注意，a不能和p值取相同）。

2. 快速幂，问题就在这，我们要判断的数，在快速幂里是mod数，而这个mod通常很大，那么这句话 a = ((a%mod)*(a%mod)) % mod; 取余的意义其实不大，long long 十进制下19位，mod达到10位，假如正巧不巧，a正好就比mod小一点点，就可能爆范围了（我们做上百次检测，这个可能性就很大了）。

所以这个就很难受，判断大整数，还做不了太大的，就算能自己实现一个大整数，运行速度上也达不到要求了。

#include <iostream>
#include <math.h>
#include <time.h>
using namespace std;
int M[100001];
int prime[8000];
void EluerSieve() {
    int count = 0;
    for (int i = 2; i <= 100000; i++){
        if (!M[i]){
            prime[count++] = i;
        }
        for (int j = 0; j < count && prime[j] * i <= 100000; j++){
            M[i*prime[j]] = -1;
            if (i%prime[j] == 0)
                break;
        }
    }
}
int fastpower(int down,int up,int mod) {
    long long a=down, res = 1;
    while (up) {
        if (up & 1)
            res = ((res%mod)*(a%mod)) % mod;
        a = ((a%mod)*(a%mod)) % mod;
        up >>= 1;
    }
    return res;
}
int MillerRabin(int x) {
    srand(time(0));
    for (int i = 0; i < 1000; i++) {
        int a = prime[rand()%10000];
        if (a == x) {
            i--;
            continue;
        }
        if (fastpower(a, x - 1, x) != 1) {
            return 0;
        }
    }
    return 1;
}

int main() {
    int N;
    EluerSieve();
while (cin >> N) {
        //cout << M[N] << endl;
        cout << MillerRabin(N) << endl;
    }
}