[CF]Cycling City

题目大意：给定一张无向图，问图中是否存在两个点，使得这两个点之间有三条路径，而且三条路径没有公共点。

解法：

我们可以先走出来一个环，再出环上任意一点走到另外一点。就像这样：

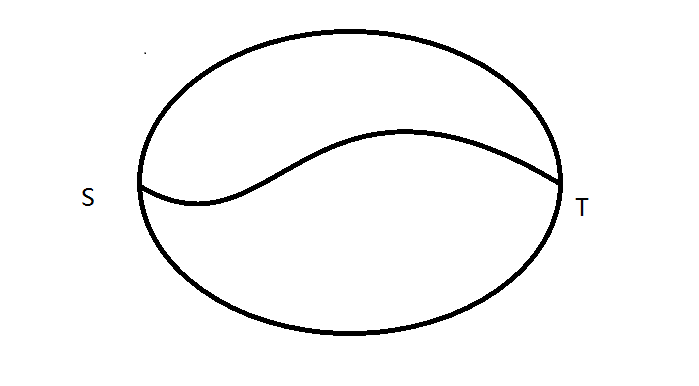
这种图有什么性质？有环。

这是什么图我们可能不知道，但是我们知道这不是什么图啊！这张图一定不是仙人掌！

然后就是如何判断仙人掌和如何输出答案的问题了

参考了这个大佬的博客，我们了解到，可以利用返祖边来判断仙人掌

显然仙人掌中的一条边不能同时出现两个环内

正如大佬所说的“如果一条树边被两条或者以上的返祖边覆盖，那么图就肯定不是一个仙人掌”

我们建出DFS树，可以发现，第一条返祖边能确定一个环，而第二条返祖边能确定三条路径的起点和终点

设起点深度小，终点深度大，我们可以发现终点是两个返祖边中深度最大的两个点的LCA

而起点则是第二条返祖边上深度最大的点与DFS树上一点相连接的一点

然后再xjbDFS一下输出路径即可代码：

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #define M 200010
  5 using namespace std;
  6 struct point{
  7     int to,next;
  8 }e[M<<1];
  9 int n,m,num,top,l1,l2,r1,r2,S,T;
 10 int ans[M],head[M],deep[M],f[M];
 11 int fa[M][20];
 12 bool vis[M];
 13 void add(int from,int to)
 14 {
 15     e[++num].next=head[from];
 16     e[num].to=to;
 17     head[from]=num;
 18 }
 19 void dfs(int x)
 20 {
 21     vis[x]=true;
 22     for(int i=head[x];i;i=e[i].next)
 23     {
 24         int to=e[i].to;
 25         if(to==fa[x][0]) continue;
 26         if(!vis[to])
 27         {
 28             deep[to]=deep[x]+1;
 29             fa[to][0]=x;
 30             dfs(to);
 31         }
 32         else if(deep[to]<deep[x])//返祖 
 33         {
 34             f[to]--;
 35             f[x]++;
 36         }
 37     }
 38     f[fa[x][0]]+=f[x];
 39 }
 40 void DFS(int x)
 41 {
 42     for(int i=head[x];i;i=e[i].next)
 43     {
 44         int to=e[i].to;
 45         if(to==fa[x][0]) continue;
 46         if(deep[to]==deep[x]+1)
 47         {
 48             DFS(to);
 49             if(l2) return;
 50         }
 51         else if(deep[to]<deep[S])//找到两条返祖边 
 52         {
 53             if(l1) r2=x,l2=to;
 54             else r1=x,l1=to;
 55             if(l2) return;
 56         }
 57     }
 58 }
 59 int lca(int x,int y)
 60 {
 61     if(deep[x]<deep[y]) swap(x,y);
 62     for(int i=18;i>=0;i--)
 63         if(deep[fa[x][i]]>=deep[y])
 64             x=fa[x][i];
 65     if(x==y) return y;
 66     for(int i=18;i>=0;i--)
 67         if(fa[x][i]!=fa[y][i])
 68         {
 69             x=fa[x][i];
 70             y=fa[y][i];
 71         }
 72     return fa[x][0]; 
 73 }
 74 int main()
 75 {
 76     scanf("%d%d",&n,&m);
 77     for(int i=1;i<=m;i++)
 78     {
 79         int x,y; scanf("%d%d",&x,&y);
 80         add(x,y); add(y,x);
 81     }
 82     for(int i=1;i<=n;i++)
 83         if(!vis[i])
 84             dfs(i);
 85     for(int i=1;i<=n;i++)
 86         if(f[i]>1)
 87         {
 88             S=i;
 89             break;
 90         }
 91     if(S==0) {printf("NO"); return 0;}
 92     printf("YES\n");
 93     DFS(S);
 94     for(int j=1;j<=18;j++)
 95         for(int i=1;i<=n;i++)
 96             fa[i][j]=fa[fa[i][j-1]][j-1];
 97     T=lca(r1,r2);
 98     if(deep[l1]<deep[l2]) swap(l1,l2),swap(r1,r2);
 99     S=l1;
100     int now=T;
101     top=0;
102     while(1)
103     {
104         ans[++top]=now;
105         if(now==S) break;
106         now=fa[now][0];
107     }
108     printf("%d ",top);
109     for(int i=top;i>=1;i--) printf("%d ",ans[i]);
110     printf("\n");
111     top=0;
112     ans[++top]=S;
113     now=r1;
114     while(1)
115     {
116         ans[++top]=now;
117         if(now==T) break;
118         now=fa[now][0];
119     }
120     printf("%d ",top);
121     for(int i=1;i<=top;i++) printf("%d ",ans[i]);
122     printf("\n");
123     top=0;
124     if(S==l2)
125     {
126         ans[++top]=S;
127         now=r2;
128         while(1)
129         {
130             ans[++top]=now;
131             if(now==T) break;
132             now=fa[now][0];
133         }
134     }
135     else
136     {
137         now=S;
138         while(1)
139         {
140             ans[++top]=now;
141             if(now==l2) break;
142             now=fa[now][0];
143         }
144         now=r2;
145         while(1)
146         {
147             ans[++top]=now;
148             if(now==T) break;
149             now=fa[now][0];
150         }
151     }
152     printf("%d ",top);
153     for(int i=1;i<=top;i++) printf("%d ",ans[i]);
154     return 0;
155 }

 

转载于:https://www.cnblogs.com/Slrslr/p/9531626.html