BFS算法详解-优快云博客

BFS的最好理解就是“层次遍历”，他是一层层往下走的。时间复杂度同DFS。

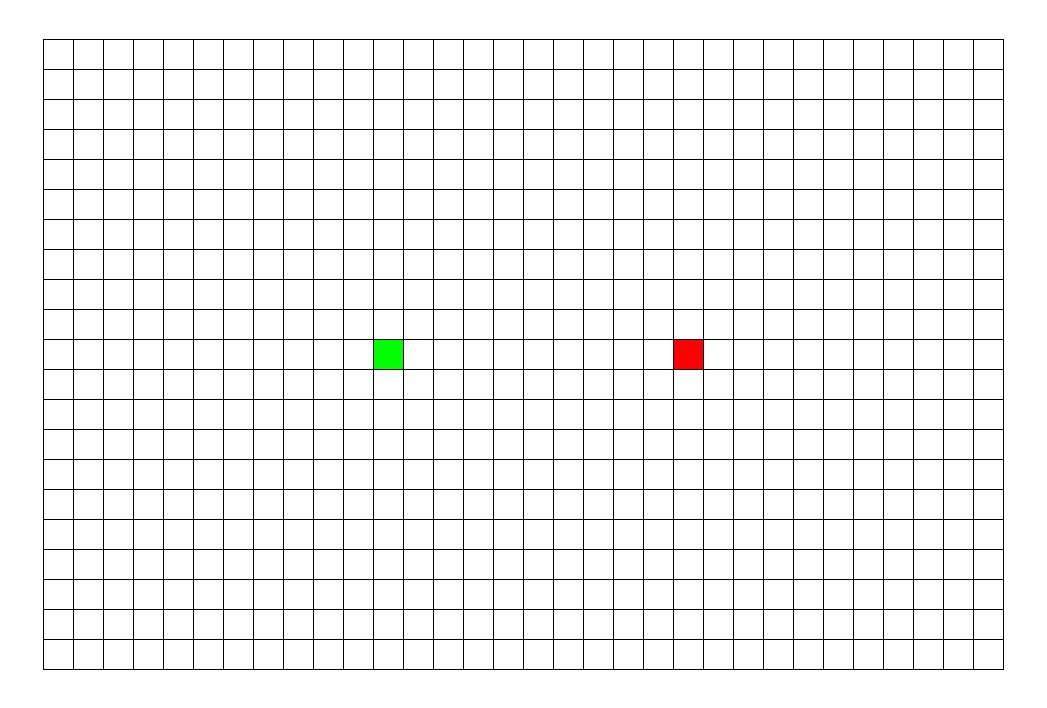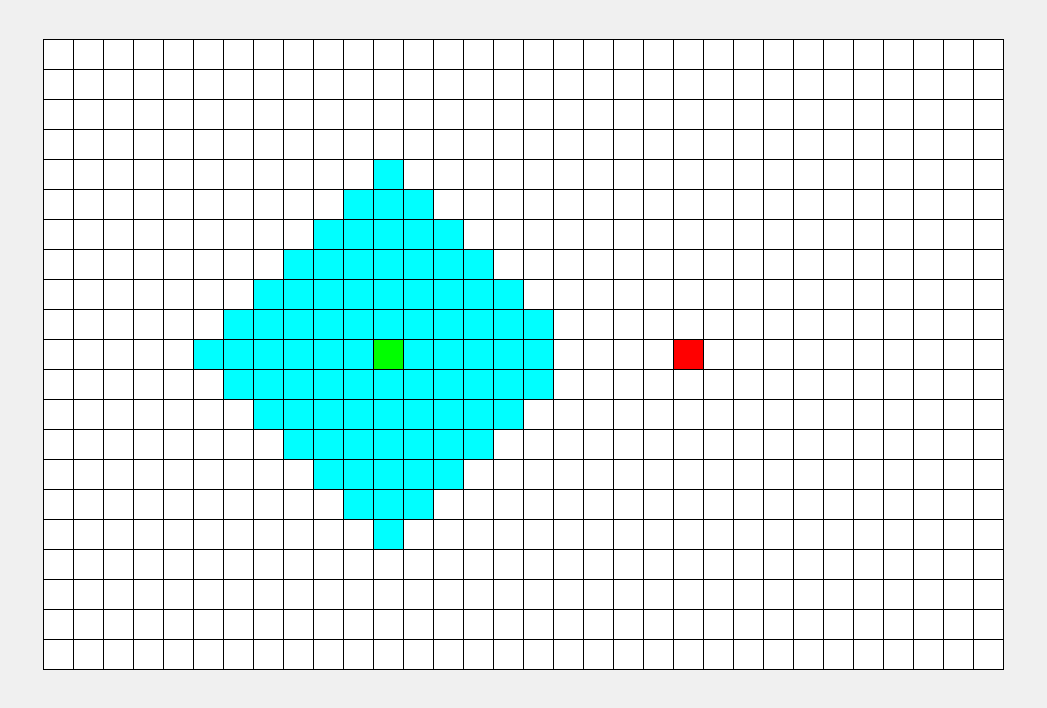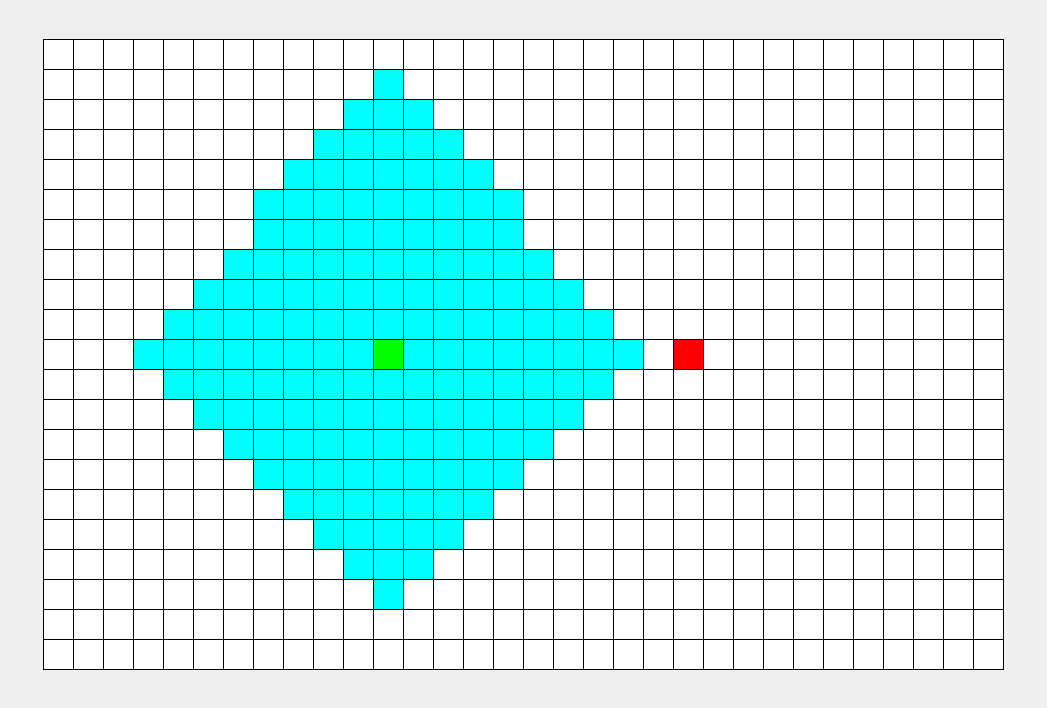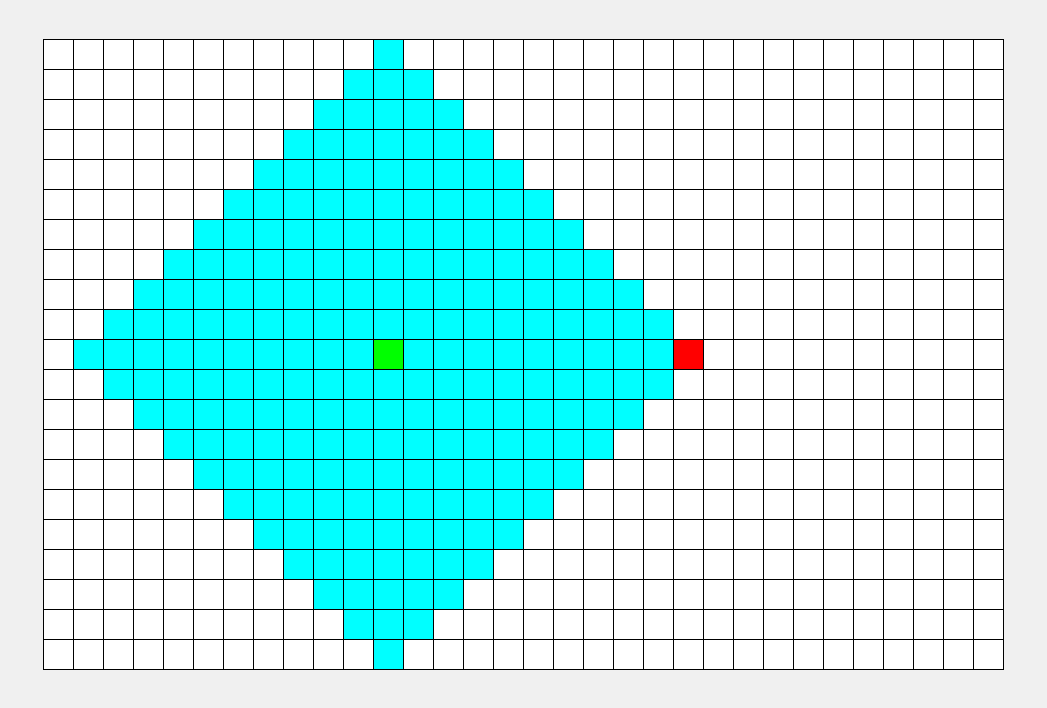
重点在于使用队列来缓存要遍历的结点。

给出核心代码（c++）：使用STL中的queue,vex[v][v_i] is adjacent matrix

 1 queue<int> que;
 2 que.push(v0); //v0是起始点 
 3 while(!que.empty()){
 4     int v = que.front(); //取队头
 5     que.pop(); //出队
 6     for(int vi=0;vi<n;vi++){
 7         if(vex[v][vi]){
 8             que.push(vi); //vi入队 
 9         }
10     }
11 }

BFS可以推广到三维数组，用于计算由像素块组成的三维不规则物体体积、三维物体的连通情况。之前在PAT题目中遇到过一次，在此特别记录一下这样题目的处理方法。

这种题目是二维BFS走迷宫过程的一种扩展。先说一下三维数组的表示以及初始化：

pixel vex[550][550][550];
for(int z=0;z<l;z++){
    for(int x=0;x<n;x++){
       for(int y=0;y<m;y++){
            vex[z][x][y].x = x;
            vex[z][x][y].y = y; 
            vex[z][x][y].z = z; 
            vex[z][x][y].state = 1;
         }
     }
}

假设v[z][x][y]=1说明这点被像素所填充，这样上面的代码就构造了n*m*l完全被填充的立方体。

再来假设搜索位上下左右前后，那么BFS的方向数组又该如何设计？

1 int x[6] = {1,0,-1,0,0,0};
2 int y[6] = {0,1,0,-1,0,0};
3 int z[6] = {0,0,0,0,1,-1};

那么接下来BFS的核心很好处理了

检验函数，可以很好的避免堆栈溢出~~

1 bool check(int z,int x,int y){
2     return tz>=0 && tz<l && tx>=0 && tx<n && ty>=0 && ty<m; 
3 }

 1 que<pixel> vex;
 2 while(!que.empty()){
 3     pixel v = que.front();
 4     que.pop();
 5     for(int i=0;i<6;i++){
 6         int tz = v.z+z[i];    //求下个点 
 7         int tx = v.x+x[i];
 8         int ty = v.y+y[i];
 9         check(tz,tx,ty) continue;
10         if( vex[tz][tx][ty] ){ //可以到达 
11             que.push(vex[tz][tx][ty]);
12         }
13     }
14 }

以上就是三维物体体积的BFS求解方式。之后再说一个个人观点，二维平面求不规则面积的问题似乎也可以用这种方式解决。

BFS在做层次遍历的时候我们要怎样记录各点所属的层呢？

 1 while(!que.empty()){
 2     vi = que.front();
 3     if(layer[vi] > maxlayer){
 4         maxlayer = layer[vi];    //BFS tree的深度
 5         index = 10010;    //初始化为极大
 6     }
 7     if(vi != v0){
 8         index = min(index,vi);    //最深那层中的编号最小的点
 9     }
10     for(int i=1;i<=n;i++){
11         if(!visit[i] && v[vi][i] != 0){
12         visit[i] = true;
13         layer[i] = layer[vi]+1;    //进入了下一层，记录下i点所在的层数
14         que.push(i);
15         }
16     }
17     que.pop();
18 }