Sparse Autoencoder Recap
In the sparse autoencoder, we had 3 layers of neurons: an input layer, a hidden layer and an output layer. In our previous description of autoencoders (and of neural networks), every neuron in the neural network used the same activation function. In these notes, we describe a modified version of the autoencoder in which some of the neurons use a different activation function. This will result in a model that is sometimes simpler to apply, and can also be more robust to variations in the parameters.
Recall that each neuron (in the output layer) computed the following:
where a(3) is the output. In the autoencoder, a(3) is our approximate reconstruction of the input x = a(1).
Because we used a sigmoid activation function for f(z(3)), we needed to constrain or scale the inputs to be in the range[0,1], since the sigmoid function outputs numbers in the range [0,1].
引入 —— 相同的activation function ,非线性映射会导致输入和输出不等
Linear Decoder
One easy fix for this problem is to set a(3) = z(3). Formally, this is achieved by having the output nodes use an activation function that's the identity function f(z) = z, so that a(3) = f(z(3)) = z(3). 输出结点不适用sigmoid 函数
This particular activation function
is called the linear activation function。Note however that in the hidden layer of the network, we still use a sigmoid (or tanh) activation function, so that the hidden unit activations are given by (say)
, where
is the sigmoid function, x is the input, and W(1) andb(1) are the weight and bias terms for the hidden units. It is only in the output layer that we use the linear activation function.
An autoencoder in this configuration--with a sigmoid (or tanh) hidden layer and a linear output layer--is called a linear decoder.
In this model, we have
. Because the output
is a now linear function of the hidden unit activations, by varying W(2), each output unit a(3) can be made to produce values greater than 1 or less than 0 as well. This allows us to train the sparse autoencoder real-valued inputs without needing to pre-scale every example to a specific range.
Since we have changed the activation function of the output units, the gradients of the output units also change. Recall that for each output unit, we had set set the error terms as follows:
where y = x is the desired output,
is the output of our autoencoder, and
is our activation function. Because in the output layer we now have f(z) = z, that implies f'(z) = 1 and thus the above now simplifies to:
output结点
Of course, when using backpropagation to compute the error terms for the hidden layer:
hidden结点
Because the hidden layer is using a sigmoid (or tanh) activation f, in the equation above
should still be the derivative of the sigmoid (or tanh) function.




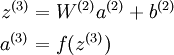
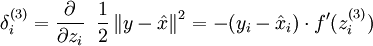
















 17
17

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








