84. Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

 

The largest rectangle is shown in the shaded area, which has area = 10 unit.

 

For example,
Given height = [2,1,5,6,2,3],
return 10.

---

这两天参加JOB Fair感觉，有些基本方法还是要先能想出来写出来，把问题解决了再去想更好的方法。

对于小数据，也许最基本的方法就可以解决问题。

这题肯定能用O(N^2)先解出来

public class Solution {
    public int largestRectangleArea(int[] height) {
        
        int maxArea = 0;
        
        for(int i=0; i<height.length; i++){
            
            int minH = height[i];
            
            for(int j=i; j<height.length; j++){
                // update min height
                if(height[j] < minH) minH=height[j];
                
                int area = (j-i+1) * minH;
                
                // update maxArea
                if(area > maxArea) maxArea = area;
            }
            
        }
        return maxArea;
    }
}

---

之后是O(N)

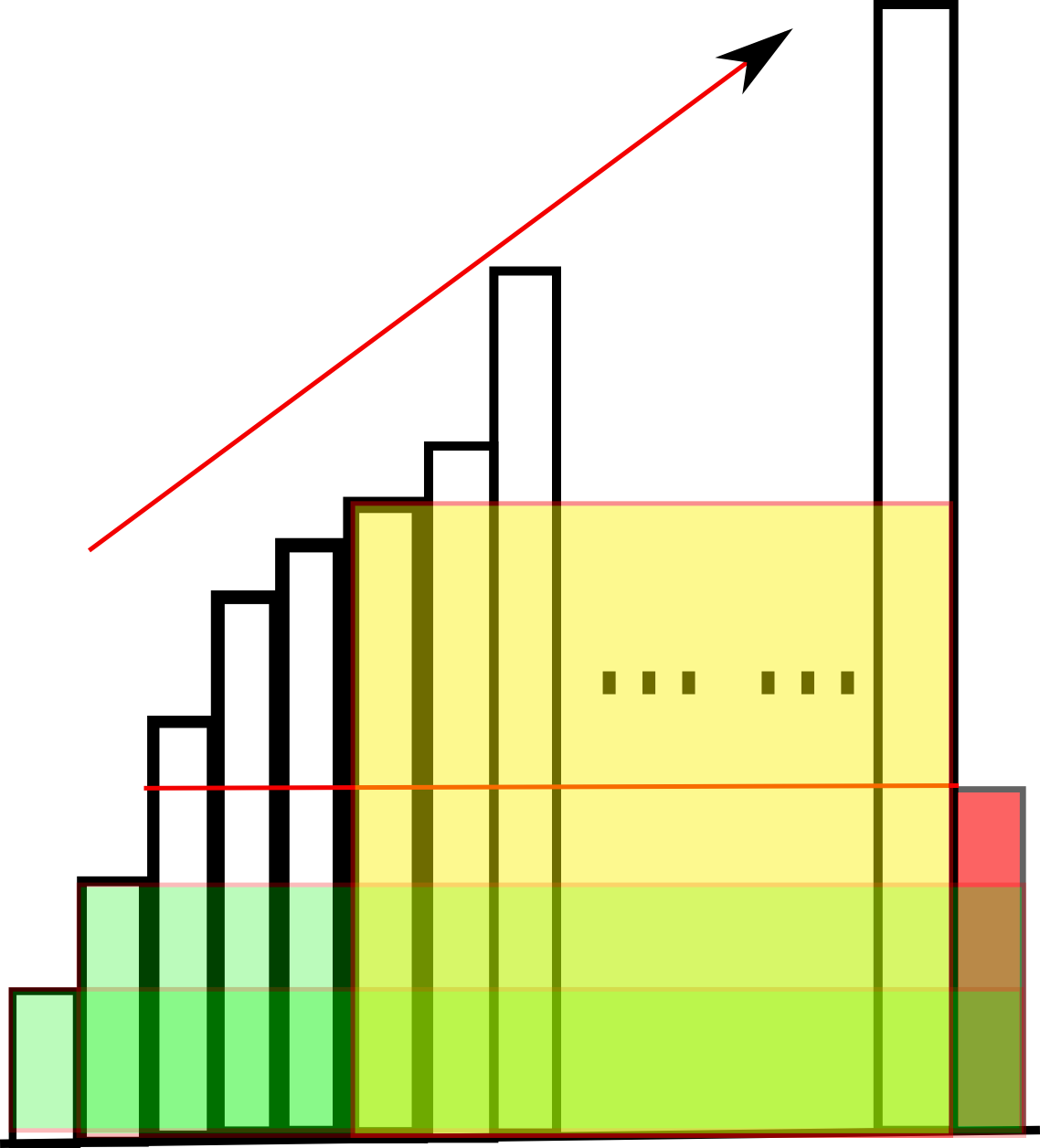
if stack空或者递增就入栈

如果出现个小的， 图中红色。 

　　- 高度位于红线上方的, 也就是不红色高的Bar，不可能和红bar围成一个比大于在弹栈过程中的矩形面积了（黄色面积

　　- 但是红色可以与黄色bar之前的bar联合， 以长度的优势，获得maxarea, 所以弹栈到比红色bar小就停止了。

注意: 弹栈过程中面积的计算。

h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1)

h[t]是刚刚弹出的栈顶端元素。

栈内索引指向的元素都是比h[t]小的，如果h[t]是目前最小的，那么栈内就是空哦。

而在目前栈顶元素和h[t]之间（不包括h[t]和栈顶元素），都是大于他们两者的。

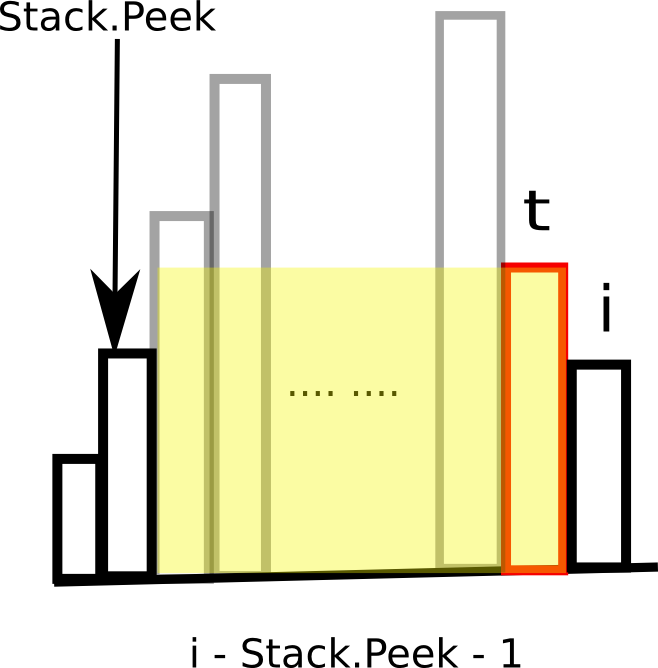
那h[t]无疑就是Stack.Peek和t之间那些上流社会的短板啦，而它们的跨越就是i - Stack.Peek - 1。 

 

10/01 YC version

copy 一个新数组，多家一个0， 太consuming

最后pop到stack empty为止就好

public class Solution {
    public int largestRectangleArea(int[] height) {
        
        int maxArea = 0;
        Stack<Integer> stack = new Stack<Integer>();
        
        int i=0;
        while(i<height.length){
            
            if(stack.isEmpty() || height[stack.peek()] <= height[i]){
                stack.push(i);
                i++;
            }else{
                // current min height index t
                int t = stack.pop();
                int area = (stack.isEmpty() ? i : i-stack.peek()-1) * height[t];
                // update
                if(area > maxArea)  maxArea = area;
            }
        }
        
        while(!stack.isEmpty()){
            int t = stack.pop();
            int area = (stack.isEmpty() ? i : i-stack.peek()-1) * height[t];
            // update
            if(area > maxArea)  maxArea = area;
        }
        
        
        return maxArea;
    }
}

 

 

---

reference

public int largestRectangleArea2(int[] height) {
        Stack<Integer> stack = new Stack<Integer>();
        int i = 0;
        int maxArea = 0;
        int[] h = new int[height.length + 1];
        h = Arrays.copyOf(height, height.length + 1);
        while(i < h.length){
            if(stack.isEmpty() || h[stack.peek()] <= h[i]){
                stack.push(i++);
            }else {
                int t = stack.pop();
                maxArea = Math.max(maxArea, h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1));
            }
        }
        return maxArea;
    }

http://www.cnblogs.com/lichen782/p/leetcode_Largest_Rectangle_in_Histogram.html

转载于:https://www.cnblogs.com/ycled/p/3330153.html