【数据结构】28、判断链表是否有环

 

因为最近小米电话面试被问到如何判断一个链表是否有环，那今天正好实现以下这个算法

1.链表

package y2019.Algorithm.LinkedList;

/**
 * @ProjectName: cutter-point
 * @Package: y2019.Algorithm.LinkedList
 * @ClassName: FindRing
 * @Author: xiaof
 * @Description: 现在存在一条链表，寻找这个链表是否存在环
 * @Date: 2019/6/24 9:12
 * @Version: 1.0
 */
public class FindRing {

    public class Node {
        private String key;
        private String value;
        private Node next;

        public String getKey() {
            return key;
        }

        public void setKey(String key) {
            this.key = key;
        }

        public String getValue() {
            return value;
        }

        public void setValue(String value) {
            this.value = value;
        }

        public Node getNext() {
            return next;
        }

        public void setNext(Node next) {
            this.next = next;
        }
    }

    //链表头结点
    private Node ringHead;
    private Node ringTail;
    private int length;

    public FindRing() {
        ringHead = ringTail = null;
    }

    //创建一个长度为n的链表
    public FindRing(int length) {
        ringHead = ringTail = null;
        Node curNode = ringHead;
        for(int i = 0; i < length; ++i) {
            if(ringHead == null) {
                ringHead = new Node();
                ringHead.key = i + " " + System.currentTimeMillis();
                curNode = ringHead;
                ringTail = curNode;
            } else if (curNode.next == null) {
                curNode.next = new Node();
                curNode = curNode.next;
                curNode.key = i + " " + System.currentTimeMillis();
                ringTail = curNode;
            }
        }
        this.length = length;
    }

    public int size() {
        return length;
    }

    public void add(Node newNode) {
        //添加节点进入链表
        //尾部插入
        if(ringTail == null) {
            ringTail = newNode;
            ringTail = ringTail.next;
        } else {
            Node temp = ringTail.next;
            temp = newNode;
            ringTail = temp.next;
        }
        ++length;
    }

    public Node getByIndex(int index) {
        Node resultNode = ringHead;
        for(int i = 1; i < index; ++i) {
            resultNode = resultNode.next;
        }
        return resultNode;
    }

    public Node getRingHead() {
        return ringHead;
    }

    public void setRingHead(Node ringHead) {
        this.ringHead = ringHead;
    }

    public Node getRingTail() {
        return ringTail;
    }

    public void setRingTail(Node ringTail) {
        this.ringTail = ringTail;
    }

    public int getLength() {
        return length;
    }

    public void setLength(int length) {
        this.length = length;
    }
}

 

内部类的使用，是为了方便调试

测试类：

package LinkedList;

import org.junit.jupiter.api.Test;
import y2019.Algorithm.LinkedList.FindRing;

import java.util.HashSet;
import java.util.Set;

/**
 * @ProjectName: cutter-point
 * @Package: LinkedList
 * @ClassName: Test1
 * @Author: xiaof
 * @Description: ${description}
 * @Date: 2019/6/24 9:31
 * @Version: 1.0
 */
public class Test1 {

    @Test
    public void test1 () {
        //判断一个链表是否有环
        //1.实现链表set方式，也就是通过hashcode进行定位
        FindRing findRing = new FindRing(15);

        //创建环节点
        int ringIndex = (int) (Math.random() * 10);
        ringIndex = 5;
        FindRing.Node ringNode = findRing.getByIndex(ringIndex);
        FindRing.Node tailNode = findRing.getRingTail();
        tailNode.setNext(ringNode);

        //开始判断是否有环
        Set set = new HashSet();
        //循环遍历链表，直到得到重复的
        FindRing.Node indexNode = findRing.getRingHead();
        int indexCount = 0;
        while(true) {
            if(indexNode == null) {
                System.out.println("无环");
                break;
            }
            if(set.contains(indexNode)) {
                System.out.println("有环,key:" + indexNode.getKey() + " 遍历次数：" + indexCount);
                break;
            }
            set.add(indexNode);
            indexNode = indexNode.getNext();
            indexCount += 1;
        }

        System.out.println("结束遍历");

    }

    @Test
    public void test2 () {
        //判断一个链表是否有环
        //1.通过2个指针同时查询，直到两个指针指向同一个节点作为有环，如果结束，那么无换
        FindRing findRing = new FindRing(15);

        //创建环节点
        int ringIndex = (int) (Math.random() * 10);
        ringIndex = 5;
        FindRing.Node ringNode = findRing.getByIndex(ringIndex);
        FindRing.Node tailNode = findRing.getRingTail();
        tailNode.setNext(ringNode);

        //开始判断是否有环
        FindRing.Node index1 = findRing.getRingHead();
        FindRing.Node index2 = findRing.getRingHead().getNext();
        int indexCount = 0;
        int indexCount2 = 0;
        //第一个每次遍历一个，第二个每次遍历2个
        while (true) {

            if(index1 == null || index2 == null || index2.getNext() == null) {
                System.out.println("无环");
                break;
            }

            if(index1 == index2) {
                System.out.println("有环,key:" + index1.getKey() + " 遍历次数1：" + indexCount + " 遍历次数2：" + indexCount2);
                break;
            }

            indexCount += 1;
            indexCount2 += 2;
            index1 = index1.getNext();
            index2 = index2.getNext().getNext();
        }

        System.out.println("结束遍历");
    }
}

 

结果：

测试一：

 

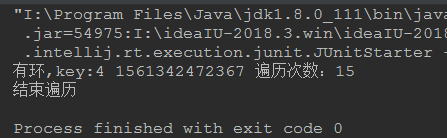
测试二：

 

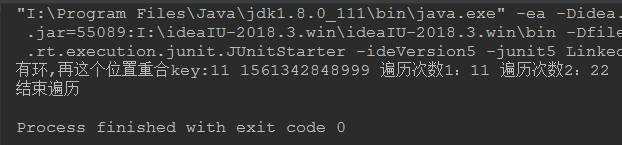
 从这里我们可以判断到第二个方法并不能定位到产生环的节点是哪个节点，并且循环次数比第一个多

总结：

方式一：对空间占用比较大，但是时间复杂度底，并且可以定位到产生环节点的位置

方式二：对空间占用比较小，但是时间复杂度高，并且无法定位到具体产生环的节点

 

转载于:https://www.cnblogs.com/cutter-point/p/11075701.html