Codeforces 337D

题意略。

思路：

本题着重考察树的直径。如果我们将这些标记点相连，将会得到大树中的一个子树。我之前只知道树内的点到直径上两端点的距离是最远的，其实，在

整个大树中，这个性质同样适用，也即大树上任意一点，到子树中任意一点的距离，其中距离最远者必为子树直径上的端点。

 

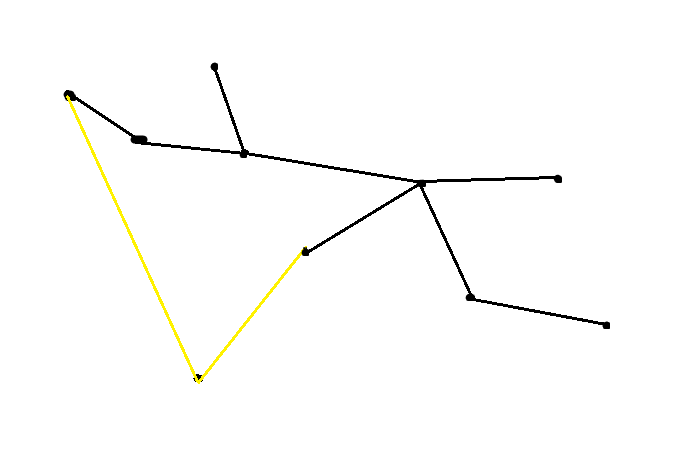
如果我从子树的端点接入，那子树中的最远点必然是端点；如果我从非端点接入，那我到最远点的距离是   我到非端点的距离 + 非端点所能达到的最远点的距离

也即我到某个端点的距离。

 

那么我只要看任一个点到子树的两个端点的距离中最大的值，是不是小于等于d，如果是，则有可能存在鬼。

详见代码：

#include<bits/stdc++.h>
#define maxn 100005
using namespace std;

int n,m,d;
int dist[3][maxn];
int mark[maxn];
vector<int> graph[maxn];
queue<int> que;

int bfs(int num,int s){
    while(que.size()) que.pop();
    dist[num][s] = 0;
    que.push(s);
    int ret = -1;
    while(que.size()){
        int temp = que.front();
        que.pop();
        for(int i = 0;i < graph[temp].size();++i){
            int to = graph[temp][i];
            if(dist[num][to] != -1) continue;
            dist[num][to] = dist[num][temp] + 1;
            if(mark[to]){
                if(ret == -1 || dist[num][ret] < dist[num][to]){
                    ret = to;
                }
            }
            que.push(to);
        }
    }
    return ret;
}

int main(){
    scanf("%d%d%d",&n,&m,&d);
    for(int i = 0;i < m;++i){
        int p;
        scanf("%d",&p);
        mark[p] = 1;
    }
    int u,v;
    for(int i = 0;i < n - 1;++i){
        scanf("%d%d",&u,&v);
        graph[u].push_back(v);
        graph[v].push_back(u);
    }
    memset(dist,-1,sizeof(dist));
    int v1 = bfs(0,1);
    int v2 = bfs(1,v1);
    bfs(2,v2);
    int cnt = 0;
    for(int i = 1;i <= n;++i){
        int d1 = dist[1][i],d2 = dist[2][i];
        if(max(d1,d2) <= d) ++cnt;
    }
    printf("%d\n",cnt);
    return 0;
}

 

转载于:https://www.cnblogs.com/tiberius/p/9165788.html