cf 405E Graph Cutting(dfs)

传送门：https://codeforces.com/problemset/problem/405/E
题目大意：给一个无向图，没有重边，自环，问能否切割成由3个点，2条边组成的图，每条边只能用一次，每个点可用多次。
思路：dfs。把环展开，把图变成树，操作如图。

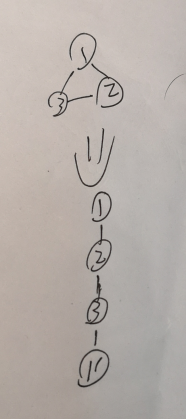
dfs完自动形成的一棵dfs树。

对一棵树来说，如果只有奇数条边，肯定NO solution，偶数有解，原因如下：
从下网上删边，如果有偶数个叶节点，两两配对删掉就行了；奇数的话，删到剩下一个，跟他的父节点组成一个图。由于总共有偶数条边，每次删两条，删到最后就剩两条边，就是以下两种情况：

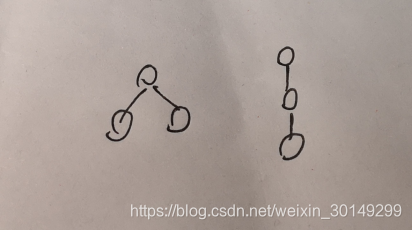
都满足题意。

代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll M=1e5+10;
ll n,m;
struct Edge{
	ll u,v;
	Edge(){}
	Edge(ll u,ll v){this->u=u,this->v=v;}
}e[M];
vector<ll> G[M];
bool vis[M],used[M];
void dfs(ll x,ll pa){//x是当前节点，x从pa边过来
	vis[x]=1;//一个点搜一次
	vector<ll> son;//与子节点相连的边
	for(ll i=0;i<G[x].size();i++){
		ll t=G[x][i];
		if(e[t].u==x && !vis[e[t].v])
			dfs(e[t].v,t);
		else if(!vis[e[t].u])
			dfs(e[t].u,t);
	}
	for(ll i=0;i<G[x].size();i++)
		if(!used[G[x][i]] && G[x][i]!=pa){
			son.push_back(G[x][i]);//记录未使用过的，跟子节点相连的边
		}
	ll cnt=son.size();
	if(cnt&1){//奇数条边时，特殊处理
		ll t=son[cnt-1];cnt--;
		used[pa]=used[t]=1;//标记边已经使用过了
		printf("%lld %lld %lld\n",(e[pa].u==x)?(e[pa].v):(e[pa].u),x,(e[t].u==x)?(e[t].v):(e[t].u));
	}
	for(ll i=0;i<cnt/2;i++){
		ll t1=son[i],t2=son[cnt-1-i];
		used[t1]=used[t2]=1;
		printf("%lld %lld %lld\n",(e[t1].u==x)?(e[t1].v):(e[t1].u),x,(e[t2].u==x)?(e[t2].v):(e[t2].u));
	}
}

int main(){
	scanf("%lld%lld",&n,&m);
	ll t=0;
	for(ll i=0;i<m;i++){
		ll u,v;
		scanf("%lld%lld",&u,&v);
		G[u].push_back(t),G[v].push_back(t);
		e[t++]=Edge(u,v);
	}
	if(m&1) return printf("No solution\n")*0;
	dfs(1,-1);
	return 0;
}