简介:概率论是数学的一个分支,关注随机现象的规律,对统计学、信息论、机器学习等领域至关重要。此习题集提供了一系列概率论练习题目和详尽解答,包含概率论的基本概念如事件、样本空间、概率,以及条件概率、独立事件、伯努利试验、二项分布、离散和连续随机变量、大数定律、中心极限定理、概率分布(包括均匀分布、正态分布、泊松分布)、期望值、方差等主题。高级主题可能包括随机过程和马尔科夫链。这套习题集旨在帮助学习者深刻理解概率论,并提升实际问题分析和解决的技能。 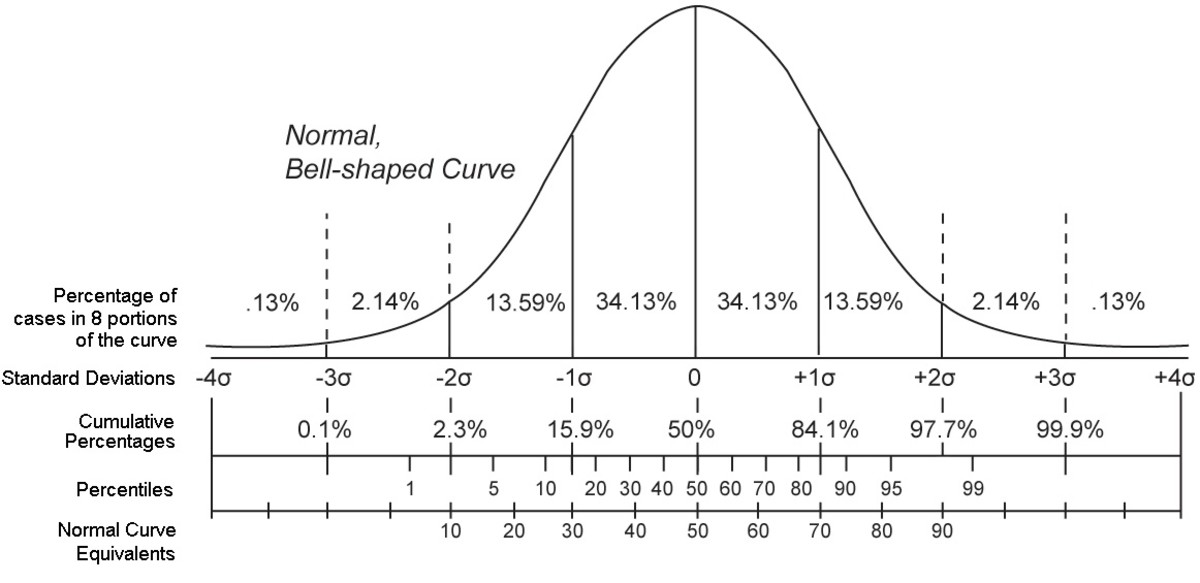
1. 概率论基本概念的探索
概率论是数学的一个分支,它研究随机事件及其发生的可能性。在这一章节中,我们将探索概率论的一些基础概念,为理解后续章节的高级主题打下坚实的基础。
1.1 随机实验与基本事件
随机实验是概率论的核心概念之一,它指的是在一定条件下,其结果具有不确定性的实验。例如,抛硬币、掷骰子等都属于典型的随机实验。每一个可能的结果被称为一个基本事件。基本事件构成的集合称为样本空间,表示为 Ω,它是概率论中最为基本的概念之一。
1.2 概率的定义与性质
概率是衡量一个事件发生可能性的数学度量,通常定义为该事件发生的基本事件数与样本空间中基本事件总数的比值。概率具有非负性、规范性和可加性等基本性质。理解和掌握这些性质对于后续进行更复杂的概率计算至关重要。
1.3 组合数学与概率计算
在计算复杂事件的概率时,经常需要使用组合数学中的计数原理。通过组合计数方法,我们可以确定在多种可能情况中,特定事件发生的概率。例如,组合数、排列数等概念在计算离散随机变量的概率时显得尤为重要。
通过本章的学习,读者将对概率论有初步的了解,并为其在更高级主题中的应用打下基础。接下来的章节,我们将深入探讨条件概率、独立事件以及伯努利试验等,逐步揭开概率论的奥秘。
2. 深入理解条件概率与独立事件
2.1 条件概率的数学定义与性质
2.1.1 条件概率的基本公式
条件概率描述的是在某个条件或事件已经发生的情况下的概率,表示为P(A|B),其中A是目标事件,B是条件事件。根据概率论中的定义,条件概率可以由以下公式计算得出:
[ P(A|B) = \frac{P(A \cap B)}{P(B)} ]
在上述公式中,(P(A \cap B)) 表示事件A和事件B同时发生的概率,而(P(B))是事件B发生的概率。只有当(P(B) \neq 0)时,条件概率才有意义。
为了更深刻理解这一概念,我们可以考虑一个简单的例子。假设我们有两个盒子,一个包含2个红球和3个蓝球,另一个包含1个红球和4个蓝球。我们随机选择一个盒子然后从中抽取一个球,我们想要计算的是在已知抽取的球是红球的情况下,该球来自第一个盒子的概率。
2.1.2 条件概率的计算技巧
计算条件概率时,理解并应用乘法规则和加法规则是十分关键的。乘法规则描述了两个事件同时发生的概率,表示为:
[ P(A \cap B) = P(A|B) \times P(B) ]
此规则是直接从条件概率的定义中推导出来的。
加法规则则描述了两个互斥事件至少有一个发生的概率,表示为:
[ P(A \cup B) = P(A) + P(B) - P(A \cap B) ]
如果事件A和事件B不是互斥的,还需要从上述结果中减去它们同时发生的概率。
2.1.3 条件概率在现实问题中的应用
条件概率在许多领域都有广泛的应用,从简单的决策分析到复杂的统计推断中都有所体现。例如,在机器学习中的朴素贝叶斯分类器,就是基于条件概率来预测未知类别的概率。在医疗诊断中,医生可能会利用条件概率来评估某些症状出现时患有某种疾病的概率。
2.2 独立事件的界定及实例分析
2.2.1 独立事件的定义及其判断方法
两个事件A和B是独立的,当且仅当一个事件的发生不影响另一个事件发生的概率。这意味着:
[ P(A \cap B) = P(A) \times P(B) ]
如果两个事件满足上面的关系,那么就可以认为这两个事件是独立的。
在实际应用中,判断事件的独立性通常需要对事件本身有深入的理解。例如,在抛硬币的实验中,每次抛掷的结果被认为是独立的,因为前一次抛掷的结果不会影响下一次的结果。
2.2.2 独立事件的概率计算
当两个事件是独立事件时,我们可以用乘法来计算它们同时发生的概率。根据独立事件的定义,可以推出:
[ P(A \cap B) = P(A) \times P(B) ]
这意味着,如果我们知道A和B各自的概率,就可以直接通过乘法来得到它们同时发生的概率。
举个例子,考虑两个简单的事件:掷骰子得到一个“6”和抛硬币得到“正面”。假设骰子是公正的,硬币也是均匀的,那么这两个事件是独立的。因此,掷得“6”和抛得“正面”同时发生的概率就是1/6乘以1/2,等于1/12。
2.2.3 独立事件的逻辑与直觉辨析
在直观上,独立事件的含义可能并不是立即显而易见的。直觉上,我们可能会认为两个事件之间存在某种联系,而事实上,它们是独立的。例如,在评估统计数据时,人们可能会错误地假设两个相关事件是因果关系,而实际上它们可能是独立的,或者存在隐藏的变量影响两者。
独立性也与条件概率形成鲜明对比。如果两个事件是独立的,条件概率公式中的(P(A|B))将会简化为(P(A))。这个特性是我们在进行概率计算时的关键区分点。
理解独立事件,不仅可以帮助我们正确地计算概率,还能让我们在分析复杂情况时避免错误的因果推断,从而更加客观地分析数据,做出正确的决策。
3. 伯努利试验与二项分布的实践探究
3.1 伯努利试验的概念及特征
3.1.1 伯努利试验的定义与应用领域
伯努利试验是概率论中的一个基本概念,指的是在相同的条件下重复进行的一次实验,其结果只有两种可能:成功(记作1)或失败(记作0)。这种试验在统计学、数据分析、质量控制和许多自然科学与社会科学的领域中有着广泛的应用。例如,在投掷硬币的实验中,正面朝上可以视为“成功”,反面朝上则视为“失败”。
3.1.2 伯努利试验的统计性质与计算方法
伯努利试验的统计性质是基于大量重复试验的基础上得出的。统计学中,伯努利试验的核心性质是其结果的二项分布特性。当我们关心在n次独立重复的伯努利试验中,成功k次的概率时,就可以用二项分布来描述。
3.1.3 伯努利试验的实际应用案例
举个实际应用的例子,比如在一个生产线上,检验产品是否合格。假定每个产品合格的概率是p,不合格的概率则是1-p。如果进行n次这样的检验,我们可以使用二项分布来计算恰好有k个合格品的概率。
3.2 二项分布的深入解析与计算
3.2.1 二项分布的概率质量函数
二项分布描述了在固定次数n的独立伯努利试验中,成功的次数k的概率分布。其概率质量函数(PMF)可以表示为:
P(X=k) = C(n,k) * p^k * (1-p)^(n-k)
其中, C(n,k) 是组合数,表示从n次试验中选择k次成功的组合方式数目, p 是每次试验成功的概率。
3.2.2 二项分布的期望值和方差
二项分布的期望值(平均值)和方差是其两个重要的特征量,分别代表了分布的中心位置和分布的离散程度。它们分别用以下公式计算:
- 期望值:
E(X) = n * p - 方差:
Var(X) = n * p * (1 - p)
3.2.3 二项分布在现实中的应用实例
在现实生活中,二项分布的应用非常广泛。一个典型的例子是在市场调查中,估计产品满意度。假设某公司推出一款新产品,想估计大约有多少比例的消费者会满意。通过随机抽取一定数量的消费者并询问他们是否满意,可以使用二项分布来估计不同满意度比例的概率。
下面是用Python代码来计算二项分布的例子:
from scipy.stats import binom
# 设定试验次数和成功概率
n, p = 10, 0.5
# 创建一个二项分布的离散随机变量实例
rv = binom(n, p)
# 计算在10次试验中恰好得到5次成功的概率
prob_5_success = rv.pmf(5)
print(f"恰好得到5次成功的概率为: {prob_5_success:.4f}")
# 期望值和方差
expectation = rv.mean()
variance = rv.var()
print(f"期望值为: {expectation}, 方差为: {variance}")
以上代码展示了如何使用 scipy.stats 库来创建一个二项分布的随机变量,并计算特定成功次数的概率,以及如何获取其期望值和方差。
接下来,我们会探索如何在不同的场合应用二项分布,并用实际的数据来进行模拟和预测。
4. 随机变量与概率分布的综合应用
4.1 离散随机变量与连续随机变量的对比
4.1.1 离散随机变量的特征描述
在概率论与统计学中,随机变量是用于描述随机现象的重要工具。它将随机事件的结果与实数对应起来,可以是离散的,也可以是连续的。离散随机变量拥有可数的取值范围,例如投掷骰子出现的点数、成功或失败的结果等。与连续随机变量相比,离散随机变量的研究和应用有着不同的统计特性与方法。
在研究离散随机变量时,需要关注其概率质量函数(probability mass function, PMF),PMF 描述了随机变量取每个具体值的概率。通过PMF,我们可以了解随机变量取某一特定值的概率大小,进而推断整个随机过程的概率特性。
例如,考虑一个简单的离散随机变量X,它表示抛一枚公平硬币的次数直到出现正面为止。这个随机变量可能取值为1, 2, 3, ...。其概率质量函数可以表示为:
- P(X=1) = 0.5
- P(X=2) = 0.25
- P(X=3) = 0.125
- ...
4.1.2 连续随机变量的概率密度函数
与离散随机变量不同,连续随机变量拥有不可数的取值范围,例如人的身高、降雨量等。这种类型的随机变量通过概率密度函数(probability density function, PDF)来描述。虽然连续随机变量在任意一个具体的点上的概率为零,但通过概率密度函数可以在某个区间上计算随机变量取值的概率。
概率密度函数具有以下性质: - f(x) ≥ 0,其中 f(x) 是概率密度函数。 - ∫f(x)dx = 1,即概率密度函数曲线下的总面积为1,代表所有可能事件的全部概率。
以标准正态分布为例,其概率密度函数表达式为:
f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
4.1.3 不同类型随机变量的选择与应用
在实际应用中,选择哪一种类型的随机变量取决于实际问题和数据特性。通常,如果一个随机事件的结果是有限个或可数无限个,选择离散随机变量会更加方便;反之,如果结果是连续的或者取值范围极其广阔,连续随机变量则更为合适。
在选择合适类型的随机变量后,我们可以进一步应用各种概率分布进行数据分析、决策制定和风险评估。下面列举一些常见的离散和连续概率分布的例子,并将在后续小节中详细解析。
4.2 常见概率分布类型的详细解读
4.2.1 均匀分布、正态分布、泊松分布的特点
均匀分布、正态分布和泊松分布是概率论中三种非常重要的连续概率分布。
均匀分布
均匀分布是一种最简单的连续概率分布,其特点是所有取值区间的概率相等。例如,一个理想的骰子每个面朝上的概率都是1/6。数学上,均匀分布可以表示为:
f(x) = \frac{1}{b - a} \text{ for } a \leq x \leq b
正态分布
正态分布(又称高斯分布)广泛用于自然界和社会科学中,其形状呈钟形曲线,是对称的。它的两个参数为均值(μ)和标准差(σ)。正态分布的表达式为:
f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
泊松分布
泊松分布是描述在固定时间间隔或空间区域内发生的随机事件的次数的概率分布。它常用于描述稀有事件的发生频率。泊松分布的概率质量函数为:
f(k; \lambda) = \frac{e^{-\lambda}\lambda^k}{k!}
其中,λ是单位时间(或单位空间)内事件发生的平均次数。
4.2.2 各分布类型的适用场景与实际例子
每种概率分布都有其适用的场景和领域。例如:
- 均匀分布 常用于模拟随机选取、投骰子等游戏场景;
- 正态分布 在自然和社会科学中无处不在,例如人的身高、考试成绩分布等;
- 泊松分布 适用于描述交通事故、呼叫中心的电话呼叫次数等情况。
在实际应用中,我们如何选择合适的概率分布?通常,我们需要对数据进行充分的了解,通过可视化工具(如直方图)来观察数据的分布情况,然后选择一个与数据特性最匹配的概率分布。
4.2.3 分布参数的估计方法
对于概率分布,我们通常需要估计其参数,即确定分布的具体形态。参数估计的方法主要有两种:点估计和区间估计。
点估计 是使用样本数据来确定总体参数的一个具体值,常用的方法有矩估计法和最大似然估计法。举个例子,如果我们想要估计一个正态分布的均值μ,我们可以用样本均值作为μ的一个估计。
\hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i
其中,xi 是样本数据,n 是样本大小。
区间估计 提供一个参数的估计区间,这个区间有一定的置信水平表示参数落入该区间的概率。例如,对于正态分布的均值μ的95%置信区间,我们可以使用以下公式:
\bar{x} \pm 1.96 \times \frac{\sigma}{\sqrt{n}}
这里,1.96 是对应于正态分布的95%置信水平的Z-分数。
总的来说,概率分布的选择与应用是统计推断和数据分析中的核心内容。通过对随机变量的理解和概率分布的应用,研究者能够更好地描述和预测现实世界中的随机现象。在下一章节,我们将探索这些概率分布如何应用于具体的统计模型和决策过程中。
5. 概率论的高级主题与定理解析
5.1 大数定律与中心极限定理的理论内涵
大数定律和中心极限定理是概率论中非常重要的两个定理,它们在统计学、数据分析以及金融领域中有着广泛的应用。我们首先来探讨大数定律。
5.1.1 大数定律的数学表述及其意义
大数定律描述了当试验次数足够多时,样本均值会以概率收敛到期望值这一现象。其数学表述如下:
设有相同的独立随机变量序列 ({X_1, X_2, ..., X_n}),每个随机变量 (X_i) 都有相同的期望 (E(X_i) = \mu) 和方差 (Var(X_i) = \sigma^2),则对于任意的正数 (\epsilon),当 (n) 趋向于无穷大时,有:
[ P\left(\left|\frac{1}{n}\sum_{i=1}^{n}X_i - \mu\right| < \epsilon\right) \rightarrow 1 ]
这个定理的意义在于,它为大样本推断提供了理论基础。例如,在统计抽样中,样本均值能很好地估计总体均值,这是抽样调查与估计的基石。
5.1.2 中心极限定理的证明与应用
中心极限定理告诉我们,大量的独立同分布的随机变量之和,当随机变量数量足够多时,其分布接近正态分布,无论原分布是什么。其数学表述为:
设有独立同分布的随机变量序列 ({X_1, X_2, ..., X_n}),其期望为 (\mu),方差为 (\sigma^2),则对于足够大的 (n),随机变量之和:
[ Z_n = \frac{\sum_{i=1}^{n}X_i - n\mu}{\sigma\sqrt{n}} ]
将趋近于标准正态分布 (N(0,1))。
这个定理在实际应用中非常广泛,例如在质量控制、金融建模等领域,即使我们不知道单个数据的具体分布,但通过中心极限定理,我们可以使用正态分布进行近似计算。
5.1.3 大数定律与中心极限定理在统计中的作用
这两个定理在统计学中的作用是基础性的。它们为从样本数据估计总体参数提供了数学保障,使得我们能够进行有效的统计推断。例如,在对某一产品的质量进行抽样检验时,如果样本量足够大,样本均值将非常接近总体均值,从而可以作为总体均值的一个很好的估计。中心极限定理进一步保证了误差项的分布接近正态,为统计检验和区间估计提供了条件。
5.2 随机过程与马尔科夫链的探索
随机过程与马尔科夫链在模拟复杂系统动态行为方面具有独特的价值,应用范围非常广泛,包括金融、生物学、通信网络、人工智能等。
5.2.1 随机过程的基本概念与分类
随机过程是随机变量的一组集合,这些变量是按时间或其他变量的顺序排列的。简单地说,随机过程是随时间发展的随机现象的数学模型。
随机过程可以分为几个主要类别:
- 离散时间与连续时间
- 离散状态与连续状态
- 马尔科夫过程和非马尔科夫过程
其中,马尔科夫过程中的马尔科夫链是研究最为深入的一种类型,因为它的状态转移只与当前状态有关,而与历史状态无关,即具有无记忆性。
5.2.2 马尔科夫链的定义、性质及转移矩阵
马尔科夫链是一类特殊的随机过程,其每一步的状态转移仅依赖于前一步的状态。其定义可以通过转移矩阵清晰表示。设 (X_n) 为马尔科夫链在时间 (n) 的状态,则转移概率定义为:
[ P_{ij} = P(X_{n+1} = j | X_n = i) ]
这里的转移矩阵 (P) 是一个方阵,其中元素 (P_{ij}) 表示从状态 (i) 转移到状态 (j) 的概率。
马尔科夫链的一个重要性质是状态分类,其中包括:
- 吸收状态:一旦进入,系统就不会离开。
- 非吸收状态:系统可以从该状态转移到其他状态。
5.2.3 马尔科夫链在模拟与预测中的应用实例
在实际应用中,马尔科夫链可以用来模拟用户行为、股票价格变动、自然语言处理等。例如,在金融市场分析中,马尔科夫链可以模拟资产价格的状态转移,为投资决策提供依据。在自然语言处理中,通过构建文本中词汇或词组的马尔科夫链模型,可以进行文本生成和语义分析。此外,马尔科夫链也可以用于预测网页访问模式、搜索路径等互联网相关问题。
通过以上章节的深入学习,我们可以看到概率论中的高级主题和定理不仅仅是理论上的抽象概念,它们在解决现实世界问题中扮演着不可或缺的角色。
简介:概率论是数学的一个分支,关注随机现象的规律,对统计学、信息论、机器学习等领域至关重要。此习题集提供了一系列概率论练习题目和详尽解答,包含概率论的基本概念如事件、样本空间、概率,以及条件概率、独立事件、伯努利试验、二项分布、离散和连续随机变量、大数定律、中心极限定理、概率分布(包括均匀分布、正态分布、泊松分布)、期望值、方差等主题。高级主题可能包括随机过程和马尔科夫链。这套习题集旨在帮助学习者深刻理解概率论,并提升实际问题分析和解决的技能。
























 328
328

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








