本文探讨了量子力学中的希尔伯特空间概念，解释了平方可积函数如何构成L2空间，并讨论了内积的重要性。希尔伯特空间内的函数通过正交归一化基的线性组合表示，这与线性代数的向量空间有相似的运算规则，显示了线性代数在量子力学中的核心地位。
希望能够通过分享自己学习笔记和心得的方式来加深对所学内容的理解，欢迎批评指正。
使用教材：David J. Griffiths 《Introduction to Quantum Mechanics》
3.1 希尔伯特空间
1. 如何理解希尔伯特空间
我们知道，描述一个可能的物理态的波函数都需要满足归一化条件：
这意味着，所有波函数在特定区间(a, b)（通常是（-无穷, +无穷））都是方平可积，即：
这样的函数有什么特点呢？会发现假设f (x )和g (x ) 是平方可积的，则：
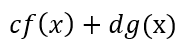
也是平方可积的，其中c 和d 均为常数。我们知道在线性代数中，满足这样关系的所有向量可以构成一个向量空间。那么根据线性代数的概念，我们可以定义一个由所有平方可积函数组成的空间，在数学上这个空间称
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
