本文是OpenGL 4.0 Shading Language Cookbook的学习笔记。
通常我们通过在模型边缘和褶皱处绘制轮廓线来实现卡通或手绘效果。在本文,我们将讨论如何使用几何着色器来产生额外的轮廓线。这里,我们使用四边形来近似轮廓线。
下图显示了使用几何着色器生成的黑色轮廓线。这些轮廓线由较小的四边形产生。
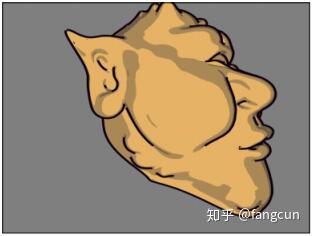
本文介绍的这一技术来自Philip Rideout的博客(prideout.net/blog/?p=54)。他的实现使用了两遍处理,并且包含了很多优化,比如反走样和自定义深度测试(通过g-buffers)。我们的目的是为了演示几何着色器的特性,为了保持简单易懂,我们的实现只进行了一遍处理,且没有进行反走样和自定义深度测试。如果你对这些附加处理很感兴趣,可以阅读Philip的博客。
几何着色器可以为输入的图元附加其它信息,同时还可以访问图元的邻接顶点信息。下面是访问邻接顶点的一些常量定义:
- GL_LINES_ADJACENCY:线段以及相邻顶点(4个顶点)。
- GL_LINE_STRIP_ADJACENCY:连线以及相邻顶点(对于n条线,有n+3个顶点)。
- GL_TRIANGLES_ADJACENCY:三角形以及相邻三角形(每个图元有6个顶点)。
- GL_TRIANGLES_STRIP_ADJACENCY:三角形带以及相邻三角形(对于n个三角形,有2(n+2)个顶点)。
对于每个常量的详细说明,可以参考OpenGL官方文档。在本文,我们GL_TRIANGLES_ADJACENCY模式提供网格中的邻接三角形的信息。在这个模式下,每个图元包含6个顶点。下图显示了这些顶点的位置:
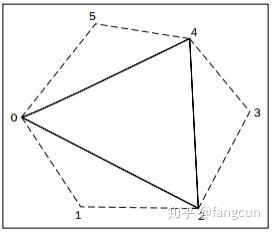
图中实线表示三角形本身,虚线表示邻接三角形。第1个,第3个和第5个顶点组成了三角形本身。第2个,第4个和第6个组成了邻接三角形。
网格数据通常不是以这种形式组织,所以,我们需要对我们的网格进行预处理使它变成上面的形式。通常,这意味着我们需要把索引数组扩展为原来的两倍。位置,法线和纹理坐标数组保持不变。
我们通过邻接三角形来判定一条边是否使褶皱的一部分。我们假定一条边是褶皱,如果这个三角形是正面的,但对应的邻接三角形不是正面。
我们通过计算三角形的法线(使用叉积运算)判断一个三角形是正面还是反面。在剪切空间下,法线的z坐标如果为正那么三角形为正面。所以,我们只需要计算法线的z坐标就可以。对于一个顶点为A,B,C的三角形,法线的z坐标可以用下面的式子计算:
确定一条边为褶皱后,几何着色器会产生一个四边形来覆盖这条褶皱边。这些四边形放在一起,就组成上图中的褶皱部分。生成完所有的四边形后,几何着色器会输出原始的三角形。
为了在一遍处理中绘制网格和轮廓线,我们添加了一个输出变量,用于在片段着色器中判断图元是网格还是我们生成的四边形,然后使用对应的着色方法进行着色。
实现
之前提到,我们需要扩展索引数组来存放附加的邻接三角形信息。我们可以通过查找网格中的公共边来完成扩展。由于篇幅限制,这里就不详细讨论具体实现,前面提到的博客有如何实现它的具体说明。本文的代码中包含了一个简单的方法来实现它(但不够高效)。
本例还使用了下面这些Uniform变量:
- EdgeWidth:剪切空间(规范空间)下的轮廓线宽度。
- PctExtend:覆盖褶皱边的四边形扩展的百分比。
- LineColor:轮廓线颜色。
还有一些用于模型着色和矩阵变换的Uniform变量需要我们设置。
我们采取以下步骤来渲染模型轮廓线:
1. 使用下面的代码作为顶点着色器:
#version 400
layout (location = 0 ) in vec3 VertexPosition;
layout (location = 1 ) in vec3 VertexNormal;
out vec3 VNormal;
out vec3 VPosition;
uniform mat4 ModelViewMatrix;
uniform mat3 NormalMatrix;
uniform mat4 ProjectionMatrix;
uniform mat4 MVP;
void main()
{
VNormal = normalize( NormalMatrix *
VertexNormal);
VPosition = vec3(ModelViewMatrix *
vec4(VertexPosition,1.0));
gl_Position = MVP * vec4(VertexPosition,1.0);
}2. 使用下面的代码作为几何着色器:
#version 400
layout( triangles_adjacency ) in;
layout( triangle_strip, max_vertices = 15 ) out;
out vec3 GNormal;
out vec3 GPosition;
// Which output primitives are silhouette edges
flat out bool GIsEdge;
in vec3 VNormal[]; // Normal in camera coords.
in vec3 VPosition[]; // Position in camera coords.
uniform float EdgeWidth;
// Width of sil. edge in clip cds.
uniform float PctExtend; // Percentage to extend quad
bool isFrontFacing( vec3 a, vec3 b, vec3 c )
{
return ((a.x * b.y - b.x * a.y) +
(b.x * c.y - c.x * b.y)
+ (c.x * a.y - a.x * c.y)) > 0;
}
void emitEdgeQuad( vec3 e0, vec3 e1 )
{
vec2 ext = PctExtend * (e1.xy - e0.xy);
vec2 v = normalize(e1.xy – e0.xy);
vec2 n = vec2(-v.y, v.x) * EdgeWidth;
// Emit the quad
GIsEdge = true;//This is part of the sil. edge
gl_Position = vec4( e0.xy - ext, e0.z, 1.0 );
EmitVertex();
gl_Position =vec4(e0.xy- n - ext,e0.z,1.0);
EmitVertex();
gl_Position = vec4( e1.xy + ext, e1.z, 1.0 );
EmitVertex();
gl_Position = vec4( e1.xy - n + ext, e1.z,
1.0 );
EmitVertex();
EndPrimitive();
}
void main()
{
vec3 p0 = gl_in[0].gl_Position.xyz /
gl_in[0].gl_Position.w;
vec3 p1 = gl_in[1].gl_Position.xyz /
gl_in[1].gl_Position.w;
vec3 p2 = gl_in[2].gl_Position.xyz /
gl_in[2].gl_Position.w;
vec3 p3 = gl_in[3].gl_Position.xyz /
gl_in[3].gl_Position.w;
vec3 p4 = gl_in[4].gl_Position.xyz /
gl_in[4].gl_Position.w;
vec3 p5 = gl_in[5].gl_Position.xyz /
gl_in[5].gl_Position.w;
if( isFrontFacing(p0, p2, p4) ) {
if( ! isFrontFacing(p0,p1,p2) )
emitEdgeQuad(p0,p2);
if( ! isFrontFacing(p2,p3,p4) )
emitEdgeQuad(p2,p4);
if( ! isFrontFacing(p4,p5,p0) )
emitEdgeQuad(p4,p0);
}
// Output the original triangle
GIsEdge = false;
// This triangle is not part of an edge.
GNormal = VNormal[0];
GPosition = VPosition[0];
gl_Position = gl_in[0].gl_Position;
EmitVertex();
GNormal = VNormal[2];
GPosition = VPosition[2];
gl_Position = gl_in[2].gl_Position;
EmitVertex();
GNormal = VNormal[4];
GPosition = VPosition[4];
gl_Position = gl_in[4].gl_Position;
EmitVertex();
EndPrimitive();
}3. 使用下面的代码作为片段着色器:
#version 400
//*** Light and material uniforms go here ****
uniform vec4 LineColor; // The sil. edge color
in vec3 GPosition; // Position in camera coords
in vec3 GNormal; // Normal in camera coords.
flat in bool GIsEdge;
// Whether or not we're drawing an edge
layout( location = 0 ) out vec4 FragColor;
vec3 toonShade( )
{
// *** 之前专栏文章中的卡通着色代码 ***
}
void main()
{
//If we're drawing an edge,use constant color,
//otherwise,shade the poly.
if( GIsEdge ) {
FragColor = LineColor;
} else {
FragColor = vec4( toonShade(), 1.0 );
}
}原理
在顶点着色器中,我们将顶点位置,法线转换到相机坐标系,并通过变量VPosition和VNormal将它们传递到下一阶段。同时变量gl_Position被设置为经过模型视图投影变换后的坐标。
我们使用下面的代码定义几何着色器的输入和输出。
layout( triangles_adjacency ) in;
layout( triangle_strip, max_vertices = 15 ) out;上面代码表示输入图元类型是带有邻接信息的三角形,输出图元类型为三角形带。几何着色器会产生一个三角形(和输入的三角形一模一样),以及最多一个四边形用来覆盖褶皱,最多输出15个顶点。
输出变量GIsEdge用于在片段着色器表明片段是否是褶皱四边形的一部分,从而选择使用对应的着色方法。它只是一个布尔量,我们不需要对它进行插值,所以对它使用flat限定符。
在main函数中,我们对所有6个顶点的坐标除以它们的w成分来将坐标转换到笛卡尔坐标系。这一步对于透视投影是必须的,但对于平行投影是不必的。
接着,我们需要确定主三角形(由顶点0,2,4构成的三角形)是否是正面的。函数isFrontFacing使用我们前面提到的式子计算三角形是否为正面。如果三角形是正面的,对于它的边,如果对应的三角形不是正面的,我们就生成一条四边形覆盖褶皱。
函数emitEdgeQuad用于产生和边对齐的四边形。这条边由它的参数e0和e1定义。从e0出发到e1构成向量ext,然后我们将向量ext乘以PctExtend进行缩放。对其进行缩放是为了通过延长四边形来遮盖两个四边形之间的空隙(我们将在优化小节对这一问题进行讨论)。
我们在这里忽略了z坐标。我们的点都定义在剪切空间,并且我们生成的四边形都和x-y平面对齐(面对相机)。我们直接使用了每个顶点最后的位置坐标,不做任何变换。
接着,变量v被赋值为从e0到e1的单位向量。变量n赋值为与v正交的向量(在二维空间,我们可以通过交换x,y坐标,并将交换后的x坐标取相反数得到一个向量的正交向量),也就v向量逆时针旋转90度。我们将n向量以EdgeWidth为系数进行缩放,来使向量n的长度和四边形宽度一样。向量ext和向量n结合得到四边形,如下图所示:
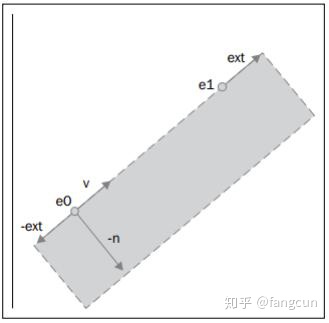
四边形的四个角分别是:e0-ext,e0-n-ext,e1+ext和e1-n+ext。较低的两个顶点的z坐标和e0的z坐标相同,较高的两个顶点和z坐标和e1的z坐标相同。
在emitEdgeQuad函数,我们设置变量GIsEdge来使片段着色器对褶皱采用不同的着色方法。我们还输出了四边形的四个顶点,最后我们调用EndPrimitive函数结束图元定义。
回到main函数,生成褶皱边后,我们输出不做任何改变输出原始的三角形。顶点0,2和4的VNormal,VPosition和gl_Position不做修改传递给片段着色器。
在片段着色器,我们根据变量GIsEdge的值选择着色方法。
优化
前面提到,这一技术存在一个问题:两个褶皱四边形之间可能出现缝隙。

我们可以看到上图的褶皱之间存在缝隙。我们可以用三角形来填充这个缝隙,这里我们通过延长四边形来简化处理,但这样做,可能会造成一定的人工痕迹,但在实践中,这种处理看起来还不错。
另一个问题和深度测试相关。如果一条褶皱扩展长度到网格的另一区域,褶皱就可能因为深度测试而被剪切掉。下图就是一个例子:

褶皱垂直穿过了图像的中间部分,但由于褶皱处于网格之后,部分被剪切掉。这个问题可以通过在渲染褶皱时使用自定义深度测试来解决。具体细节参考之前提到的博客。也可以在绘制褶皱时关闭深度测试,还需要注意不要再模型背面绘制褶皱。




















 35
35

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








