findwindowex子窗口类型有哪几种_「leetcode」209.长度最小的子数组：滑动窗口拯救了你...

最新推荐文章于 2023-02-01 19:58:18 发布

原创最新推荐文章于 2023-02-01 19:58:18 发布 · 275 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#findwindowex子窗口类型有哪几种

本文介绍了如何使用滑动窗口算法优化求解数组中最短连续子数组使得其和大于等于给定值s的问题。从暴力解法的O(n^2)到滑动窗口算法的O(n)，详细解析了滑动窗口的原理和实现，通过示例和动画展示了滑动窗口如何动态调整子数组起点，降低了时间复杂度。最后给出了C++的滑动窗口代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

别不信，真的拯救了你

题目209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：
输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

暴力解法

这道题目暴力解法当然是两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2) 。

代码如下：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：O(n^2)
空间复杂度：O(1)

滑动窗口

接下来就开始介绍数组操作中另一个重要的方法：「滑动窗口」。

所谓滑动窗口，「就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果」。

这里还是以题目中的示例来举例，s=7，数组是 2，3，1，2，4，3，来看一下查找的过程：

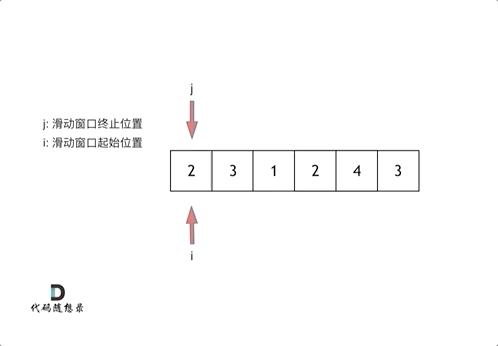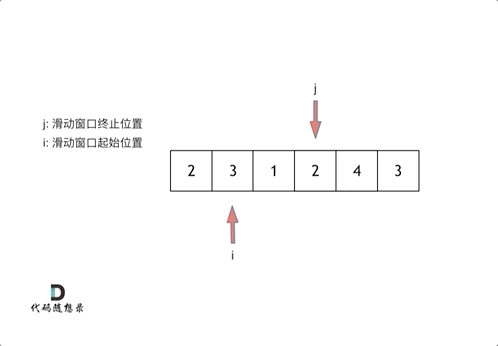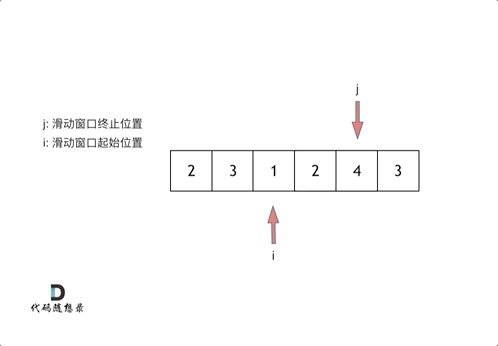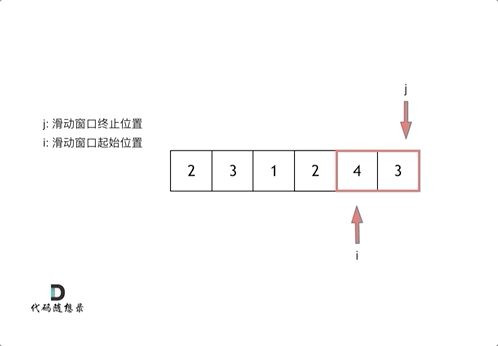
最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？

窗口就是满足其和 ≥ s 的长度最小的连续子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，窗口的起始位置设置为数组的起始位置就可以了。

解题的关键在于窗口的起始位置如何移动，如图所示：

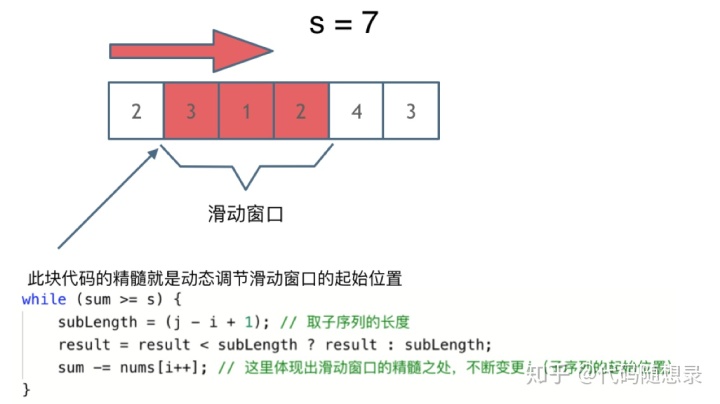
可以发现「滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。」

C++滑动窗口代码

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

本文：

https://github.com/youngyangyang04/leetcode-mastergithub.com

已经收录，里面还有leetcode刷题攻略、各个类型经典题目刷题顺序、思维导图，可以fork到自己仓库，有空看一看一定会有所收获，如果对你有帮助也给一个star支持一下吧！ 我的B站（里面有我讲解的算法视频已经编程相关知识）：

哔哩哔哩 ( ゜- ゜)つロ乾杯~ Bilibilispace.bilibili.com

我是程序员Carl，哈工大师兄，先后在腾讯和百度从事技术研发多年，利用工作之余重刷leetcode，更多精彩算法文章尽在：代码随想录，关注后，回复「Java」「C++」「python」「简历模板」等等，有我整理多年的学习资料，可以加我微信，备注「个人简介」+「组队刷题」，拉你进入刷题群（无任何广告，纯个人分享），每天一道经典题目分析，我选的每一道题目都不是孤立的，而是由浅入深一脉相承的，如果跟住节奏每篇连续着看，定会融会贯通。