java实现曲线运动_分层动画实现元素的曲线运动

在前端实现元素的动画需要用到transition或者animation搭配transform做位移的效果，但这只能实现元素沿着直线运动。如果想要让元素沿着曲线运动，则需要用到本文介绍的“分层动画”。

分层动画

大家还记得高中物理的“平抛运动”吗？运动轨迹为一条曲线，它可以看成是水平方向上的匀速运动和垂直方向上的自由落体的组合。更进一步，运动轨迹为曲线必须在水平与垂直两个方向上有不同的以时间为自变量的路径函数f(t)。

以此类推到前端，过渡与动画中的属性time-function就是以时间为自变量的路径函数f(t)，只要让元素在水平和垂直方向上有不同的time-function，就可实现曲线运动的效果。接着我们将使用分层动画法，让元素同时沿着不同方向运动。

分层动画法，就是将运动曲线分解为水平与垂直的运动，元素本身只执行一个方向的运动，其外层容器执行另一方向上的运动。

HTML结构如下：

让container做水平运动，dot做垂直运动，注意两者使用的缓动函数要是不同的，CSS代码如下：

.container {

/* ... 定位等 */

animation: horizontal 2s infinite ease-in;

}

.dot {

/* ... 定位等 */

animation: vertical 2s infinite ease;

}

@keyframes horizontal {

100% {

transform: translateX(150px);

}

}

@keyframes vertical {

50% {

animation-timing-function: ease-in;

transform: translateY(-100px);

}

100% {

transform: translateY(0);

}

}

实现的效果就是简单的抛物线，如下动图：

上例中用到的缓动函数ease和ease-in比较简单，除了简单的缓动函数之外，还可以用贝塞尔曲线函数实现更复杂的曲线运动。

前端工程师需要知道的贝塞尔曲线

大三图形学的时候接触过贝塞尔曲线，后来由于没有实际应用场景，勉强只能模糊的记得公式的样子。如今，贝塞尔曲线在前端领域中也占有一席之地，有了应用场景，学习起来会更有目的性也能理解得更深刻。

贝塞尔曲线的绘制方法

首先，我们需要知道贝塞尔曲线是如何绘制。网上绘制贝塞尔曲线的资料很多，这里推荐参考文献[1]中的扫盲文，介绍的是德卡斯特里奥(de Casteljau)算法，通俗易懂，步骤详实。

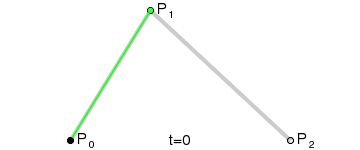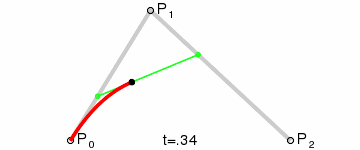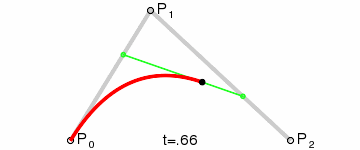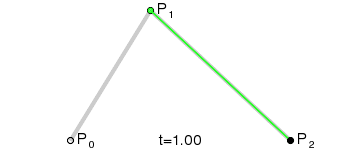
例如，参照下图，ABC三个点作为控制点绘制曲线的大致步骤是：

确定三个辅助点DEF，使其始终满足如下比例关系：

AD:AB = BE:BC = DF:DE

然后将AD:AB的值从0取到1，所有的F所组成的曲线就是ABC三个控制点的二阶贝塞尔曲线。

动图比较直观一点：

前端领域中的贝塞尔曲线

前端领域中动画或过渡的缓动函数就是三阶贝塞尔曲线，即四个控制点的贝塞尔曲线，如下图所示。

如果觉得比较抽象，可以用这个网址 http://myst729.github.io/bezi... ，画四个点观察绘制过程。

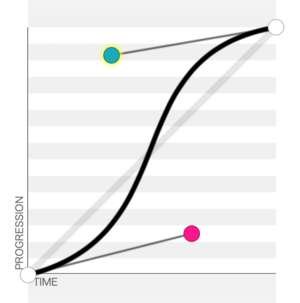
图中有四个控制点，左下方和右上方两个点的位置固定，其坐标为(0,0)与(1,1)。另两个点可移动，坐标分别为红点记为(x1, y1)，绿点记为(x2, y2)。缓动函数中贝塞尔函数是cubic-bezier(x1, y1, x2, y2)，四个参数就是中间两个控制点的坐标。

案例分析

分层动画与贝塞尔曲线联合能够实现一些酷炫的效果，只是我暂时没有找到一个可以精细量化曲线动画的方法，只能粗略确定贝塞尔函数并在细微处调整。

以参考文献[2]中的动画为例，如下图的“what we want”

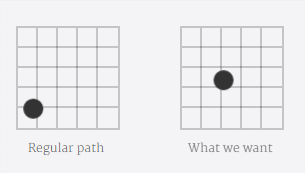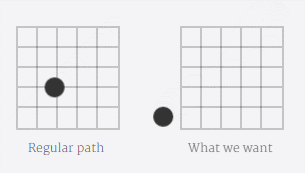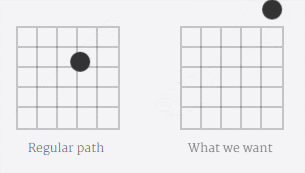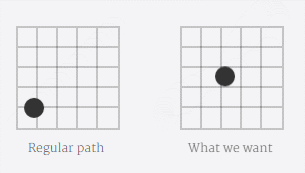
例子中的是对称循环的动画，我们先分析完整动画的一半。

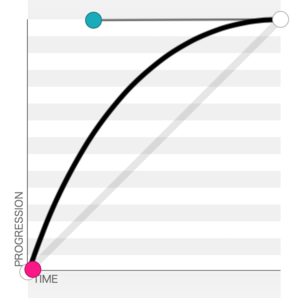
首先看水平方向，位移是translateX(200px)，小黑球水平移动的速率是先快后慢，所以缓动函数应该是如下图的贝塞尔曲线：

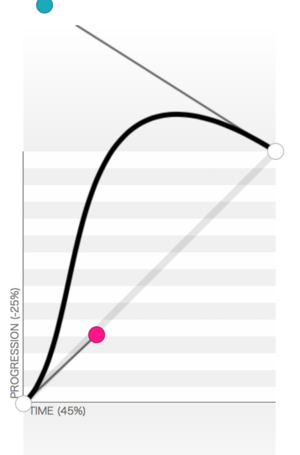
再来看垂直方向，位移是translateY(-200px)，小黑球垂直移动的速率是先缓慢出发，突然快速前进超过终点再缓慢往回，所以缓动函数应该是如下图的贝塞尔曲线：

整体的CSS代码如下：

.container.special {

animation: xAxis 2s infinite cubic-bezier(.02,.01,.26,1);

}

.dot {

animation: yAxis 2s infinite cubic-bezier(.29,.27,.08,1.58);

}

@keyframes xAxis {

50% {

transform: translateX(150px);

}

}

@keyframes yAxis {

50% {

transform: translateY(-150px);

}

}

效果如下图：

可以看出，前一半的动画(左下到右上的过程)与预期实现基本一致。接下来就是处理后一半，后一半的动画就是前一半的镜象对称，也就是前一半的水平方向运动与后一半的垂直方向运动相同，前一半的垂直方向运动与后一半的水平方向运动相同。

.container.special {

animation: xAxis 2s infinite cubic-bezier(.02,.01,.26,1);

}

.dot {

animation: yAxis 2s infinite cubic-bezier(.29,.27,.08,1.58);

}

@keyframes xAxis {

50% {

animation-timing-function: cubic-bezier(.29,.27,.08,1.58); /* 后一半用前一半垂直向上的缓动函数 */

transform: translateX(150px);

}

}

@keyframes yAxis {

50% {

animation-timing-function: cubic-bezier(.02,.01,.26,1); /* 后一半用前一半水平方向上的缓动函数 */

transform: translateY(-150px);

}

}

效果如下图：

参考文档