1.概念
Co-occurrence Histograms of Oriented Gradients(Co-HOG),即共生矩阵梯度方向直方图特征,是一种高维特征,其主要的特点就是引入了共生矩阵。Co-HOG将每个像素点的梯度方向进行成对的组合,同时将原来的梯度方向划分为8个,范围从0度到360度,即每45度为一个bin。由于每两个像素点组成一个组合,所以共生矩阵的大小为8x8=64.梯度方向图及梯度对图如下所示:
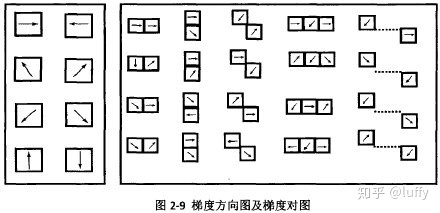
2.点对中的偏移关系
所找点对之间的相对位置,比如上下关系,左右关系等等叫做偏移方式。点对中的偏移关系有31种形式,如图所示,任意一个白点与黑点的组合都是一种偏移方式,同时白点本身也是一种偏移方式。
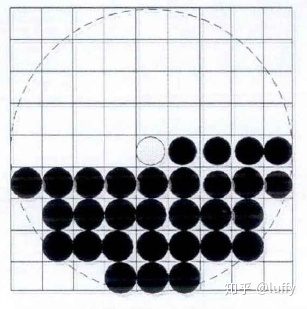
偏移关系总图
所以给定一种偏移方式,我们可视化共生矩阵的过程如下图所示:
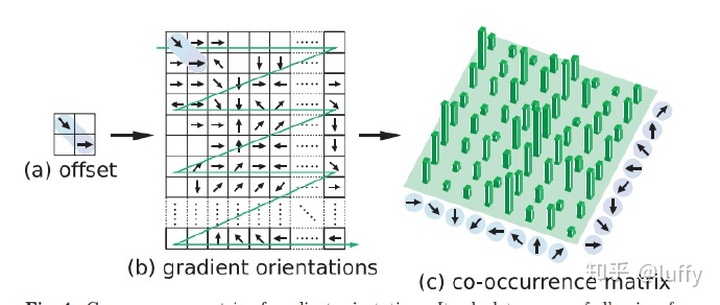
3.Co-HOG特征实现过程
(1)对整幅图像进行和HOG特征一样的梯度计算。然后将图像按照宽高比均分为m*n个小块,例如原图是18x36,那么生成的每个小块为3x6,所以就生成了6*6个小块(小块是无重叠区域的);
(2)选定一种偏移方式对每个小块进行扫描,生成一个共生矩阵,这样就会生成一个m*n*64的列向量;
(3)然后变换一种偏移关系在整幅图像上扫描,直到31种所有偏移方式都扫描一次。这样将会生成31*64*m*n的列向量,也就是最终的Co-HOG特征。
那么整个Co-HOG特征的计算过程如下图所以:
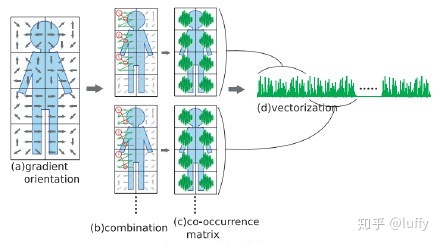
4.Co-HOG特征的优势
Co-HOG特征与HOG特征一样,在光照变化和形变下具有鲁棒性,除此之外,由于CO-HOG特征是高维特征,因此它更加细化地表达了图像形状的信息。我们知道HOG特征在计算上包括更多的复杂步骤,例如方向权值投票,梯度方向直方图归一化,还有小区域是重叠的,而Co-HOG却不需要这些步骤,所以计算速度更快。
5.Co-HOG特征计算实现的伪代码








 Co-HOG(共生矩阵梯度方向直方图)是一种高维特征,它通过引入共生矩阵来细化表达图像形状信息。该特征计算过程包括梯度计算、小块划分、共生矩阵生成等步骤,并具有较好的鲁棒性和计算效率。
Co-HOG(共生矩阵梯度方向直方图)是一种高维特征,它通过引入共生矩阵来细化表达图像形状信息。该特征计算过程包括梯度计算、小块划分、共生矩阵生成等步骤,并具有较好的鲁棒性和计算效率。
















 2300
2300

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








