博客介绍了利用圆的相切相交相离公式解决高考数学中圆锥曲线问题的方法，通过椭圆、双曲线、抛物线的焦半径定理，提供例题和证明，强调解析几何结合几何性质的重要性。
周末上课时，一个学生问了我这样一个圆锥曲线问题。
他说这道题做了很久，并没有什么明确的思路，也尝试了几种方法，但是不是很奏效，甚至现在对解析几何很有抵触情绪。当我读完这道题，几秒钟之后，便问他这道题的答案是不是4？学生很惊讶的看着我，并且问我：“老师，这道题你是不是做过？”我说没有做过，但是这道题有相应的结论，我不仅能秒做这道题，同时如果把此题改成双曲线也有类似的结论，今天就借着这道题为开始，简单聊一聊圆锥曲线中的某些特定的结论。
很多人认为，解析几何中的运算量大，不仅耗费时间，而且难以保证正确率。这是一个非常错误的观点。
解析几何，首先是几何问题，一味强调解析几何中的代数运算，有时会导致繁琐的运算过程，必要时要综合考虑几何因素，即在用代数方法研究曲线间关系的同时，充分好利用图形本身所具有的平面几何性质长可得到简洁而优美的解法。
由于解析几何题，综合性强，运算繁杂，很多学生极易产生畏惧心理，考试时甚至采取放弃的策略，从而平时也不重视解析几何的复习，导致放弃了一些在能力范围内的题，实在可惜。
老师根据一类解析几何中的几何性质，总结了一些小定理，希望起到抛砖引玉的作用。
定理：
1.椭圆以焦半径为直径的的圆必与长轴为直径的圆(此圆与椭圆内切)相切
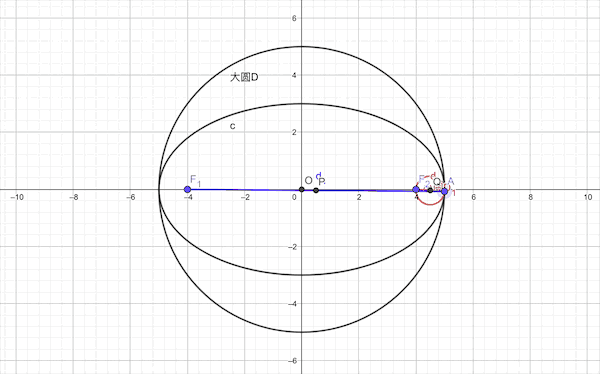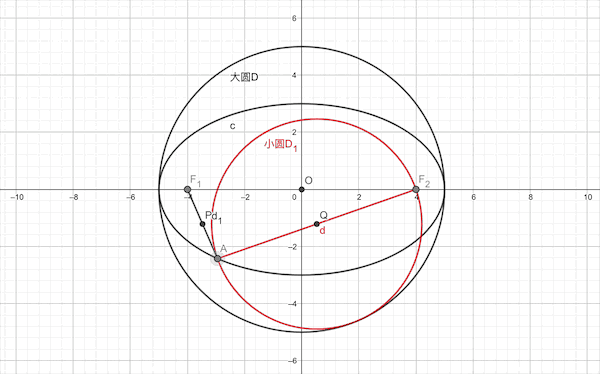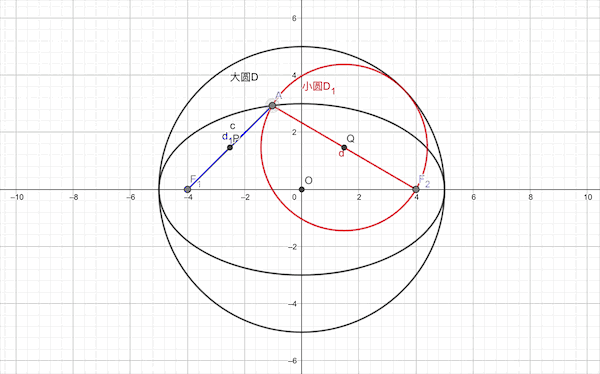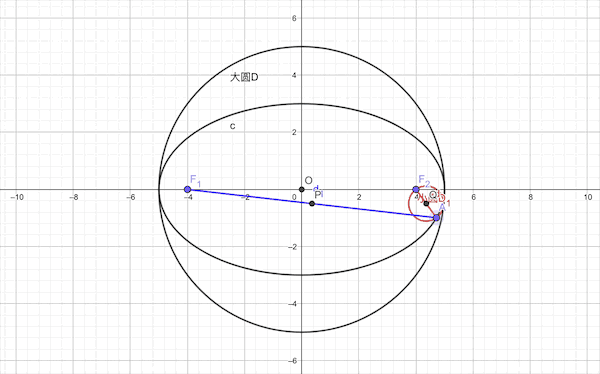
2.双曲线以焦半径为直径的的圆必与实轴为直径的圆(此圆与椭圆内切)相切
3.抛物线以焦半径为直径的的圆必与顶点处的切线相切(此切线可以看做半径无穷大的圆)
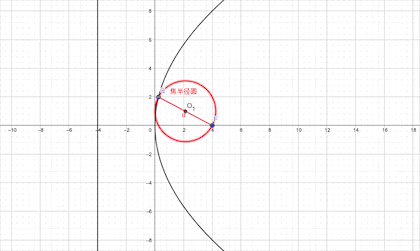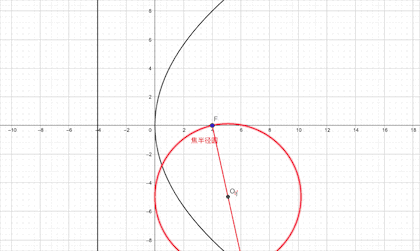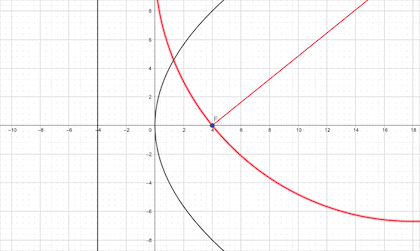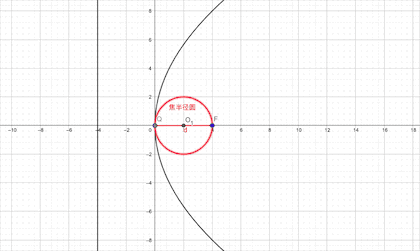
下面是证明：以椭圆为例证明，其他的证明希望同学们自行完成。有助于对该结论的理解和应用。
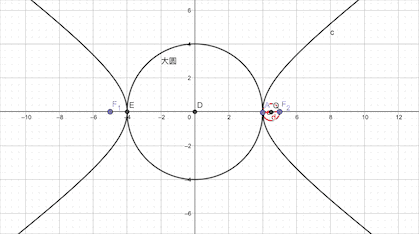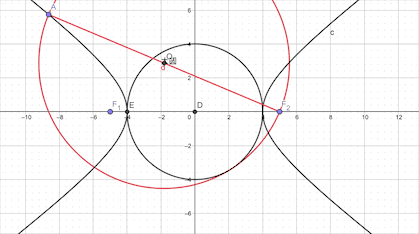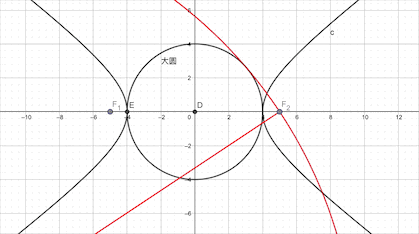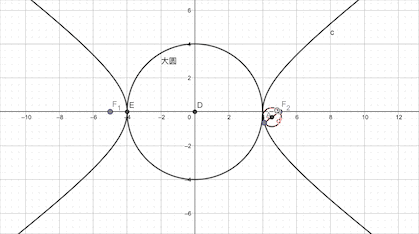
例题：椭圆以焦半径为直径的的圆必与长轴为直径的圆(此圆与椭圆内切)相切。
这里不妨先建一个坐标系，同样的，不妨设椭圆的焦点在x轴上，左右顶点为CD两点。且它的左右焦点为F1和F2，椭圆上一个动点A，以AF2为直径做圆Q，以CD为直径的圆为圆O，求证：圆Q与圆O相切。
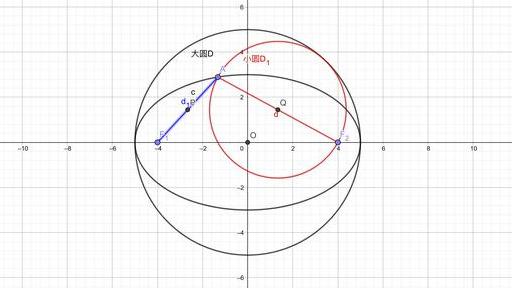
以下是证明过程：
评注：解析几何问题，实质就是平面几何，坐标化，所以节解析几何问题时必要的平面几何知识，对解题很有帮助，这一点希望大家在训练中加以体会。
有了这几个结论，相信下面的几个问题就可以轻易的解决了！
例题1
根据本文的动图，可以轻易看出答案应该是B。
例题二
显然答案是A
例题三
由本文的第一个动图，可以看出来，当点P沿椭圆移动一周时，圆M完全可以覆盖整个大圆，故本题的动圆所覆盖的平面区域形状是以O为圆心，a为半径的圆，面积自然是πa²。
下面在回到本文开端的题目：
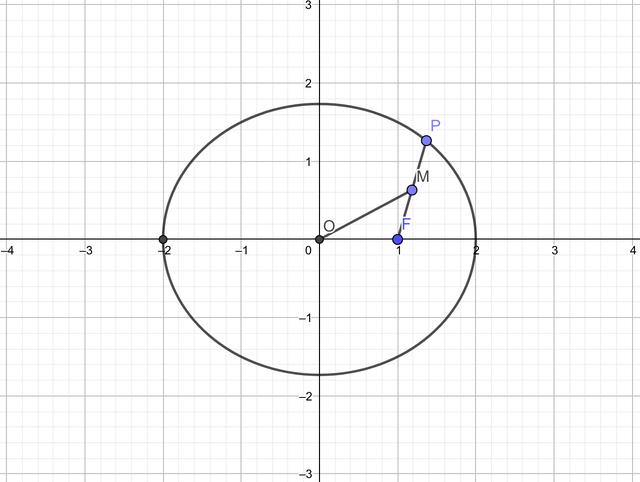
我们不妨用这个结论，OM+红色的线等于半径R，而红色的线又等于MF和PM，所以OM+MF=R，2OM+2 MF=2a，也就是本题的2OM+PF=2a=4。当然这题可以秒杀！
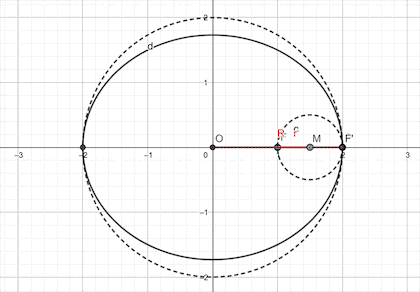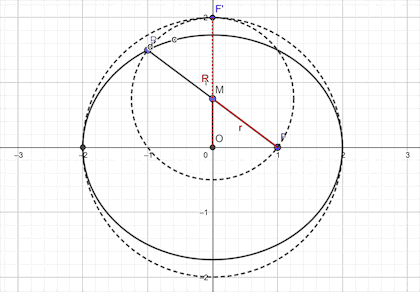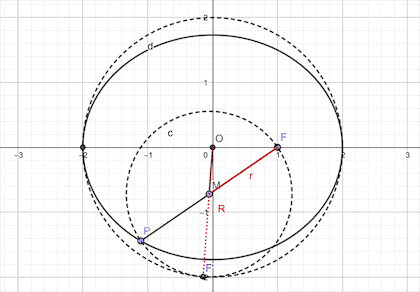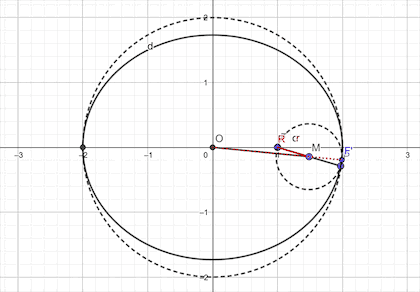
这三个结论又很巧妙地将椭圆，双曲线和抛物线紧紧地联系在一起，然而，事实上，对于该结论的应用，椭圆和双曲线要求的并不高，重点是在抛物线上。因为高中数学更讲究的是精准，对于相离和相交两种情况，考察的并不多，相切的情况却永远是重点。所以对于抛物线的结论应该给予足够的重视。
下面补充一道练习题
分析：依题意只以抛物线的焦半径PF为直径的圆与y轴相切。故此题选C
扫一扫
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
