红黑树算法--插入

#include <iostream>
#define NULLVAL -1

using namespace std;

bool BLACK = true;
bool RED = false;
 
class RBTree {
	public:
		RBTree* left;
		RBTree* right;
		float val;
		bool color;
		RBTree* parent;
		RBTree() {
			left = NULL;
			right = NULL;
			val = NULLVAL;
			color = BLACK;
			parent = NULL;
		}
		RBTree(float value, bool colr) {
			left = NULL;
			right = NULL;
			val = value;
			color = colr || RED;
			parent = NULL;
		}
}; 

void PrintChilds(RBTree* node) {
	if (node == NULL) {
		cout << "node为NULL" << endl;
		return; 
	}
	if (node->parent != NULL) {
		cout << "节点 " << node->val << "的父节点的值为: " << node->parent->val << "    颜色为： " << (node->parent->color ? "BLACK" : "RED")  << endl; 
	} else {
		cout << "节点 " << node->val << "的父节点值为空" << endl;
	} 
	/**
	if(node->left != NULL) {
		cout << "节点 " << node->val << "的左子树值为: " << node->left->val << "    颜色为： " << (node->left->color ? "BLACK" : "RED") << endl; 
	} else {
		cout << "节点 " << node->val << "的左子树值为空" << endl;
	}
	if(node->right != NULL) {
		cout << "节点" << node->val << "的右子树值为: " << node->right->val << "    颜色为： " << (node->right->color ? "BLACK" : "RED") << endl; 
	} else {
		cout << "节点 " << node->val << "的右子树值为空" << endl; 
	}
	*/
} 

//添加子树 
RBTree* setChildTree(RBTree* &node, char direct, float value, bool color) {
	if (node == NULL) return NULL;
	RBTree* child = new RBTree(); 
	child->parent = node;
	child->color = color;
	child->val = value;
	if(direct == 'r') node->right = child;
	else node->left = child;
	return child;
}

//查询一个节点的父节点
RBTree* ParentOf(RBTree* node) {
	return (node == NULL) ? NULL : node->parent; 
}

//查询一个节点的叔叔节点
RBTree* UncleOf(RBTree* node) {
	//先找到该节点的爷爷节点
	//然后判断该节点的父节点是爷爷节点的左子树还是右子树
	RBTree* father = ParentOf(node);
	RBTree* grand = ParentOf(father);
	if (grand == NULL) return NULL;
	if (father == grand->left) {
		return (grand->right == NULL) ? NULL : grand->right; 
	} else if (father == grand->right){
		return (grand->left == NULL) ? NULL : grand->left;
	} else {
		return NULL;
	}
}

//更改节点颜色
void SetColor(RBTree* node, bool color) {
	node->color = color;
}

//查询一个节点的左子节点
RBTree* LeftChildOf(RBTree* node) {
	if(node == NULL) return NULL;
	return node->left;
}

//查询一个节点的右子节点
RBTree* RightChildOf(RBTree* node) {
	if(node == NULL) return NULL;
	return node->right;
}

//节点的左旋
void LeftRotation(RBTree* &root, RBTree* node) {
	if(node == NULL) return;
	if(node->right == NULL) return;
	RBTree* father = node->parent;
	RBTree* nodeRight = node->right;
	//处理nodeRight的左子树
	if (nodeRight->left == NULL) {
		node->right = NULL;
	} else {
		node->right = nodeRight->left;
		nodeRight->left->parent = node;
	}
	//处理node的原来的父节点
	if(father == NULL) {
		nodeRight->parent = NULL;
		root = nodeRight;
	} else {
		nodeRight->parent = father;
		if(father->left == node) {
			father->left = nodeRight;
		} else {
			father->right = nodeRight;
		}
	}
	//处理nodeRight新的左子树
	nodeRight->left = node;
	node->parent = nodeRight;
}

//节点的右旋
void RightRotation(RBTree* &root, RBTree* node) {
	if(node == NULL) return;
	if(node->left == NULL) return;
	
	RBTree* father = node->parent;
	RBTree* nodeLeft = node->left;
	//处理nodeLeft的右子树
	if(nodeLeft->right == NULL) {
		node->left = NULL;
	} else {
		node->left = nodeLeft->right;
		nodeLeft->right->parent = node; 
	}
	
	//处理father和nodeLeft的关系
	if(father == NULL) {
		nodeLeft->parent = NULL;
		root = nodeLeft;
	} else {
		nodeLeft->parent = father;
		if(father->left == node) {
			father->left = nodeLeft;
		} else {
			father->right = nodeLeft;
		}
	}
	
	//处理node和nodeLeft的关系
	node->parent = nodeLeft;
	nodeLeft->right = node;
}


void InOrder(RBTree* root) {
	if(root != NULL) {
		InOrder(root->left);
		//cout << "输出根节点： " << root->val << endl;
		PrintChilds(root);
		InOrder(root->right);  
	}
}

/**
 1.2-3-4树：新增元素 + 2节点合并(节点中只有一个元素)=3节点(节点中有两个元素)
    红黑树：新增一个红色节点 + 黑色父亲节点 = 上黑下红(2节点)
 
 2.2-3-4树：新增元素 + 3节点合并(节点中有两个人元素)=4节点(节点中有三个元素) 
 	这里有四种情况（左3,右3,有两个左中右不需要调整） 
 	红黑树：新增一个红色节点+上黑下红=排序后中间节点为黑，两边节点为红

 3.2-3-4树：新增一个元素 + 4节点合并=原来的4节点分裂，中间元素升级为父节点，新增元素与剩下的其中一个合并
 	 红黑树：新增红色节点+爷爷节点黑，父节点和叔叔节点都是红色=爷爷节点变红，父亲和叔叔节点变黑，如果爷爷节点是根节点，爷爷节点变黑 
 */

/**这种方法不好，退出之后栈中还有压入的函数调用=>耗内存 
void InsertStack(RBTree* root, float dat) {
	if(dat < root->val) {
		if(root->left != NULL) {
			InsertStack(root->left, dat);
		} else {
			setChildTree(root, 'l', dat, RED);
		}
	} else {
		if(root->right != NULL) {
			InsertStack(root->right, dat);
		} else {
			setChildTree(root, 'r', dat, RED);
		}
	}	
}
*/

/**将节点node插入root中，这是一种father不好处理的写法 
void InsertFalse(RBTree* root, float dat) {
	//如果在空节点处插入
	if(root == NULL) {
		root = new RBTree;
		root->color = BLACK;
		root->val = dat;
		root->left = NULL;
		root->right = NULL;
		root->parent = NULL;
	} else {
		//如果在非头节点的左右子树插入 
		RBTree* father = NULL;
		RBTree* temp = root; 
		
		while(temp != NULL) {
			//father = temp->parent; //如果父节点设置在这个位置，最后一次无法更新，实际上是爷爷节点 
			if(dat < temp->val) {
				temp = temp->left;
			} else {
				temp = temp->right;
			}
			//father = temp->parent; //如果在这个地方设置父节点,最后一次更新的temp=NULL,无法追溯到父节点 
		}
		cout << "父节点为" << father->val << endl;
			
	}
}
*/

//node是插入的节点，要调整其父节点，叔叔节点和其他节点 
void fixPosition(RBTree* root, RBTree* node) {
	if(node == NULL) return;
 	//第一种情况,如果node的父节点为NULL
 	if(node == root) return;
 	//第二种情况,如果node的父节点为黑
 	if(node->parent->color == BLACK) return;
 	//第三种情况,如果node的父节点为红
	while(node != NULL && node != root && node->parent->color == RED) {
		if(UncleOf(node) == NULL) {
   			bool lr1, lr2;
   			lr1 = ParentOf(ParentOf(node))->left == ParentOf(node);
   			lr2 = ParentOf(node)->left == node;
   			if(lr1 && lr2) {
    			//如果是左3直线,以node的爷爷节点为基点右旋
    			RightRotation(root, ParentOf(ParentOf(node)));
    			SetColor(ParentOf(node), BLACK);
    			SetColor(ParentOf(node)->right, RED);
   			} else if(lr1 && !lr2) {
    			//如果是左3折线
    			LeftRotation(root, ParentOf(node));
    			RightRotation(root, ParentOf(node));
    			SetColor(node, BLACK);
    			SetColor(node->right, RED);
   			} else if(!lr1 && lr2) {
    			//如果是右3折线
    			RightRotation(root, ParentOf(node));
    			LeftRotation(root, ParentOf(node));
    			SetColor(node, BLACK);
    			SetColor(node->left, RED);
   			} else {
    			//如果是右3直线
    			LeftRotation(root, ParentOf(ParentOf(node)));
    			SetColor(ParentOf(node), BLACK);
    			SetColor(ParentOf(node)->left, RED);
   			} 
  		} else {
  		//如果是4节点转化过来的情况
       		//需要统一更换父叔节点的颜色和爷爷节点的颜色
      		SetColor(ParentOf(node), BLACK);
      		SetColor(UncleOf(node), BLACK);
      		SetColor(ParentOf(ParentOf(node)), RED);
      		//递归循环,将爷爷节点视作node重新判断 
      		node = ParentOf(ParentOf(node));
  		}
	}
	SetColor(root, BLACK);
}

void Insert(RBTree* root, float dat) {
	if(root == NULL) {
		root = new RBTree(dat, BLACK);
		return;
	}
	RBTree* father = NULL;
	RBTree* temp = root; 
	RBTree* nnode = NULL;
	while(temp != NULL) {
		father = temp; //不再更新的时候,就是本节点,不在考虑父节点的问题 
		if(dat < temp->val) {
			temp = temp->left;
		} else {
			temp = temp->right;
		}
	}
	if(dat < father->val) {
		nnode = setChildTree(father, 'l', dat, RED);
	} else {
		nnode = setChildTree(father, 'r', dat, RED);
	}
	fixPosition(root, nnode);
}

int main() {
	RBTree* root = new RBTree(7, BLACK);
	setChildTree(root, 'l', 3, RED);
	setChildTree(root, 'r', 10, RED);
	setChildTree(root->left, 'l', 2, BLACK);
	setChildTree(root->left, 'r', 5, BLACK);
	setChildTree(root->right, 'l', 8, BLACK);
	setChildTree(root->right, 'r', 11, BLACK);
	setChildTree(root->left->left, 'l', 1, RED);
	setChildTree(root->left->right, 'l', 4, RED);
	setChildTree(root->left->right, 'r', 6, RED);
	setChildTree(root->right->left, 'r', 9, RED);
	setChildTree(root->right->right, 'r', 12, RED);
	
	Insert(root, 0.5);
	Insert(root, 1.5);
	Insert(root, 4.5);
	InOrder(root);
	return 0; 
}
 

• 原则
  • 上黑下红(🌂)
  • 新插入的节点必须是红色
  • 一个红色节点的两个子节点必须是黑色
  • 根节点是黑色节点
  • 不能有连续的两个红色节点
  • 注意附加情况中的递归问题(将此节点的爷爷节点 赋值给 此节点，while循环)

<一> 2-3-4树，2节点(单元素)对应红黑树的插入前图像

插入后的图象

<二> 2-3-4树，3节点(双元素)对应红黑树的插入前图象

插入后的图象

调整后的图象

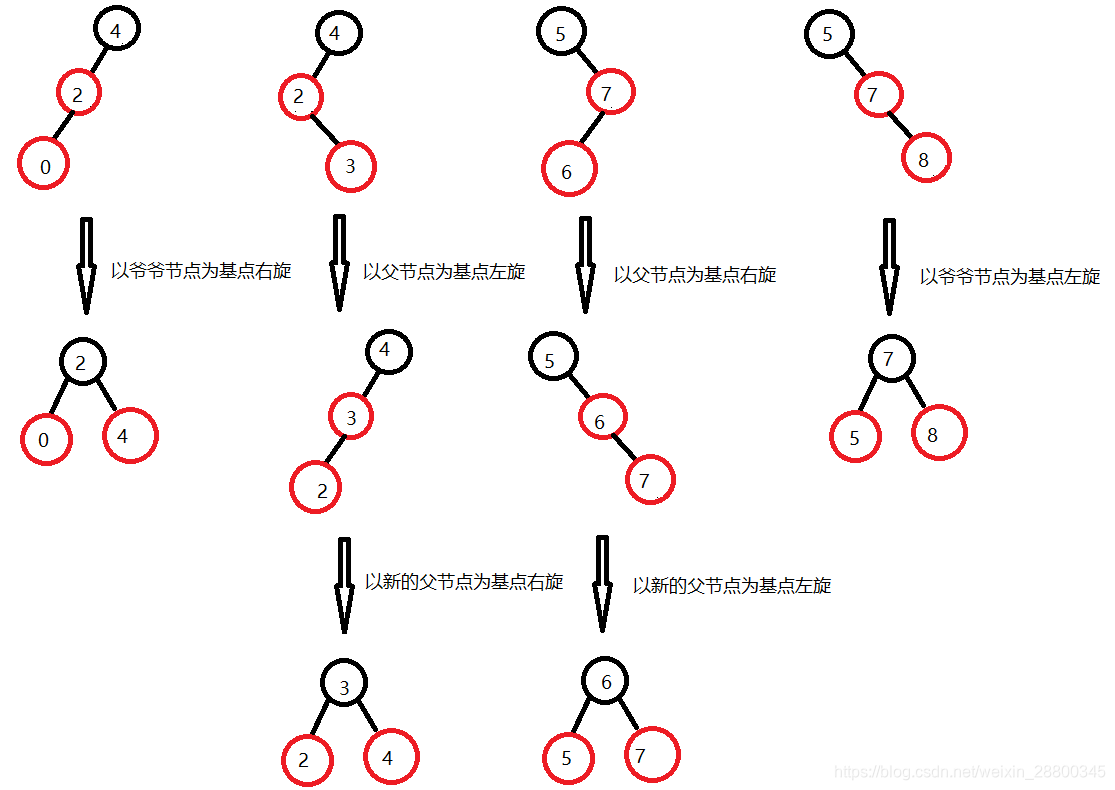
<三> 2-3-4树，4节点(三元素)对应红黑树的插入前图象

插入后的图象

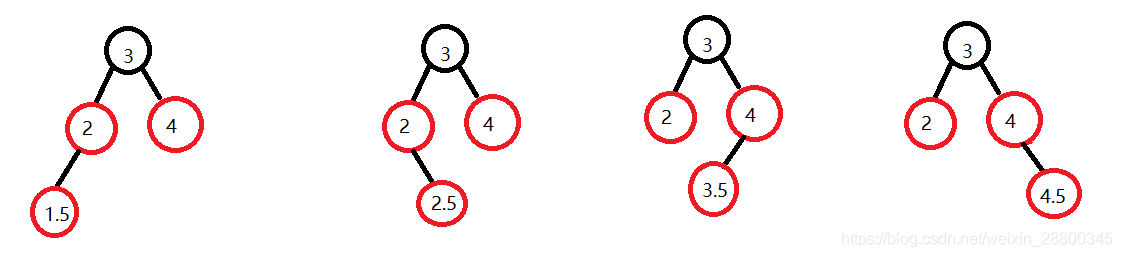
调整后的图象(父节点和叔叔节点变黑，爷爷节点变红)

需要递归的情况

• 调整完的图象如果是下边这种情况，需要递归