计算机图形学中几何变换的定义,计算机图形学 实验7 三维几何变换（MFC中）

实验目的：

理解几何变换的意义

掌握三维基本几何变换的算法

实验内容：

实验步骤：

在本次试验中，我们实现透视投影和三维几何变换。我们首先定义一个立方体作为我们要进行变换的三维物体。

定义顶点表和面表的数据结构

定义三维坐标点的结构，面的结构：

定义顶点表保存立方体顶点信息

顶点 x坐标 y坐标 z坐标

V0 x0＝-a y0＝-a z0＝-a

V1 x1＝ a y1＝-a z1＝-a

V2 x2＝ a y2＝ a z2＝-a

V3 x3＝-a y3＝ a z3＝-a

V4 x4＝-a y4＝-a z4＝ a

V5 x5＝ a y5＝-a z5＝ a

V6 x6＝ a y6＝ a z6＝ a

V7 x7＝-a y7＝ a z7＝ a

定义面表保存面的信息：

面 第一个顶点 第二个顶点 第三个顶点 第四个顶点 说明

F0 4 5 6 7 前面

F1 0 3 2 1 后面

F2 0 4 7 3 左面

F3 1 2 6 5 右面

F4 2 3 7 6 顶面

F5 0 1 5 4 底面

立方体参数中的a=100，即立方体的边长为200，给出下面代码：

立方体顶点表的定义代码：

CPOINT3 V[8];// 定义立方体

void setPoint();//定义立方体顶点坐标

void CTransformView::setPoint()//设置立方体顶点坐标

{

float a = 100;

V[0].x = -a; V[0].y = -a; V[0].z = -a;

V[1].x = a; V[1].y = -a; V[1].z = -a;

V[2].x = a; V[2].y = a; V[2].z = -a;

V[3].x = -a; V[3].y = a; V[3].z = -a;

V[4].x = -a; V[4].y = -a; V[4].z = a;

V[5].x = a; V[5].y = -a; V[5].z = a;

V[6].x = a; V[6].y = a; V[6].z = a;

V[7].x = -a; V[7].y = a; V[7].z = a;

}

立方体面表的定义代码：

CFace F[6];//六个面

void setFace();//设置立方体每个面的信息

void CTransformView::setFace()//设置立方体每个面里的信息

{

F[0].SetNum(4); //前面

F[0].VI[0] = 4; F[0].VI[1] = 5; F[0].VI[2] = 6; F[0].VI[3] = 7;

F[1].SetNum(4); //后面

F[1].VI[0] = 0; F[1].VI[1] = 3; F[1].VI[2] = 2; F[1].VI[3] = 1;

F[2].SetNum(4);//左面

F[2].VI[0] = 0; F[2].VI[1] = 4; F[2].VI[2] = 7; F[2].VI[3] = 3;

F[3].SetNum(4);//右面

F[3].VI[0] = 1; F[3].VI[1] = 2; F[3].VI[2] = 6; F[3].VI[3] = 5;

F[4].SetNum(4);//上面

F[4].VI[0] = 2; F[4].VI[1] = 3; F[4].VI[2] = 7; F[4].VI[3] = 6;

F[5].SetNum(4);//下面

F[5].VI[0] = 0; F[5].VI[1] = 1; F[5].VI[2] = 5; F[5].VI[3] = 4;

}

定义函数实现三维变换的矩阵运算

函数代码：

class CChangForm

{

public:

CChangForm();

~CChangForm();

void Identity();//变换矩阵初始化

void SetMat(CPOINT3 *p, int n);//传入所需变换的点

void MultMat();//矩阵相乘

};

void CChangForm::MultMat()//矩阵相乘

{

CPOINT3 *NewP = new CPOINT3[VNum];//用于记录矩阵计算结果

for (int i = 0; i < VNum; i++)

{

NewP[i].x = P01d[i].x * T[0][0] + P01d[i].y * T[1][0] + P01d[i].z * T[2][0] + P01d[i].c * T[3][0];

NewP[i].y = P01d[i].x * T[0][1] + P01d[i].y * T[1][1] + P01d[i].z * T[2][1] + P01d[i].c * T[3][1];

NewP[i].z = P01d[i].x * T[0][2] + P01d[i].y * T[1][2] + P01d[i].z * T[2][2] + P01d[i].c * T[3][2];

NewP[i].c = P01d[i].x * T[0][3] + P01d[i].y * T[1][3] + P01d[i].z * T[2][3] + P01d[i].c * T[3][3];

P01d[i].x = NewP[i].x;

P01d[i].y = NewP[i].y;

P01d[i].z = NewP[i].z;

P01d[i].c = NewP[i].c;

}

delete[]NewP;//释放内存

NewP = NULL;

}

定义函数实现三维形体的绘制，根据面表和投影变换后的顶点表进行三维形体绘制。

函数代码：

void DrawObject(CDC* pDC);

void CTransformView::DrawObject(CDC* pDC)

{

int FaceNum, PointNum;//面和边的循环控制变量

CCP2 pt, PT;

//绘制立体图形

for (FaceNum = 0; FaceNum < 6; FaceNum++)

{

for (PointNum = 0; PointNum < 4; PointNum++)

{

pt = Project(Key, V[F[FaceNum].VI[PointNum]]);

if (PointNum == 0)

{

PT = pt;

pDC->MoveTo(pt.x, pt.y);

}

else

pDC->LineTo(pt.x, pt.y);

}

pDC->LineTo(PT.x, PT.y);

}

}

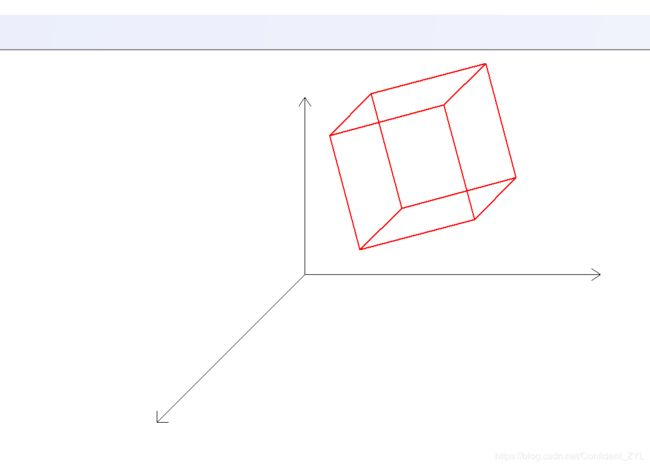
在OnDraw()中实现将立方体围绕z轴旋转15°，然后沿x，y轴各平移200,200。

sin(15°) = 0.25881904510252 cos(15°) = 0.96592582628907

旋转矩阵的定义代码：

void Rotate(char c, double angle);//旋转

void CChangForm::Rotate(char c = ‘Z’, double angle = 0)//旋转

{

Identity();

switch (c)

{

case 'X'://绕X轴旋转

T[1][1] = cos(angle / 180 * PI);

T[1][2] = sin(angle / 180 * PI);

T[2][1] = -sin(angle / 180 * PI);

T[2][2] = cos(angle / 180 * PI);

break;

case 'Y'://绕Y轴旋转

T[0][0] = cos(angle / 180 * PI);

T[0][2] = -sin(angle / 180 * PI);

T[2][0] = sin(angle / 180 * PI);

T[2][2] = cos(angle / 180 * PI);

break;

case 'Z'://绕Z轴旋转

T[0][0] = cos(angle / 180 * PI);

T[0][1] = sin(angle / 180 * PI);

T[1][0] = -sin(angle / 180 * PI);

T[1][1] = cos(angle / 180 * PI);

break;

}

MultMat();

}

平移矩阵的定义代码：

void Move(double x, double y, double z);//平移(变换函数)

void CChangForm::Move(double x = 0, double y = 0, double z = 0)//移动(变换函数)

{

Identity();

T[3][0] = x;

T[3][1] = y;

T[3][2] = z;

MultMat();

}

完成全部变换并绘制结果的代码：

void CTransformView::OnDraw(CDC* pDC)

{

CTransformDoc* pDoc = GetDocument();

ASSERT_VALID(pDoc);

if (!pDoc)

return;

CRect rect;//定义矩形

GetClientRect(&rect);//获得客户区大小

pDC->SetMapMode(MM_ANISOTROPIC);//设置映射模式

pDC->SetWindowExt(rect.Width(), rect.Height());//设置窗口范围

pDC->SetViewportExt(rect.Width(), -rect.Height());//设置窗视区范围

pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2);//设置客户区中心为坐标轴(视区)原点

rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2);//客户区矩形矫正

pDC->MoveTo(0, 0); pDC->LineTo(500, 0);//{画出坐标轴}

pDC->MoveTo(0, 0); pDC->LineTo(0, 300);

pDC->MoveTo(0, 0); pDC->LineTo(-250, -250);

pDC->MoveTo(-10, 285); pDC->LineTo(0, 300);

pDC->MoveTo(10, 285); pDC->LineTo(0, 300);

pDC->MoveTo(485, 10); pDC->LineTo(500, 0);

pDC->MoveTo(485, -10); pDC->LineTo(500, 0);

pDC->MoveTo(-250, -250); pDC->LineTo(-250, -230);

pDC->MoveTo(-250, -250); pDC->LineTo(-230, -250);

CPen NewPen, *P01Pen;//设置新画笔

NewPen.CreatePen(PS_SOLID, 2, RGB(255, 0, 0));//设置画笔属性

P01Pen = pDC->SelectObject(&NewPen);//应用新画笔

DrawObject(pDC);

pDC->SelectObject(P01Pen);//恢复画笔

NewPen.DeleteObject();//释放画笔

// TODO: 在此处为本机数据添加绘制代码

}

switch (nChar)

{

//平移

case ‘D’:t.Move(200, 0, 0); break;//沿X轴平移

case ‘A’:t.Move(-200, 0, 0); break;

case ‘W’:t.Move(0, 200, 0); break;//沿Y轴平移

case ‘S’:t.Move(0, -200, 0); break;

case ‘Q’:t.Move(0, 0, 200); break;//沿Z轴平移

case ‘E’:t.Move(0, 0, -200); break;

//旋转

case’J’:t.Rotate(‘X’, 15); break;//绕X轴逆时针旋转

case’K’:t.Rotate(‘Y’, 15); break;//绕Y轴顺时针旋转

case’L’:t.Rotate(‘Z’, 15); break;//绕Z轴顺时针旋转

}

结果图：