监督学习——回归

回归是有达尔文表弟提出的，这个梗想了解的可以自己查，他说‘回归’反映了系统的随机运动总是趋向于其整体运动规律的趋势。

以下将介绍：

（1）线性回归

（2）二分类：Logistic回归

（3）多分类：Softmax回归

（4）广义线性模型

1.1.1.1. 线性回归

线性回归就是用一个超平面去拟合样本点的标签：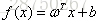

对于一维的情况，就是用一条直线去拟合样本点，为方便把偏置b记到权重向量中，。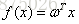

1.求解

回归任务，常用的损失函数为平方损失函数，对应的经验风险就是均方误差（MSE）：

 

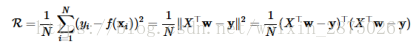
y表示训练样本的真是标签。

 

解一：正规方程组：直接用R的一阶导数等于0求极值：

 

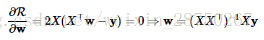
就是最小二乘法（Ordinary Least Squares，OLS）解方程 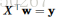。值得注意的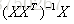是其实就是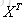的伪逆，计算伪逆的复杂度很高。

需要注意一个问题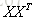：需要是可逆矩阵，也就是说每维特征之间线性无关，才可以求得唯一解。当其不可逆（特征个数比样本个数还要多）时，解不唯一，需要用梯度下降（Gradient descent）来迭代求解。

解二：最小均方误差（LMS），用梯度下降法求解，梯度：

 

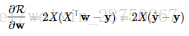
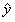表示模型的输出标签，y表示真实的标签。

这样的方式是每更新一次参数就要计算整个训练集上的梯度，是批梯度下降（batch GD）；

如果把这个过程拆成 NN 次，也就是每次只随机挑选一个样本计算梯度，就是随机梯度下降（Stochastic GD，SGD）。

还有一种是mini-batch梯度下降，每次挑选一个小批量样本计算梯度。整个训练集计算完一次梯度称为“一轮”。

1.1.1.2. Logistic回归

先使用logistic函数 σ(z) 将 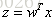从实数空间 (−∞,+∞)映射到概率空间 (0,1) 上，可以将映射之后的值 σ(z) 解释为样本 x 属于正类（记类别标记为1）的可能性，也就是后验概率的估计值：

 

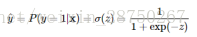
 既然解释成后验概率，然后就可以给出分类规则（最大后验概率决策）：当 P(y=1|x)>0.5，认为样本 x属于正类；否则样本 x属于正类属于负类。

Logistic回归模型：

 

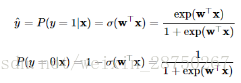
其实就是线性回归加了一层激活函数。

线性回归是用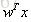去拟合 y；二项Logistic回归则是去拟合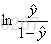，换句话说就是在拟合对数几率（log-odds，几率是样本属于正类的可能性与属于负类的可能性的比值）。也就是说，二项Logistic回归在对对数几率做回归，进而转化为解决分类问题。

求解：对数似然函数为：

 

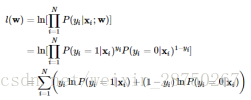
损失函数通过最小化负的对数似然函数得到：

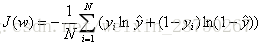
其实括号里的意思就是（1*ln（P(1|x)）+0*ln(P(0|x))）

   由于优化目标求不出解析解，但它是高阶连续可微的凸函数，所以可以用迭代的方法，如梯度下降法（GD）。

      因为SGD每次迭代是随机选择一个样本，所以这里先求取模型对一个样本的损失的梯度：

 

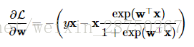
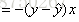
这个梯度形式和线性回归是一样的。

1.1.1.3. Soft-max回归

Logistic回归损失函数，假设函数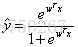：，损失函数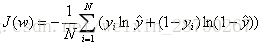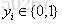：，；重新损失函数：

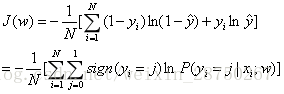
Soft-max损失函数为：

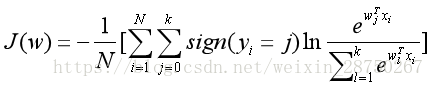
多分类问题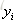样本类别标签不再是0和1，可以是k个不通的值；

那么，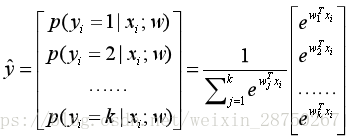

1.1.1.4. 广义线性模型

经典线性模型自变量的线性预测就是因变量的估计值。 广义线性模型：自变量的线性预测的函数是因变量的估计值。常见的广义线性模型有：probit模型、Poisson模型、对数线性模型等等。对数线性模型里有：logistic regression、Maximum entropy。

对于线性回归，求解参数w即可，可以用解析解的方法求解，也可以用梯度下降的方式求解。

对于Logistic回归和Soft-max回归，推导及求解方式相同。基本遵循以下步骤：

1. 给出分类概率函数

2. 求累加的似然函数

3. 转换为对数似然函数求驻点

4. 利用梯度下降法求解。