小波变换系数计算实例_超全超实用的Matlab小波分析函数总结

函数名	函数表示	格式	释义
一维连续小波变换	cwt	coefs=cwt(s,scales,'wavename')coefs=cwt(s,scales,'wavename','plot')	s:一维连续信号；scales:尺度向量，可以为离散值，表示为[a1,a2,a3……]，也可为连续值，表示为[amin:step:amax]；wavename：小波名称
单尺度一维离散小波变换	dwt	1. [cA,cD]=dwt(X,'wavename') 2. [cA,cD]=dwt(X,Lo_D,Hi_D) 3. [cA,cD]=dwt(X,'wavename',‘mode’,MODE) 4. [cA,cD]=dwt(x,Lo_D,Hi_D,‘mode’,MODE)	用于信号的单层分解的一维离散小波变换： 1. 使用指定的小波基函数 'wname' 对信号 X 进行分解。cA、cD 分别为近似分量和细节分量； 2. 使用指定的滤波器组 Lo_D (低通滤波器)、 Hi_D(高通滤波器) 对信号进行分解。 3. 4.MODE表示指定信号的扩展方式。
单尺度一维离散小波逆变换	idwt	1. X=idwt(cA,cD, 'wname' ) 2. X=idwt(cA,cD,Lo_R, Hi_R) 3. X=idwt(cA,cD, 'wname' ,L) 4. X=idwt(cA,cD, Lo_R, Hi_R, L)	1. 由近似分量cA和细节分量cD经小波反变换重构原始信号X。 2. 用指定的重构滤波器 Lo_R(低通滤波器) 和 Hi_R (高通滤波器)经小波反变换重构原始信号X。 3. 4. 指定返回信号 X 中心附近的 L 个点。
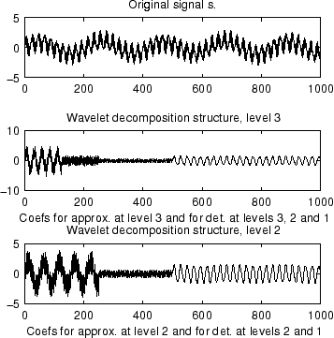
单尺度一维小波的重构	upwlev	1. [NC,NL,cA]=upwlev(C,L,'wname')2. [NC,NL,cA]=upwlev(C,L,Lo_R,Hi_R)	返回上一尺度的分解结构并提取最后一尺度的低频分量，等价于[C,L]=wavedec(x,N-1，'wavename')，图2主要程序[c,l] = wavedec(s,3,'db1'); subplot(312); plot(c); 图3主要程序为[nc,nl] = upwlev(c,l,'db1'); subplot(313); plot(nc);
一维系数的直接小波重构	upcoef	Y = upcoef(O,X,wname,N)Y = upcoef(O,X,wname,N,L)Y = upcoef(O,X,Lo_R,Hi_R,N)Y = upcoef(O,X,Lo_R,Hi_R,N,L)Y = upcoef(O,X,wname)Y = upcoef(O,X,wname,1)Y = upcoef(O,X,Lo_R,Hi_R)Y = upcoef(O,X,Lo_R,Hi_R,1)	用来计算向量X(信号系数)向上N步的重构小波系数，N为正整数。O=a低频重构，O=d高频重构，L是对向量中间长度L进行重构。是一维小波分解系数的直接重构，它重建的是原信号在指定层次的高频或者低频分量。也就是说，这个信号不是原本的信号，而且某个层次上的逼近。
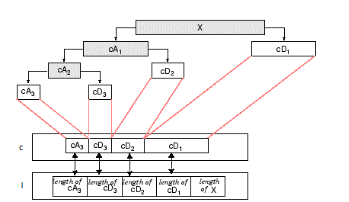
多尺度一维小波分解	wavedec	1. [C,L]=wavedec(X,N,'wname') 2. [C,L]=wavedec(X,nLo-D,Hi-D)	用于信号的多层分解的一维离散小波变换： 函数返回 N 层分解的各组分系数 C(连接在一个向量里)，向量 L 里返回的是各组分的长度。Lo_D (低通滤波器)、 Hi_D(高通滤波器) 对信号进行分解。分解的结构如下：
多尺度一维小波重构	waverec	1. X=waverec(C,L,'wavename')2. X=waverec(C,L,Lo_R,Hi_R)	X是重构信号；<