量子叠加态系数_斯坦福大学量子力学学习笔记——6.1叠加态和本征态

波的叠加

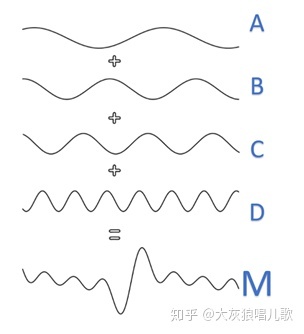
我们现在考虑一下下面的问题，有一个波M，见图1，我们要描述M的震动，但是M的振幅和频率都是随机的，很难用定量的语言去描述它的运动，那么我们现在可以把M波分解为A,B,C,D四个波的叠加，这样M的波动就很容易的被定量描述。

图1 波的叠加和分解

在量子力学中也是一样，我们在解薛定谔方程的时候求得了本征方程和本征函数，那么除了本征方程和本征波函数意外也存在着本征函数的叠加态，叠加态可以写成为本征态不同比例的叠加。那么这个和傅里叶中的频域展开是不是很像，如果真的是满足展开，那么不同本征值之间还需要正交。

图2 一维无限深势阱的本征解

傅里叶变换

我们复习一下，傅里叶频谱展开，对于f(t)函数，0<t<

，总是可以找到一组合适的

，将f(t)写成三角函数的展开，并且三角函数的频率是成倍增加：

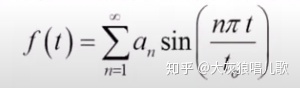
我们这里将不会对这个方程进行证明，但是我们需要掌握这种展开的概念，并且知道如何求解

。如果我们将变量t，变换为z，因此有函数f(z),0<z<

,于是我们可以把f(t)分解为：

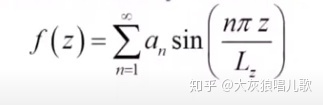
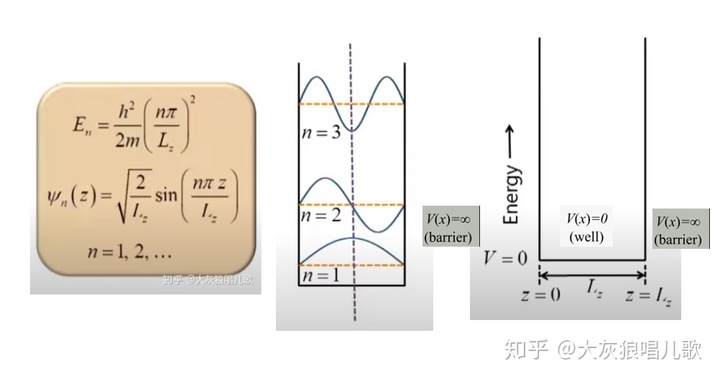
本征态和叠加态

我们求解了一维无限深势阱里面的本征函数为：

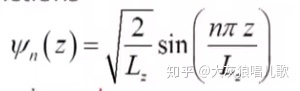
我们现在用

来代替三角函数在进行展开，那么系数也只是差了一个常数，因此有：

那么也就是在[0,

]的任意函数都可以写成

的叠加，只是前面的系数

不同。

函数的基矢（Basis sets of functions）

一系列像

这样用来函数，可以用来表示任意函数f(t),

叫做函数的基矢（basis set of functions）。一般我们简称为基矢（basis），展开的系数

叫做展开系数（expansion cofficients）。

总结

因此我们以后讨论波的时候，不在用在位置处的振幅，而是说这个函数=0.5个本征态1+0.2本征态3+0.3本征态2，或者其他例子。