最接近点对问题一维Java算法_最接近点对问题的算法分析

在二维平面上的n个点中，如何快速的找出最近的一对点，就是最近点对问题。

一种简单的想法是暴力枚举每两个点，记录最小距离，显然，时间复杂度为O(n^2)。

在这里介绍一种时间复杂度为O(nlognlogn)的算法。其实，这里用到了分治的思想。将所给平面上n个点的集合S分成两个子集S1和S2，每个子集中约有n/2个点。然后在每个子集中递归地求最接近的点对。在这里，一个关键的问题是如何实现分治法中的合并步骤，即由S1和S2的最接近点对，如何求得原集合S中的最接近点对。如果这两个点分别在S1和S2中，问题就变得复杂了。

为了使问题变得简单，首先考虑一维的情形。此时，S中的n个点退化为x轴上的n个实数x1，x2，...，xn。最接近点对即为这n个实数中相差最小的两个实数。显然可以先将点排好序，然后线性扫描就可以了。但我们为了便于推广到二维的情形，尝试用分治法解决这个问题。

假设我们用m点将S分为S1和S2两个集合，这样一来，对于所有的p(S1中的点)和q(S2中的点)，有p

递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2}，并设

d = min{ |p1-p2| , |q1-q2| }

由此易知，S中最接近点对或者是{p1,p2}，或者是{q1,q2}，或者是某个{q3,p3}，如下图所示。

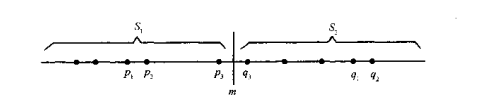
如果最接近点对是{q3,p3}，即|p3-q3|

此时，一维情形下的最近点对时间复杂度为O(nlogn)。

在二维情形下，类似的，利用分治法，但是难点在于如何实现线性的合并？