103. HIN(异构信息网络)
102. Hypergraph(超图):
- 一条边上有多个点的图
- 二阶超图: 平时使用的图
- 三阶超图:

101.hard sample mining:
- 取那些识别不好的样本再次进行模型微调
100.ground truth:
- 直述:有监督学习里的真值,有效值,标准值
90.范数:
- 范数主要是对矩阵和向量的一种描述,有了描述那么“大小就可以比较了”,从字面理解一种比较构成规范的数。有了统一的规范,就可以比较了。
- 例如:1比2小我们一目了然,可是(3,5,3)和(6,1,2)哪个大?不太好比吧
- 矩阵范数:描述矩阵引起变化的大小,AX=B,矩阵X变化了A个量级,然后成为了B。
- 向量范数:描述向量在空间中的大小。更一般地可以认为范数可以描述两个量之间的距离关系。
- L-0范数:用来统计向量中非零元素的个数。
- L-1范数:向量中所有元素的绝对值之和。可用于优化中去除没有取值的信息,又称稀疏规则算子。
- L-2范数:典型应用——欧式距离。可用于优化正则化项,避免过拟合。
- L-∞范数:计算向量中的最大值。
89.梯度裁剪:
- 直述:使得梯度不超过一个阈值
- 目的:解决梯度消失,梯度爆炸问题
- 公式:
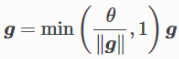
- 把所有梯度接成一个向量g
- 假设裁剪的阈值是
- 则,裁剪使得||g||不会超过
88.核范数:
- 矩阵奇异值的和,用于约束矩阵的低秩
- 对于稀疏性质的数据而言,其矩阵是低秩且会包含大量冗余信息
- 冗余信息可被用于恢复数据和提取特征
87.奇异值:
- 矩阵里的概念
- 一般通过奇异值分解定理求得
- 定义:设A为m*n阶矩阵,q=min(m,n), A*A的q个非负特征值的算数平方根,叫做A的奇异值
- 奇异值分解是线性代数和矩阵论中一种重要的矩阵分解法,适用于信号处理和统计学等领域
86.拉普拉斯矩阵:
- L=D-A: D----度矩阵,A----领接矩阵
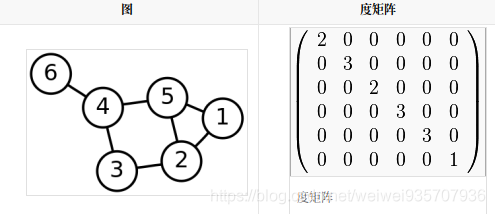
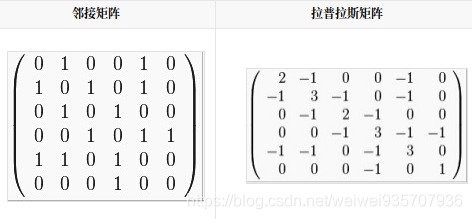
- 拉普拉斯矩阵是半正定矩阵
- 特征值中0出现的次数就是图连同区域的个数
- 最小特征值是0, 因为拉普拉斯矩阵每一行的和均为0
- 最小非零特征值是图的代数连通度
85.弱监督学习:
- 已知:数据和其一一对应的弱标签
- 目的:学习映射,将数据映射到更强的一组标签
- 解释:标签的强弱是指标签蕴含信息量的多少
- 例:已知图中有一只猪,学习住在哪,猪和背景的分界线
84.Benchmark
- 基准
83.Monocular Depth Estimation:单目深度估计
- 直述:从二维图像中,估计出三维空间
分割线:倒着来。。。。。。。。。。。。。。。
1.Memory:
- 我的出处:ECN。元学习时提及此方式。
- 原理:目标域的图片经网络题取出特征向量,存储到memory中;下一次新的即可和上次的做聚类;
- 公式:
(其中
是随着epoch不断线性增加的:
PS:但为什么新特征的影响会越来越大?)
- 用处:
- 1.Domain Adaptation,用新提取出的特征向量和旧的做聚类,可使模型在目标域上的泛化能力增强
- 2.因为是在整个训练过程中不断积累,所以能够很好地传递全局性质,不仅仅只在一个batch中。
2.Domain Adaptation:域适应
- 我的出处:ECN的主题。老师提及。语义分割也有此问题。
- 描述:用源域训练数据得到模型,在目标域上的泛化能力不强。
- 背景:常常出现在无监督和半监督学习。
3.Semantic Segmentation:语义分割
4.GCN:图卷积
- 我的出处:师兄提到过,CVPR19的工作中,不仅有可以做多标签识别,还有做半监督的,所以有必要~
- 背景:可以把图(邻阶矩阵)做输入,以探究信息训练模型
- 原理:
(1)输入:
1)特征矩阵 (节点数,每个结点的特征数)
2)邻阶矩阵A
(2) 隐藏层的传播规则: (
:非线性激活函数,W:权重矩阵,决定了下一层的特征数)
- (补)拉普拉斯矩阵:

1)
2)(GCN很多论文中用这种)
3)
- 相关名词:谱聚类,拉普拉斯矩阵,传播规则
5.Residual Network:残差网络(大名鼎鼎的ResNet)
- 我的出处:ECN修改预训练模型的时候,作者提及未懂。接下来时间又见到很多次。
- 背景:用深度网络比用浅层网络在训练集上的效果更差(不是过拟合:注意因为不是在测试集而是在训练集上)
- 作用:解决网络退化问题。即又保持了深的网络的高准确度,又避免了它会退化的问题。
- 实现:shortcut(identity mapping)
(其实很简单:每一层不仅取决于上一层,还要取决于很久之前的层)

- 存在的问题:如果





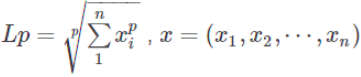
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2428
2428










