这节课我们主要思考的问题是提升DQN得一些小tips,其中第一个就是double DQN。
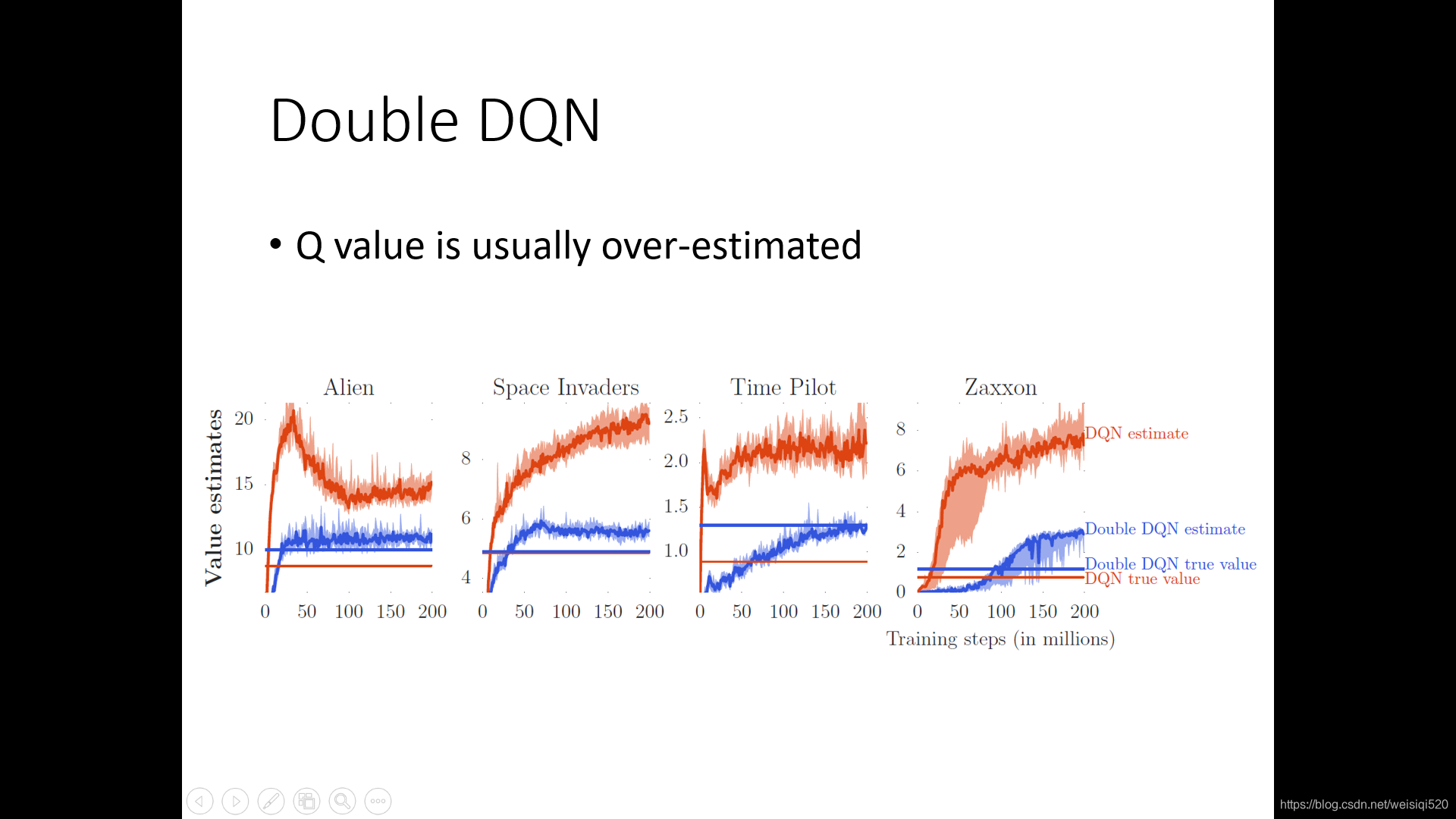
其中红色锯齿状得线就是使用最初的DQN所得到得Q估计得值,之后红色的直线是DQN算法所得到的真实的Q值。蓝色锯齿状线是使用double DQN所得到的Q估计值,蓝色直线是double DQN算法得到的真实的Q值。
我们可以看到使用DQN得到的Q估计都是比较大的,这就是我们所说的DQN往往会高估。红色锯齿状的线往往会上升,是因为q值往往是和策略相对应的,越来越高就意味着策略会越来越好。
蓝色锯齿线往往比红色的低很多,同时蓝色锯齿线往往和蓝色的直线比较接近,这意味着double DQN不会过分的高估自己的Q值。

我们先来研究一下为什么使用DQN的时候Q值总是容易被高估。我们使用DQN的时候总是会让左边的Q估计和右边的Q现实越来越接近,但是Q现实总是倾向于选高。因为任意一个Q(s.a)如果高估了,都会导致整个的Q现实变高。所以使用DQN的时候很容易导致所求的Q估计会过高。

下面我们来讨论一下如何使用double DQN来解决这些问题。原始的DQN中计算Q现实的时候都是直接选择最大的下一步Q值,之后直接加进去的,我们使用double DQN的时候一般都是选择两个Q,将计算value的Q值和选择action的Q值分开。Q是用来选择action的,之后Q’是用来计算value的。先用一个Q来选择最大的action,之后使用Q’来计算这个value。将两个Q的算式作为Q现实
打个比方,就是Q相当于是一个提案的人,之后Q’相当于是一个最终选择的人。当Q被估计大的时候,最终计算value的Q’没有高估就会计算出一个比较正常的值。同样当Q’高估了一个a的值的时候,只要Q没有选择这个a,就没差。
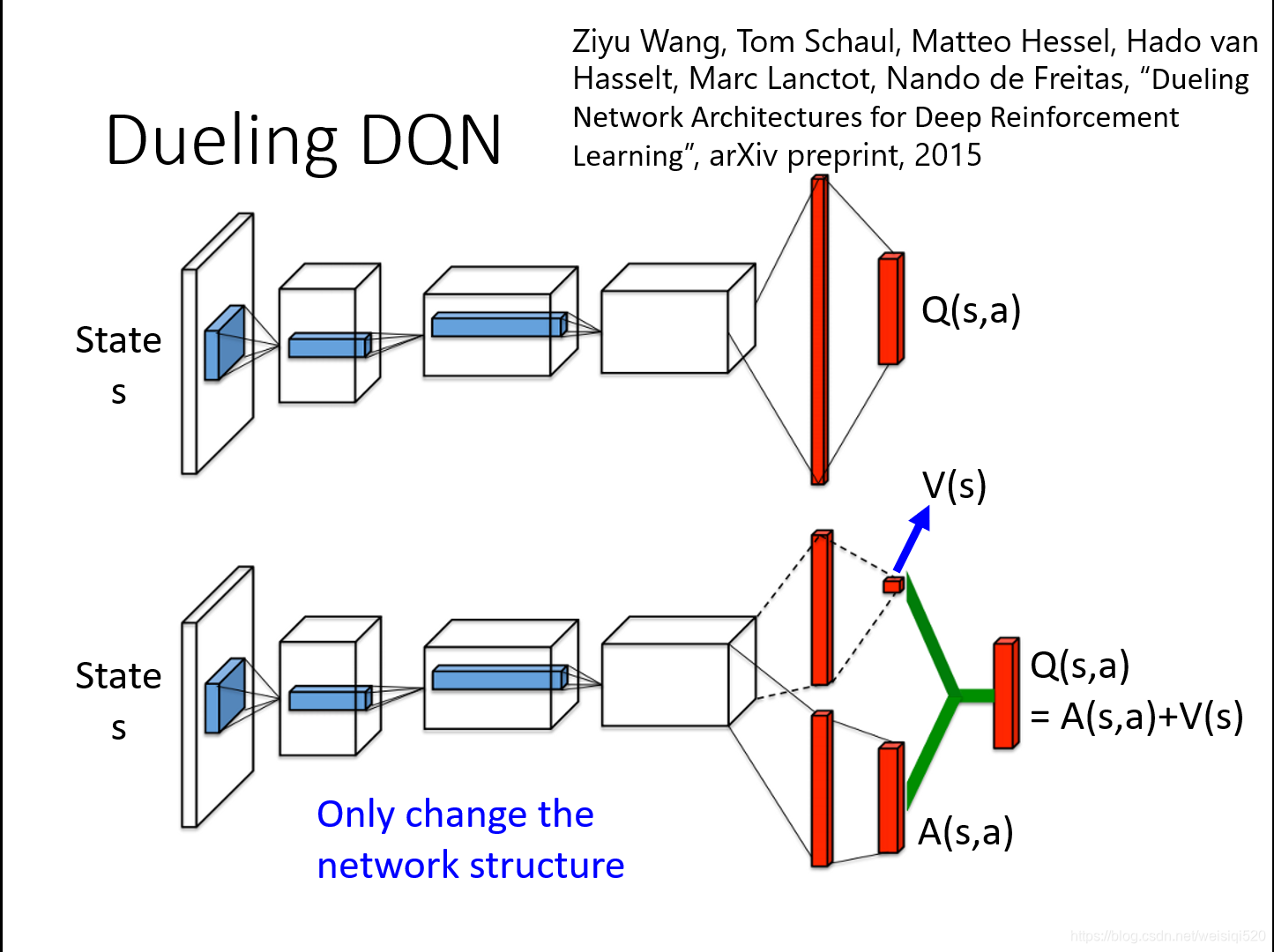
Dueling DQN和DQN的区别就在于前者是改变了network的架构。
之前就是输出一个Q(s,a)的值,但是Dueling DQN做出了改变:他是输出两个值,其一是一个标量V(s),其二是一个向量A(s,a)。举个例子就是算出的V(s)(这个状态s的价值)是1,之后Q(s,a)(在状态s的时候,每一个可以选择的a的值)假设其中有三个可以选择的a1,a2,a3,其中Q(s,a1)是2,A(s,a2)是0,A(s,a3)是-2,那么我们要做的就是将标量加入到向量的每一项,作为最后的Q值,所以Q(s,a1)是3,Q(s,a2)是1,Q(s,a3)是-1。
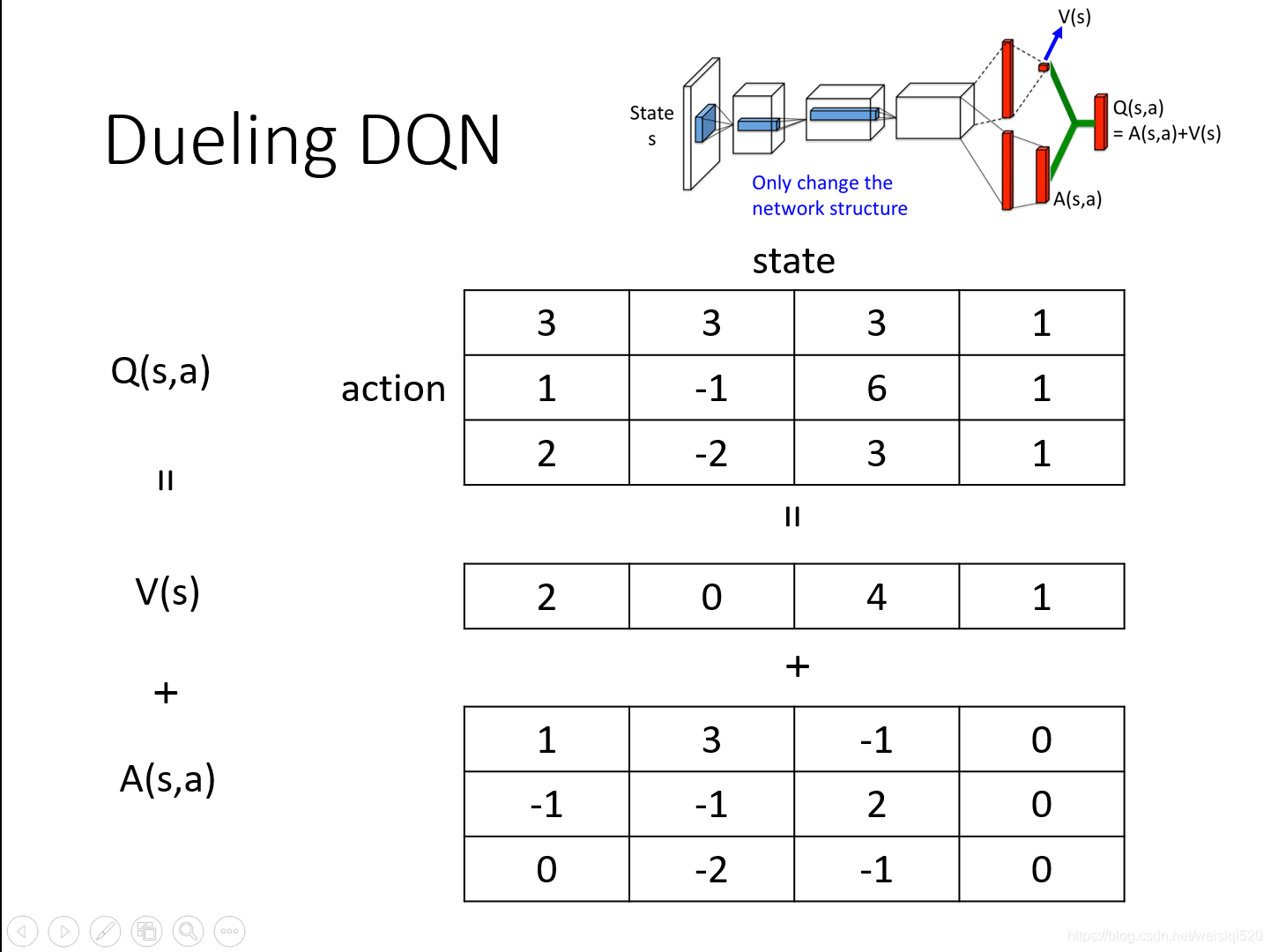
举个例子其实就是将V的值加入到A的每一项中,之后得到的就是Q的值。
其实使用Dueling DQN之后就是如果想更新Q的话,我们只要更新一个V就好啦!这样就会比较有效率。更改的时候效率会比较高。
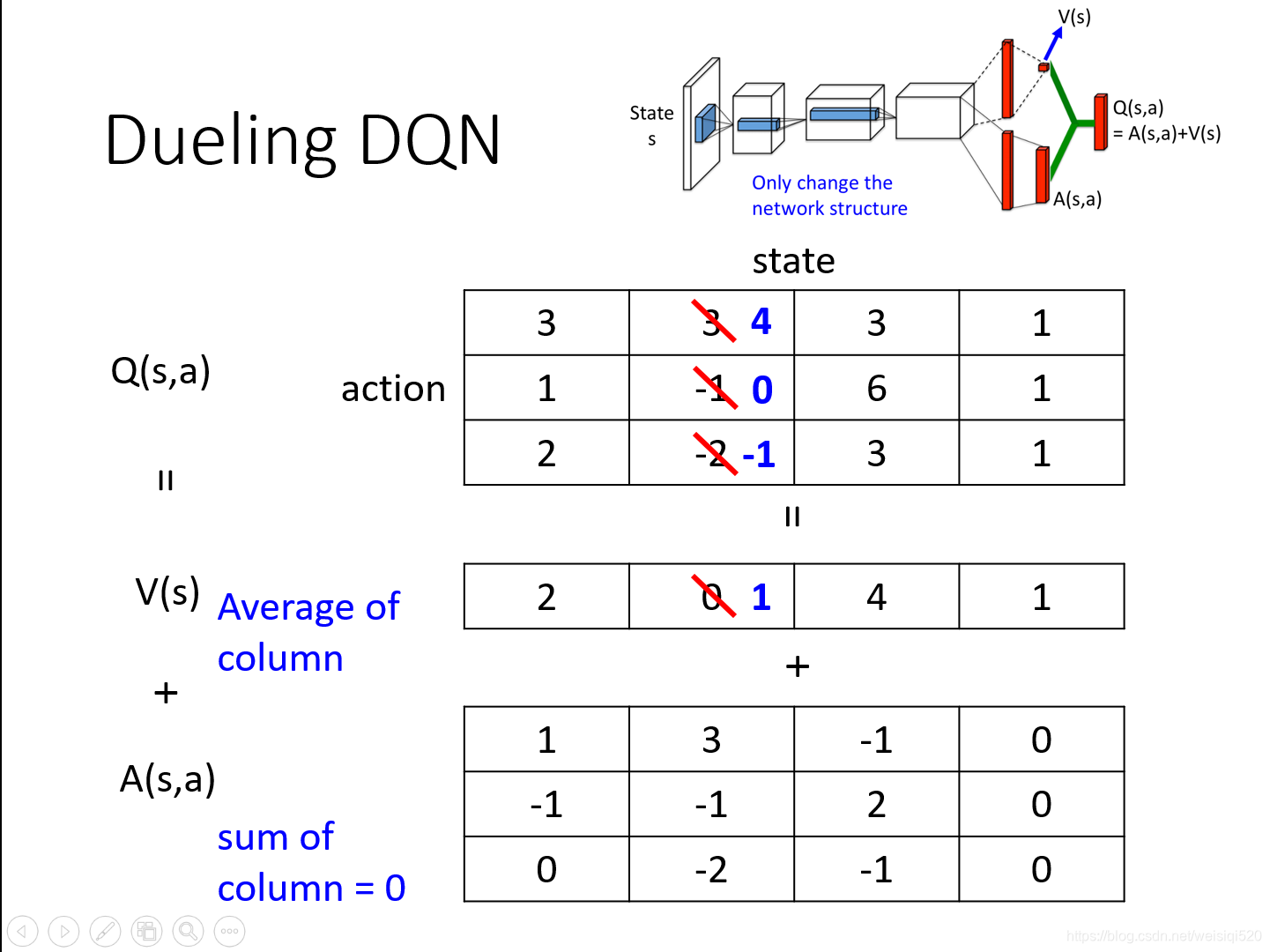
就是说如果想更新第二列的3,-1使其变成4,0的话,我们可以直接将V更新为1,这样-2就变成了-1。这样在更新很小的代价下,完成了Q的更新,十分的有效率。
同时有一些小的策略,就是让V为Q的均值,让A每一项相加为0。
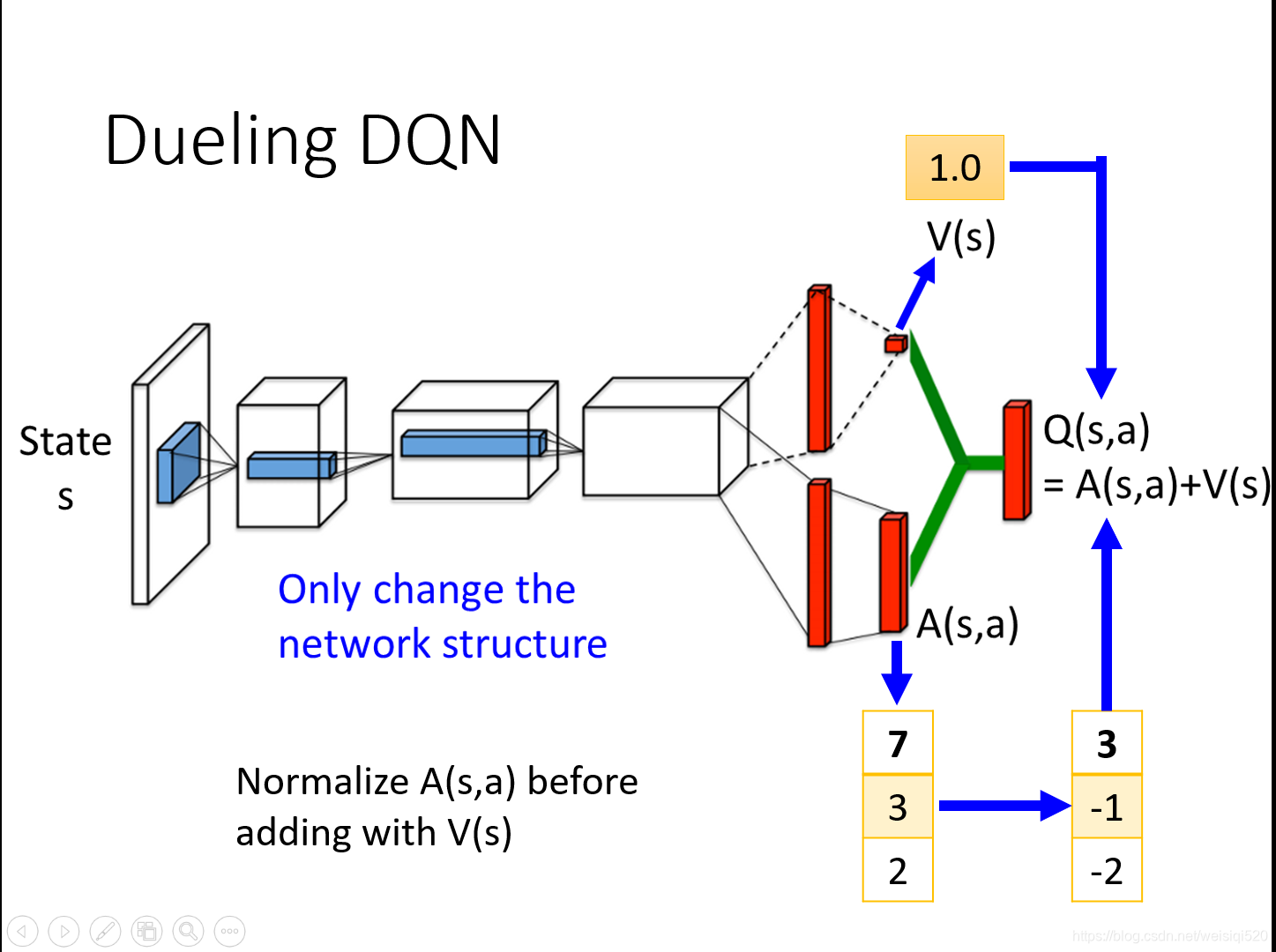
这里原来的值是7,3,2,我们先算一下这里的均值是4。之后用A中的每一个都减去4,得到3,-1,-2。最后加上1,得到最后的Q值。
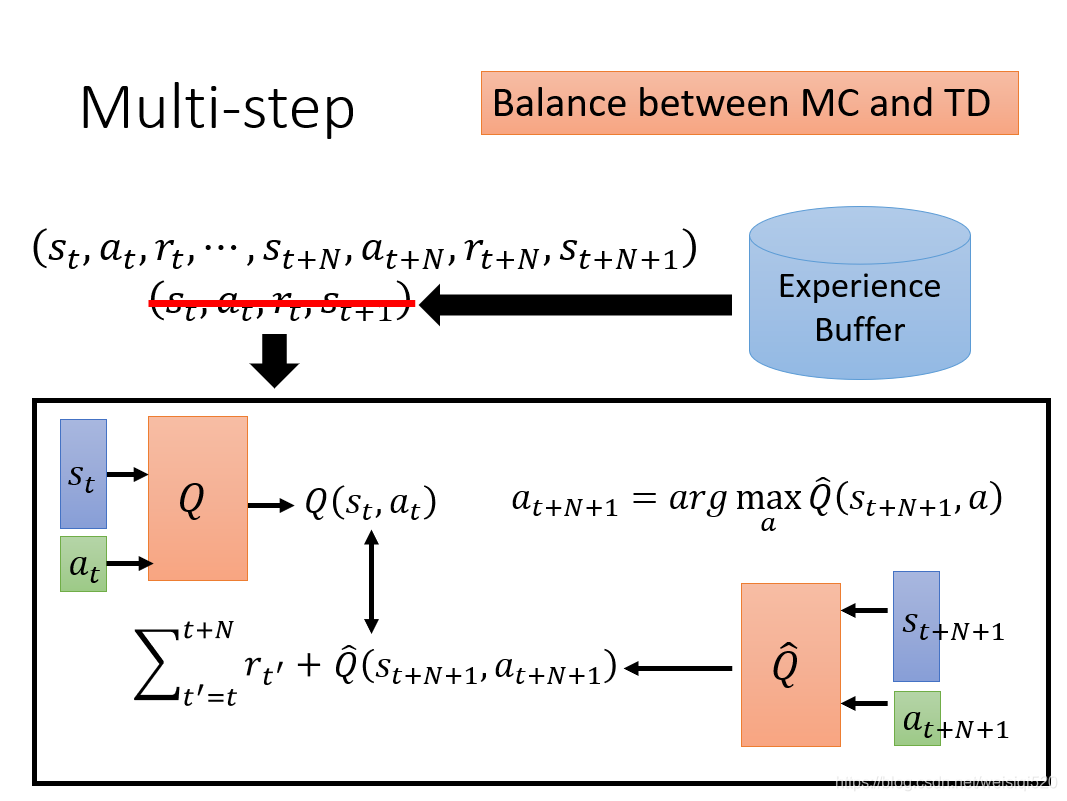
下一个tip就是将MC算法和TD算法做一个简单的结合。之前我们预测Q或者V的时候我们使用了MC算法或者TD算法。MC是回合更新,就是一个马尔可夫链全部走完才进行更新,而TD是单步更新,也就是走一步一更新。MC更加准确,但是方差很大,不稳定,TD方差小,比较稳定,但是却不如MC准确。我们想能不能将两种算法进行一个结合呢!
于是就有了Multi-step的方法产生,就是我们不更新一步,我们更新n步。但是具体更新几步(n的具体数值)是一个超参数,需要进行实验来调整一下。

下一个tip是Noisy Net,这一步的作用是提高探索性。我们最初为了探索性而采用的方法是Epsilon Greedy,但是使用这种方法,造成的探索性是不稳定的,就是这次可能会采用这个a,下一次不一定采用什么a,这就造成了一种不确定性,不利于训练。
使用Noisy Net,就是在Q-function的最初参数上加入一个噪声,并且这个噪声在这次训练中是固定不变的。这样的结果就是这个eposide遇到状态s选择的a和下一次遇到s时候选择的a是同样的。但是在之后的eposide所表现出来的不确定性又是不同的。

当把不确定性放在action的时候(使用Epsilon Greedy)时候,当遇到相同的s的时候选择的a可能是不同的,这就是一个完全随机的policy策略,这种完全随机的策略就像是毫无章法的尝试一样,是很难得到最终结果的。
但是把不确定性放在参数中(使用Noisy Net )时候,当遇到相同的s的时候选择的a是完全相同的,就是一个有规律的policy策略,每一次改变参数中的噪声,就相当于是改变了这次的policy,这是一种有章法的尝试,比较有效。
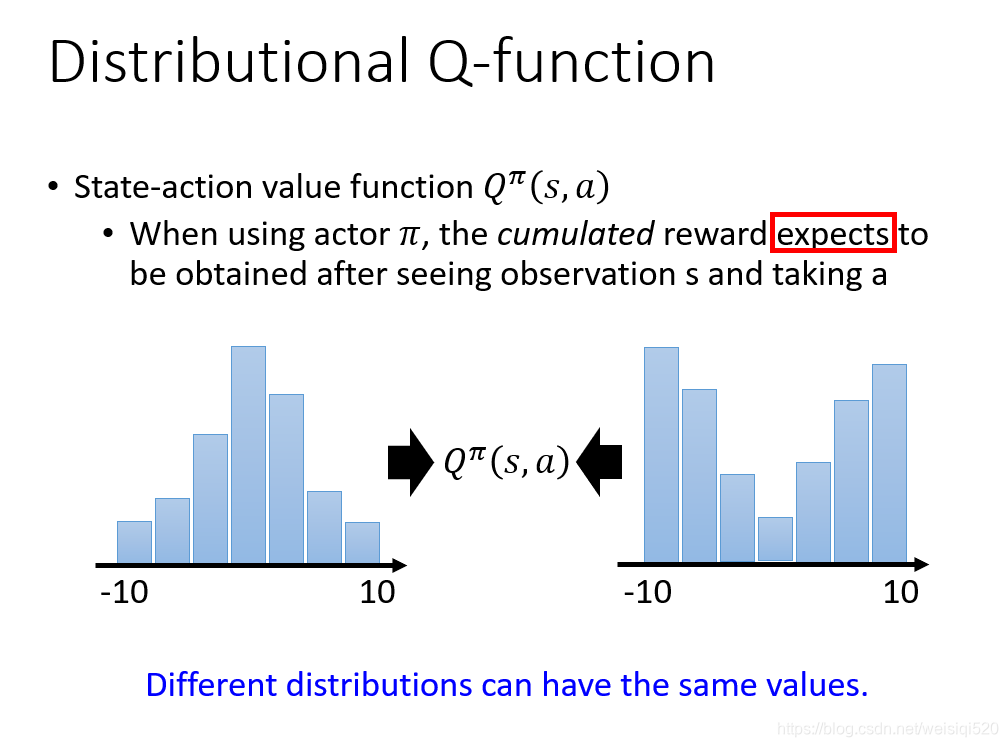
下一个tip是Distributional Q-function,Q其实是一个均值是Distribution的一个均值,他不是一个单独的值,而是一个分布,之后对分布求均值之后的结果,这样造成的结果就是有时候即使是分布的不同,但是最后的结果q却有可能是相同的,这就容易造成混淆。
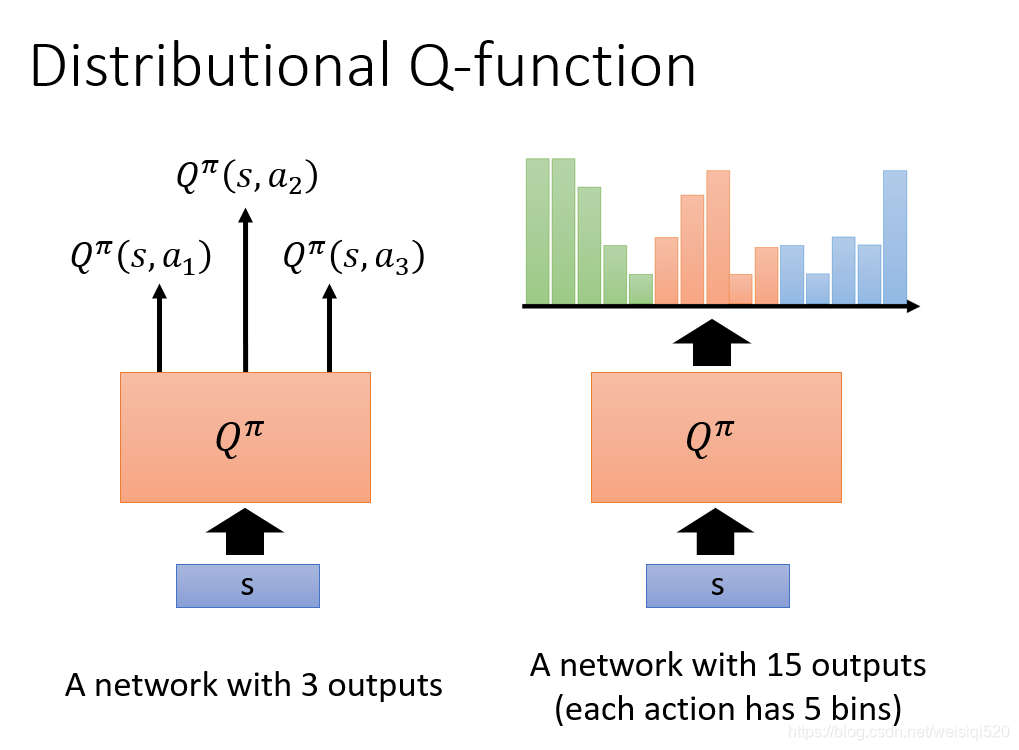
在这个例子中,a1,a2,a3的q值对应的分布用右边绿色,橘色,蓝色表示。我们求得不再是q值,而是对应的分布Distribution。这样的方法会让计算更加的稳定有效。
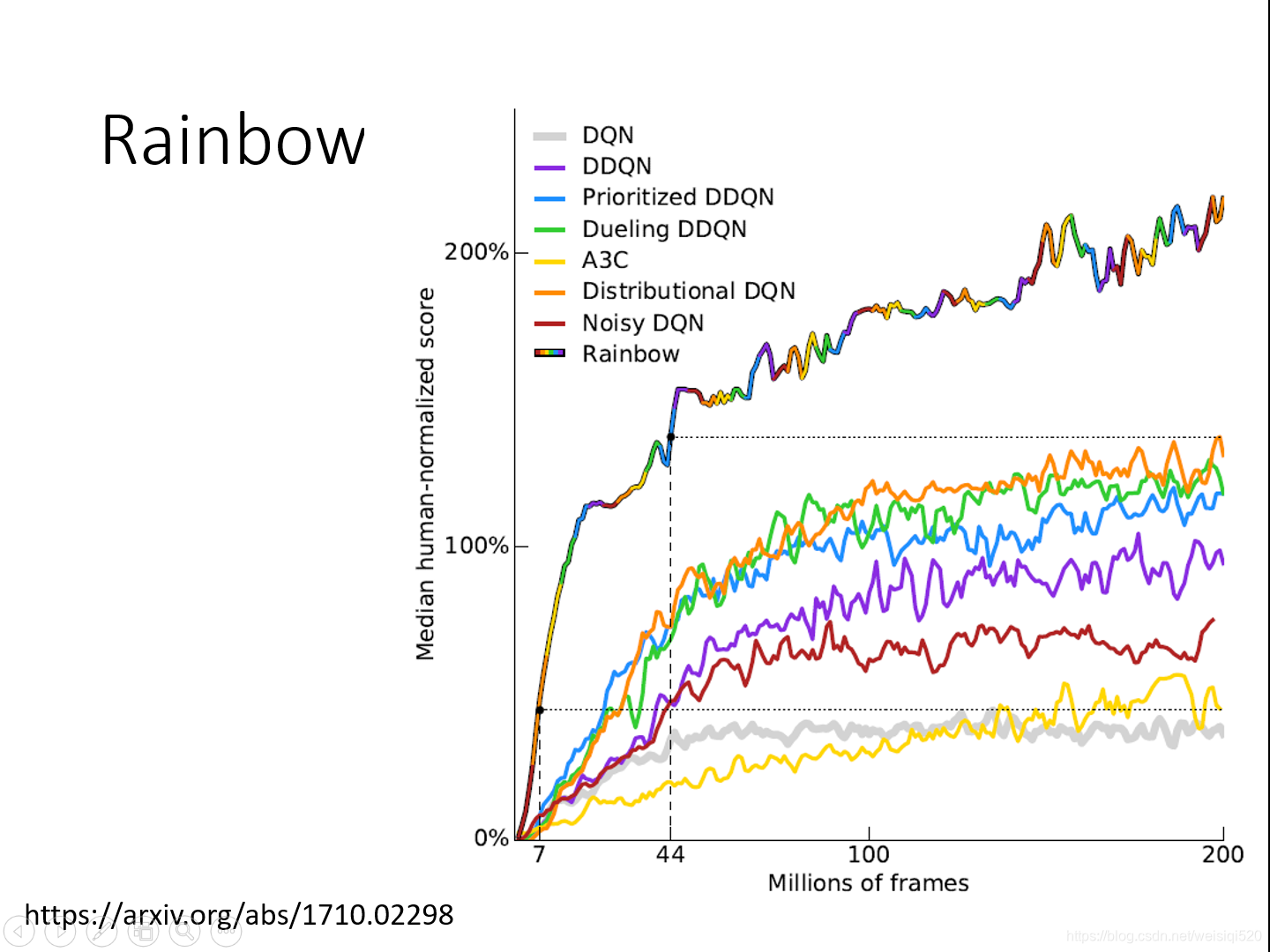
下一个tip就是rainbow,这种方法其实就是将所有的强化学习方法放到一起使用,哪个方法在那一段是好的,最后在那一段就用表现好的那个方法,这样就会有一个最好的方法。
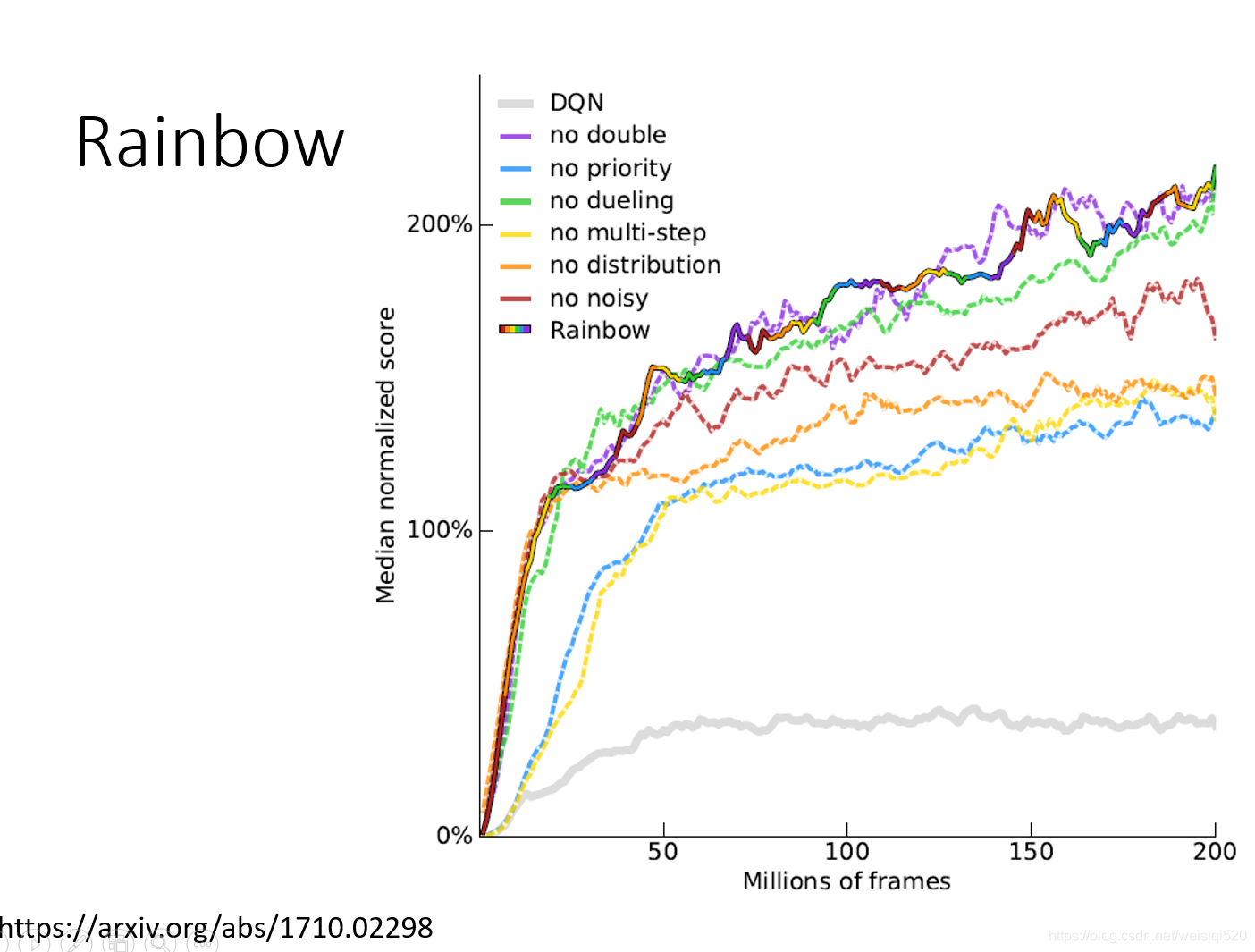





 本文介绍提升DQN的小技巧,包括double DQN可避免Q值高估,Dueling DQN改变网络架构提高更新效率,结合MC与TD算法的Multi - step方法,Noisy Net提高探索性,Distributional Q - function让计算更稳定,rainbow综合多种强化学习方法。
本文介绍提升DQN的小技巧,包括double DQN可避免Q值高估,Dueling DQN改变网络架构提高更新效率,结合MC与TD算法的Multi - step方法,Noisy Net提高探索性,Distributional Q - function让计算更稳定,rainbow综合多种强化学习方法。
















 637
637

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








