机器学习-2

2018年8月2日 吴恩达机器学习4-6章

主要内容：多变量的线性回归(linear regression with multiple variables)；几个技巧让梯度下降算法(gradient descent)收敛的更快些；另一种minimize J(θ)的方法: normal equation；有关octave的操作；向量化(vectorization)；logistic regression: classification分类；

 

1、linear regression with multiple variables

multiple features:  n: 特征数

: value of feature j in ith training example; 第i个training example 中的第j个特征

hypothesis:   ;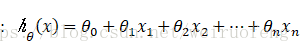

                        ;

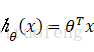cost function: 和单变量的形式一致

将梯度算法用于多变量线性回归模型中；

 

2、几种技巧让梯度下降算法收敛快些

(1) Feature scaling 将特征的取值进行缩放

(2) Mean normalization: replace xj with xj - μj to make features have approximately zero mean

xj = （xj - μj）/sj

(3) Learning rate

α太小：收敛速度过慢

α太大：不一定每一次迭代都会使cost function 减小；不一定收敛

 

3、标准方程法

;

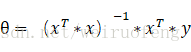design X: 将第i次training example中的所有特征值组成一个列向量；转置后作为X的第i行。

 

4、octave的操作

遇到不知道的操作：help 操作

 

5、向量化

可以得到高效的线性回归算法；用以替代for循环

 

6、logistic regression

classification

hypothesis:  利用logistic function组成hypothesis；

cost function: 不用之前线性回归模型中的square error function构建损失函数（根据这个得到的损失函数为非凸函数），利用                cost() =-y*log()-(1-y)*log()构建。

将梯度算法用到Logistics regression 所得形式和线性回归算法一致，但由于hypothesis不一样，所以算法完全不同。