数据安全系列8：数字签名

最新推荐文章于 2025-12-18 17:00:31 发布

原创最新推荐文章于 2025-12-18 17:00:31 发布 · 850 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#算法

算法专栏收录该内容

10 篇文章

订阅专栏

传送门

数据安全系列1：开篇

数据安全系列2：单向散列函数概念

数据安全系列3：密码技术概述

数据安全系列4：密码技术的应用-接口调用的身份识别

数据安全系列5：常用的对称算法浅析

数据安全系列6：从SM4国密算法谈到Bouncy Castle

数据安全系列7：常用的非对称算法浅析

什么是数字签名

关于数字签名，可以通过官方的定义：

签名算法是指数字签名的算法。数字签名，就是只有信息的发送者才能产生的别人无法伪造的一段数字串，这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。数字签名是通过一个单向函数，对要传送的信息进行处理得到的用以认证信息来源，并核实信息在传送过程中是否发生变化的一个字母数字串。应用最为广泛的三种签名算法是：Rabin签名、DSS签名、RSA签名。

数字签名要解决的问题

在前面用了3节来讨论数据安全的一个非常重要核心应用分支：加密。内容包括了：

对称、非对称算法
JAVA领域的标准加密体系基础架构JCA框架、JCE扩展实现
常见的算法及其实现
JAVA中使用最广泛的三方包BouncyCastle

除此以外，在数据安全中还有一块非常重要的核心应用分支：认证。这部分又包括典型的3个场景：

防止篡改保证完整性的单向散列函数
防止伪装的认证技术消息认证码
防止抵赖的不可否认技术数字签名

这也就是在数据安全系列3：密码技术概述提到的信息安全面临的几个主要问题：

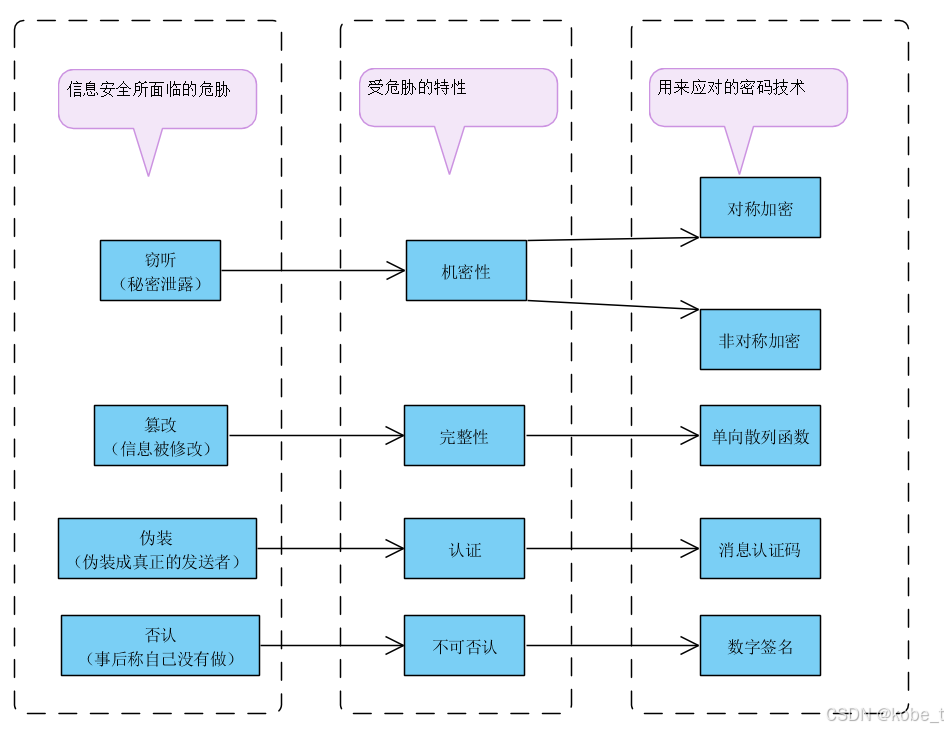
单向散列函数在数据安全系列2：单向散列函数概念里面有过单独的讨论；消息认证码在数据安全系列4：密码技术的应用-接口调用的身份识别里面通过应用间身份认证调用API例子来简单讨论过；而数字签名可以通过非对称算法来实现，所以这里正好接着非对称算法的讨论来整体看看数字签名技术！

消息认证码的局限性

关于消息认证码没有单独讨论过，只是在前面提到过。因为消息认证码不是这一节的重点，这里只是简单讨论下，还是回顾一下以前的一张图：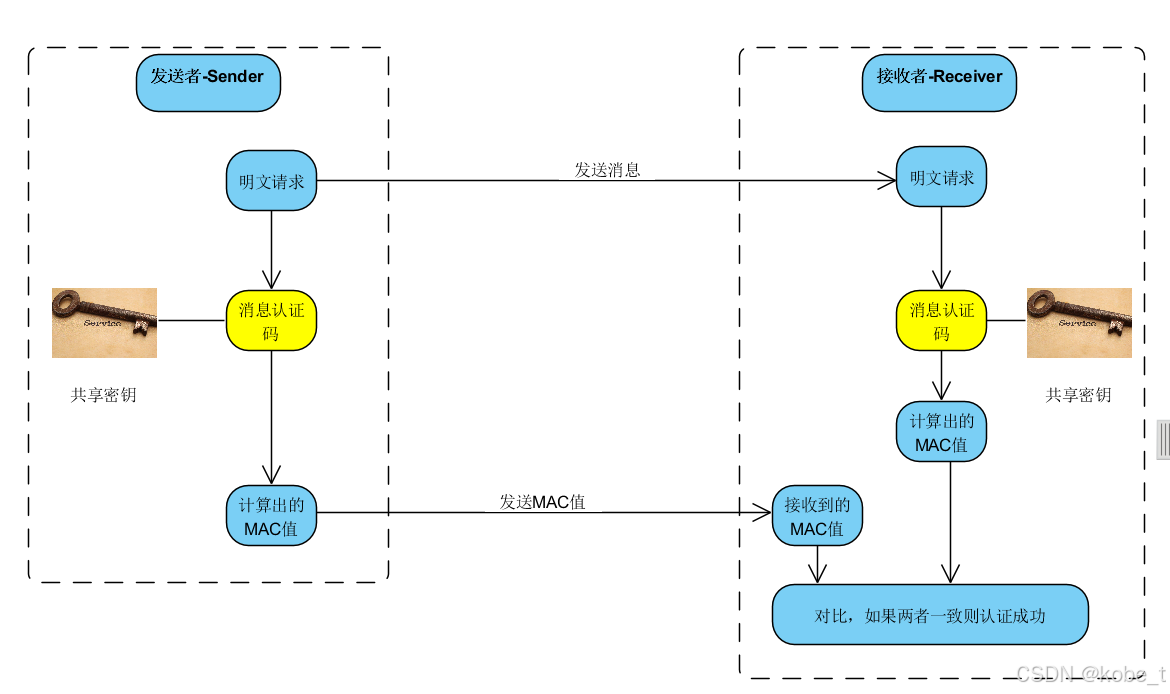

在这样的交互过程中，交互的双方需要共享密钥，也即是前面的对称密钥
要计算MAC值，必须持有共享密钥，没有就无法计算MAC值，消息认证码正是利用此特性来完成所谓的认证的。

其实共享密钥在软件开发中还是是很常见的，不仅是在内网的服务间调用，甚至一些开放平台的使用的Oauth2协议也是会涉及：

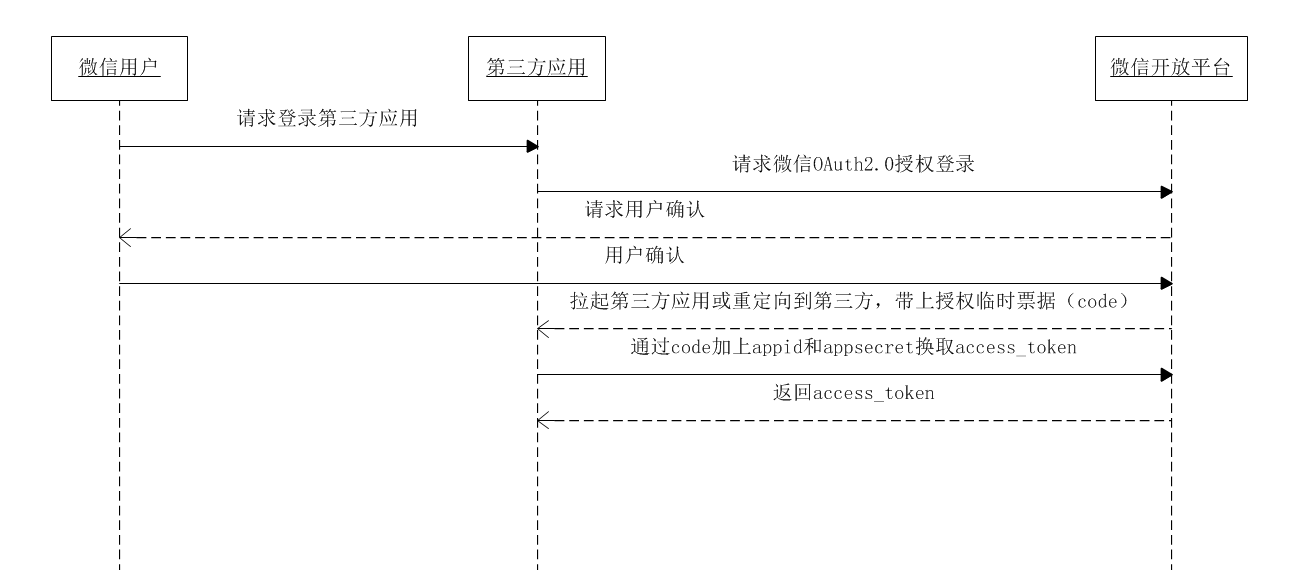
这里的appsecret就是微信开发平台、第三方应用共享的，这样就可以保证其它人（这里代指应用）在不知道appsecret的情况下是无法通过微信开发平台的验证。不过世界上没有完美的方案，问题出就出在共享上：

第三方证明
防止否认

下面通过一个模拟例子来看看，Hmac在实际场景中可能会出现的问题。

场景：在线支付系统

假设有一个简单的支付系统，Alice和Bob都共享同一个密钥K（注意现实情况中肯定不会这么设计，这里仅做演示说明。这里的Bob其实也最可能是各种发卡机构，比如银行、支付宝等，不会是商家，它们才管理着用户的密码）。

支付流程：

Alice向Bob的商家账户支付100元
系统需要生成一个支付凭证，使用HMAC-SHA256进行验证

消息结构：

支付方: Alice
收款方: Bob  
金额: 100元
时间戳: 2024-01-01 12:00:00

生成HMAC：

import hmac
import hashlib

key = b"shared_secret_key_123"
message = b"Alice|Bob|100|2024-01-01 12:00:00"
hmac_digest = hmac.new(key, message, hashlib.sha256).hexdigest()
# 结果: a1b2c3d4e5f6...

问题出现：

几天后，Alice否认了这笔支付：

Alice的抵赖理由：

"我没发起这笔支付"
"可能是Bob自己生成的，因为他也有共享密钥"
"系统可能被黑了，密钥泄露了"

Bob的困境：

Bob无法向第三方（如仲裁机构）证明这笔支付确实来自Alice，因为：

密钥是共享的：Bob也知道密钥，可以自己生成任何消息的合法HMAC
无法确定消息来源：相同的HMAC可以由任何知道密钥的人生成
没有身份绑定：HMAC不包含Alice独有的身份标识（如私钥）

而这个问题在数字签名技术面前得到了解决！

数字签名的不同之处

要使用数字签名就要利用前面说的非对称算法，也就是公钥密码。在用公钥密码加解密时：

非对称算法从这一点入手，彻底避免了密钥共享的问题：分离加密密钥与解密密钥，加密密钥称为公钥，解密密钥称为私钥。公钥（Public Key）可以被公共，私钥（Private Key）不被并公开。只要拥有加密密钥，任何人都可以进行加密，但没有解密密钥是无法解密的。这样就意味着公钥不仅能被公开也能被共享，只有拥有解密密钥的人才能解密

使用方式一句话总结：公钥加密，私钥解密！而用公钥密码来进行签名时，情况与此相反：

私钥加签，公钥验签！看来就像加密的"反过来"用：

常用的数字签名方法

既然是用公钥密码来实现数字签名，正好RSA、SM2是比较常用的非对称算法，就来看代码层面怎么实现的吧。

RSA

生成签名

/**
     * 使用RSA私钥对数据进行签名
     */
    public static String sign(String data, PrivateKey privateKey) throws Exception {
        // 使用SHA256withRSA算法
        Signature signature = Signature.getInstance("SHA256withRSA");
        // 初始化签名对象
        signature.initSign(privateKey);
        // 更新数据
        signature.update(data.getBytes());
        // 生成签名
        return Base64.getEncoder().encodeToString(signature.sign());
    }

验证签名

/**
     * 使用RSA公钥验证签名
     */
    public static boolean verify(String data, String signatureStr, PublicKey publicKey) throws Exception {
        // 使用SHA256withRSA算法
        Signature signature = Signature.getInstance("SHA256withRSA");
        // 初始化验证对象
        signature.initVerify(publicKey);
        // 更新数据
        signature.update(data.getBytes());
        // 验证签名
        return signature.verify(Base64.getDecoder().decode(signatureStr));
    }

结合上一节的密钥生成，运行一下测试用例代码：

public static void main(String[] args) {
        try {
            
            // 测试加签、验签
            System.out.println("\n=== RSA 签名与验证示例 ===");
            KeyPair rsaKeyPair = RsaUtil.generateRsaKeyPair(2048);
            String dataToSign = "This is some data to sign.";
            String signature = RsaSignUtil.sign(dataToSign, rsaKeyPair.getPrivate());
            System.out.println("签名 (Base64): " + signature);

            boolean isVerified = RsaSignUtil.verify(dataToSign, signature, rsaKeyPair.getPublic());
            System.out.println("签名验证结果: " + isVerified);

        } catch (Exception e) {
            e.printStackTrace();
        }
    }

输出结果格式（因为生成的密钥会不一样，输出会不一样）：

=== RSA 签名与验证示例 ===
签名 (Base64): i87X5ElAUo50LUKobF1pB9jcAONiP7m9RJyMt8t+wRSTvDPMVvnb1eLNBWV6DWAdFi5Mdnrs3WWzyiXCRKLKB5ms+EKJkPH21/wk6KRxgyx9I0kFcudqc63XoTIvNI7rgqfdS2P9lXj/Pzh12ID6PDPsYzVWHaF6O5wIpW7EHatFl/3TPVpPdeFr1r1qSRrWdoP6/eXLV6OeWxiGdPLTtgkgTYcl6LSSQ2+BZ5idxDHeVdadERQg4Jy4AGWd6nrmugHdUabmR3cT8e3O+deZELmfBwDD5h7KP3U4q9djO8zY0X7Gq8GbKuC+ZoM0P5CLTencQHs9DoFr6imqM64Yng==
签名验证结果: true

签名的效率

在使用RSA进行数字签名的时候，指定了一个算法"SHA256withRSA"。那它具体是什么意思呢？在回答这个问题之前先来回顾上面提到的数字签名的用法：私钥加签，公钥验签！看来就像加密的"反过来"用。这里的"反过来"其实就是指数字签名的时候，使用私钥对待加密数据进行加密！

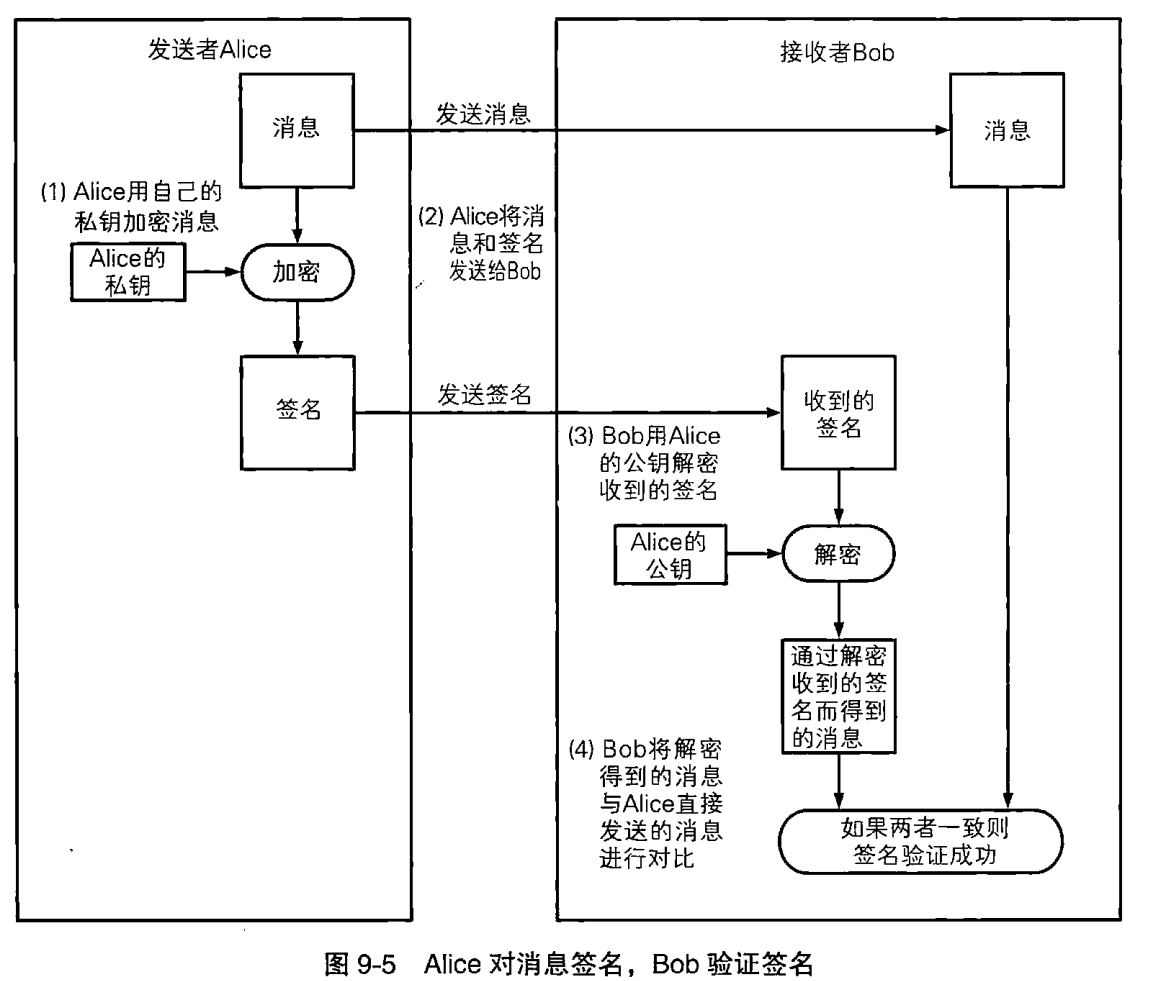
Alice用自己的私钥对消息进行加密
Alice将消息和签名发送给Bob
Bob用Alice的公钥对收到的签名进行解密
Bob将签名解密后得到的消息与Alice直接发送的消息进行对比

如果两者一致，则签名验证成功；如果两者不一致，则签名验证失败。

这个过程理论可行，实际上也是可行的。但问题在于，非对称算法的效率不够高甚至可以说是非常慢！所以这种直接对整个消息进行签名的方案在实际使用上并不可行。反之采用的是对消息的散列值进行签名的方法：

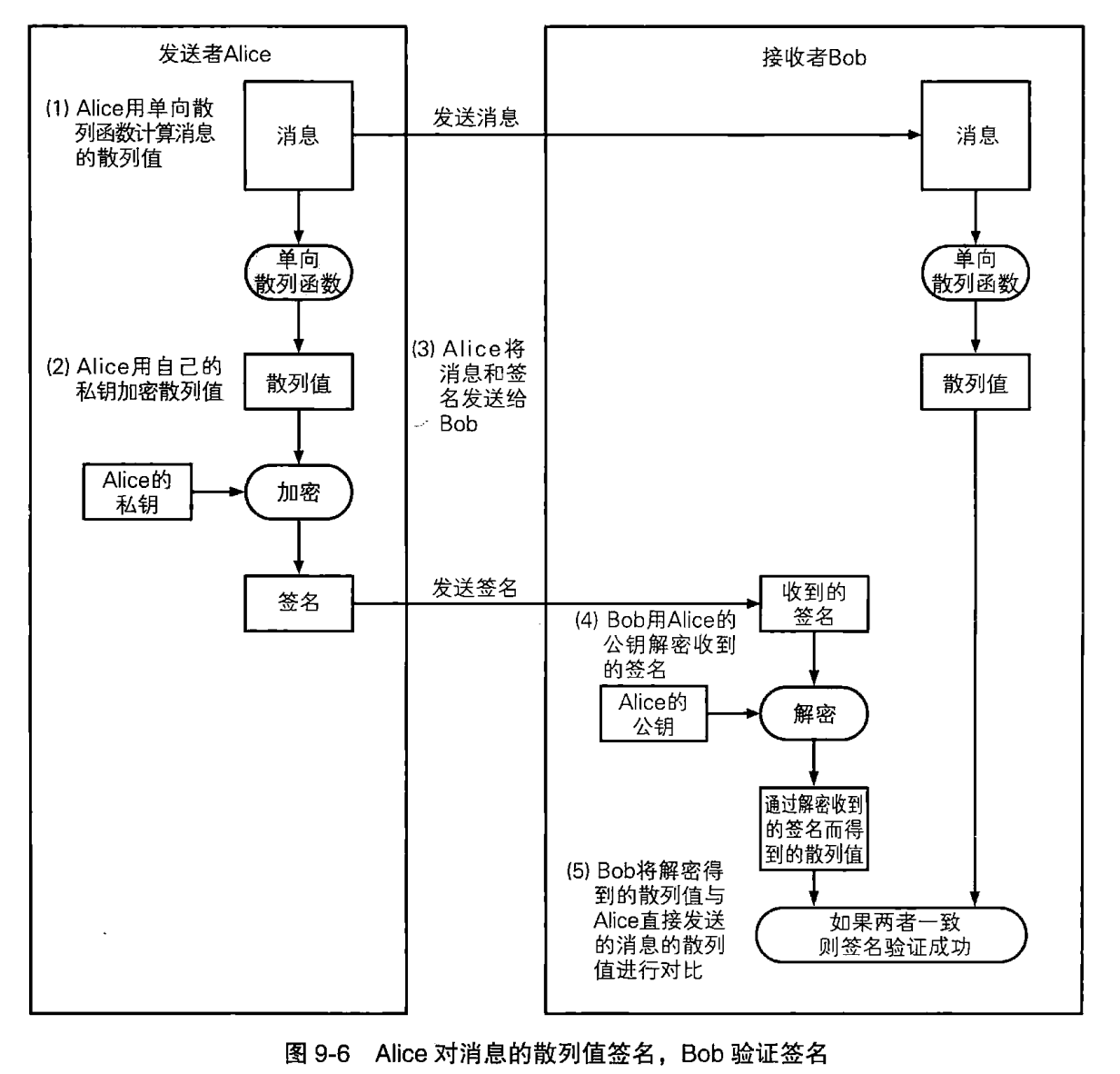
Alice用单向散列函数计算消息的散列值
Alice用自己的私钥对散列值进行加密
Alice将消息和签名发送给 Bob
Bob用Alice的公钥对收到的签名进行解密
Bob将签名解密后得到的散列值与Alice直接发送的消息的散列值进行对比

如果两者一致，则签名验证成功;如果两者不一致，则签名验证失败。

至此再回头看"SHA256withRSA"就不难理解了，SHA256指的正是哈希散列算法，而withRSA就是真正的使用RSA来进行签名。所以经典的SHA1withRSA、SHA384withRSA皆是同理。

SM2

生成签名

private static final ECDomainParameters DOMAIN_PARAMS;
    
    static {
        SM2_CURVE_PARAMS = ECNamedCurveTable.getParameterSpec(SM2_CURVE_NAME);
        DOMAIN_PARAMS = new ECDomainParameters(
                SM2_CURVE_PARAMS.getCurve(),
                SM2_CURVE_PARAMS.getG(),
                SM2_CURVE_PARAMS.getN(),
                SM2_CURVE_PARAMS.getH()
        );
    }

    public static ECDomainParameters getDomainParams() {
        return DOMAIN_PARAMS;
    } 

/**
     * SM2 签名
     */
    public static byte[] sign(PrivateKey privateKey, byte[] data) throws CryptoException {
        return sign((BCECPrivateKey) privateKey, data);
    }
    
    public static byte[] sign(BCECPrivateKey privateKey, byte[] data) throws CryptoException {
        ECPrivateKeyParameters privateKeyParams = new ECPrivateKeyParameters(
                privateKey.getD(), SM2Util.getDomainParams());
        
        SM2Signer signer = new SM2Signer();
        signer.init(true, privateKeyParams);
        signer.update(data, 0, data.length);
        return signer.generateSignature();
    }

验证签名

/**
     * SM2 验签
     */
    public static boolean verify(PublicKey publicKey, byte[] data, byte[] signature) {
        return verify((BCECPublicKey) publicKey, data, signature);
    }
    
    public static boolean verify(BCECPublicKey publicKey, byte[] data, byte[] signature) {
        ECPublicKeyParameters publicKeyParams = new ECPublicKeyParameters(
                publicKey.getQ(), SM2Util.getDomainParams());
        
        SM2Signer signer = new SM2Signer();
        signer.init(false, publicKeyParams);
        signer.update(data, 0, data.length);
        return signer.verifySignature(signature);
    }

结合上一节的密钥生成，运行一下测试用例代码：

public static void main(String[] args) {
        try {
            System.out.println("=== SM2 国密算法完整示例 ===\n");

            // 1. 生成密钥对
            System.out.println("1. 生成SM2密钥对...");
            KeyPair keyPair = SM2Util.generateKeyPair();
            PublicKey publicKey = keyPair.getPublic();
            PrivateKey privateKey = keyPair.getPrivate();


            // 2. 测试数据
            String originalText = "Hello, 国密SM2算法！这是一段测试文本。";
            byte[] data = originalText.getBytes("UTF-8");
            System.out.println("2. 测试数据:");
            System.out.println("   原文: " + originalText);
            System.out.println("   数据长度: " + data.length + " 字节\n");

            // 6. 签名验签测试
            System.out.println("6. 签名验签测试...");
            byte[] signature = SM2SignUtil.sign(privateKey, data);
            System.out.println("   签名: " + Base64.getEncoder().encodeToString(signature));
            boolean verifyResult = SM2SignUtil.verify(publicKey, data, signature);

            System.out.println("   签名长度: " + signature.length + " 字节");
            System.out.println("   验签结果: " + verifyResult + "\n");

        } catch (Exception e) {
            System.err.println("执行过程中发生错误: " + e.getMessage());
            e.printStackTrace();
        }
    }

输出结果格式（因为生成的密钥会不一样，输出会不一样）：

2. 测试数据:
原文: Hello, 国密SM2算法！这是一段测试文本。
数据长度: 52 字节

6. 签名验签测试...
签名: MEUCIBCSKMUxoCQJ8XYEyDPEE0JhMagL3e86/yNKg59CSCeuAiEAh3aY9ve1QmoFFre8P0oxn09m12Y/uBdz3YxjNY2GHQ4=
签名长度: 71 字节
验签结果: true

签名的随机性

这里有一点要注意的是，就是sm2生成签名的随机性。看下面这个代码例子：

// 同一个字符串，连续进行3次签名，输出对应的字符串
byte[] signature = SM2SignUtil.sign(privateKey, data);
            byte[] signature2 = SM2SignUtil.sign(privateKey, data);
            byte[] signature3 = SM2SignUtil.sign(privateKey, data);
            System.out.println("   签名: " + Base64.getEncoder().encodeToString(signature));
            System.out.println("   签名2: " + Base64.getEncoder().encodeToString(signature2));
            System.out.println("   签名3: " + Base64.getEncoder().encodeToString(signature3));

输出结果：

6. 签名验签测试...
签名: MEYCIQDNzUMl3RfBLYm3z9KDiJLStoPDiyiy2V11N6TG99yMVgIhAMUpI8OiQaJheu9Az1yushELYk5qW5wUaJHma6W5Bl40
签名2: MEUCIQDwdJscL41NivbakgUTeS/je9Ye1vu0HNS+1FNasYpaYQIgWcExMNyAUu9UrcoxJ35sh8msp5DL5odp/hpLRHw0wIY=
签名3: MEUCIBt1ReWXtr9GAcOh6Sd8vjX2xPh8XpJpp7uZaQlzj9SRAiEAyMBXbmfsstQx8tb8WOcjZf+51eGQ0zu754ulfIOXcb8=

细心的会你发现，输出的结果里面每次签名都是不一样的（同样的明文），这一点跟RSA是有区别的：SM2算法在数字签名时，同样的报文每次签名都会得到不同的结果，称为SM2签名的随机性原理！

SM2签名算法中包含一个随机数k，每次签名时都重新生成：

签名过程：
1. 计算消息摘要 e = Hash(Z || M) // Z是用户标识等
2. 生成随机数 k ∈ [1, n-1] // n是椭圆曲线阶数
3. 计算点 (x₁, y₁) = k·G // G是椭圆曲线基点
4. 计算 r = (e + x₁) mod n
5. 计算 s = ((1+d)⁻¹ · (k - r·d)) mod n // d是私钥
6. 签名结果为 (r, s)

关键点：每次签名都重新生成随机数k，所以每次的(r, s)都不同。

为什么SM2需要随机签名？

安全优势

抵抗重放攻击：攻击者无法复制签名用于其他交易
防止签名分析：无法通过多个相同签名分析出私钥
前向安全性：即使一次签名的随机数被破解，不影响其他签名

与RSA的区别

特性	RSA签名	SM2签名
确定性	相同的输入总是产生相同的输出	相同的输入产生不同的输出
随机数使用	不使用随机数	必须使用随机数
安全基础	大数分解难题	椭圆曲线离散对数难题
签名长度	固定（如256字节）	固定（如64字节）