LeetCode.5 最长回文子串

原题

https://leetcode-cn.com/problems/longest-palindromic-substring/

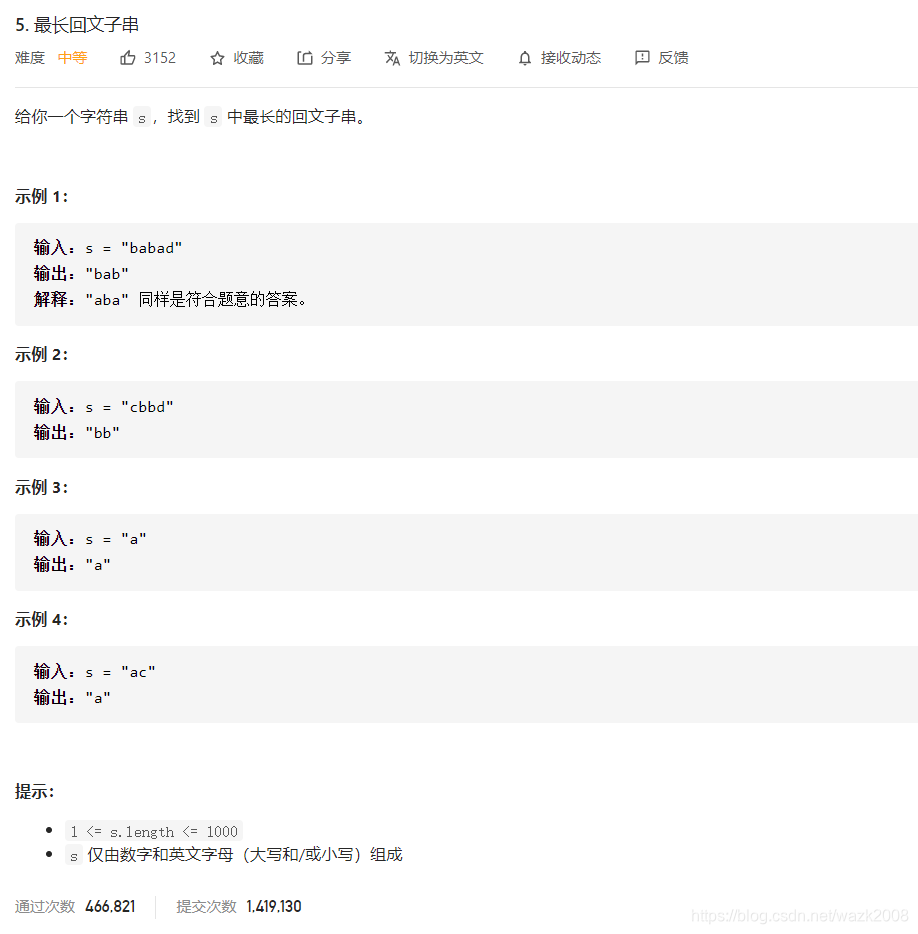
这里罗列出三种解法，分别是：①暴力求解法 ②中心扩散法 ③动态规划法
废话不多说，直接上代码，思路都在代码里。
暴力求解法

public class TestLeeCode {

    public static void main(String[] args) {
        String s = "ABBABB";
        for (int i = 0; i < str.length()-1; i++) {
            for (int j = i+1; j < str.length(); j++) {
                if ( checkHuiWen(str,i,j) ) {
                    System.out.println( str.substring(i,j+1) );
                }
            }
        }
	}
	
	public static boolean checkHuiWen(String str,int begin,int end){
        int endIndex = end;

        for (int i = begin; i <= (begin+end-1)/2; i++) {
            if ( !(str.charAt(i) == str.charAt(endIndex)) ) {
                return false;
            }
            endIndex = endIndex - 1;
        }
        return true;
    }
}

中心扩散法

public class TestLeeCode {

    public static void main(String[] args) {
        String s = "ABBABB";
        if (s.length() <= 1) {
            System.out.println(s);
        }
        int begin = 0;
        int maxLen = -1;
        for (int i = 0; i < s.length()-1; i++) {
//            奇数，判断子串为奇数，中心是某一个字符
            int oddLen = checkHuiWen1(s, i, i);
//            偶数，判断子串为偶数，中心是某两个字符中
            int evenLen = checkHuiWen(s,i,i+1);
            int curMaxLen = Math.max(oddLen,evenLen);
            if (maxLen < curMaxLen) {
                maxLen = curMaxLen;
                begin = i - (maxLen-1)/2;
            }
        }
        System.out.println(s.substring(begin,begin+maxLen));
	}
	
	public static int checkHuiWen(String str,int leftIndex,int rightIndex){
//        如果 left = right 回文中心是一个字符，回文串的长度是奇数
//        如果 fight = left + 1 回文中心是两个字符，回文串的长度是偶数

        int left = leftIndex;
        int right = rightIndex;

        int len = 0;
        while (left>=0 && right<str.length()){
            if (str.charAt(left) == str.charAt(right)){
                left--;
                right++;
                len+=2;
            } else {
                break;
            }
        }
       if (len != 0 && leftIndex == rightIndex) {
            len--;
       }
        return len;
    }
}

动态规划法

public class TestLeeCode {

    public static void main(String[] args) {
        String s = "ABBABB";
        String str = checkHuiWen(s);
        System.out.println(str);
	}
	
    /**
     * 将i,j范围内的子串回文转化为 i+1,j-1位置内的子串回文（i,j表示字符串下标）
     * @param str
     * @return
     */
    public static String checkHuiWen(String str){
        int len = str.length();
        if (len < 2) {
            return str;
        }

        int maxLen = 1;
        int begin = 0;

//        dp[i][j] 表示 str[i..j] 是否是回文数字
        boolean[][] dp = new boolean[len][len];
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

//        填写二维数组的左下角(i < j)
        for (int j = 1; j < len; j++) {
            for (int i = 0; i < j; i++) {
                if (str.charAt(i) != str.charAt(j)) {
                    dp[i][j] = false;
                } else {
//                    当前字符串个数为小于3的时候，直接赋值为true
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
//                        动态转化
                        dp[i][j] = dp[i+1][j-1];
                    }
                }

                if (dp[i][j] == true && (j-i+1)>maxLen) {
                    maxLen = j-i+1;
                    begin = i;
                }

            }
        }
        return str.substring(begin,begin+maxLen);
    }
}