目录
1. 题目介绍
给你一个字符串s, 找到s中最长的回文子串(子字符串 是字符串中连续的 非空 字符序列。)。
示例 :
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
1 <= s.length <= 1000s仅由数字和英文字母组成
2. 几种方法:
2.1 方法一:动态规划
2.1.1 思路
首先可以通过暴力(动态规划dp),将每一段子字符串都判断下是否为回文,同时更新最大长度。
2.1.1.1 设置重要变量
可以设置变量1.begin作为结果字符串的开始索引;2.maxLen作为最大回文子串长度。
2.1.1.2 确定返回值
最后返回的最长的回文子字符串为s.substring(begin, begin + maxLen);
例如最长的回文子字符串"aba":begin为1、maxLen为3,
s.subString(1,4):左闭右开--->索引为1到3的位置,即"aba"。
2.1.1.3 二维dp表
i和j可以构成一个len*len的2维dp数组:横轴代表i,纵轴代表j,
坐标(i,j)代表从索引为i到索引为j的子字符串,例如(1,3)代表"aba"。
其中i一定是 <= j的, 即我们只需要关注对角线(橙色)上方(蓝色)区域。
dp数组内的值为true或者false:为true则表示对应坐标范围的子字符串为回文字符串。
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 |
2.1.1.4 规律
接下来我们寻找一下规律:
1.由于单个字符构成的字符串一定是回文的,因此对角线值为true,用1表示。
2.当两个字符相同的时候:
①如果这个子字符串长度<=3,如"bab",它肯定是回文;
②如果子字符串长度>3,如"babab",最左边和最右边的"b"都相同,那么这个字符串是否回文会取决于它的中间的字符串"aba"是否为回文,即dp[i+1][j-1]是否为true,对应的dp表格内,它将会依赖于左下方的位置。
3.如果确定是回文,那么我们需要判断,此时的子字符串的长度是否是更长的,如果是则更新最大长度和开始索引。
4.遍历顺序:由于dp[i][j]是否为true将会依赖于它的左下角dp[i+1][j-1],因此遍历顺序需要从下到上,每一行从左到右进行遍历。
接下来展示完整代码并且附上详细注释:
2.1.2 代码
本题用Java写的,其他语言为根据原Java代码用GPT生成,仅供参考。
Java:
public class Leetcode_5_LongestPalindromicSubstring {
public static String longestPalindrome(String s) {
int len = s.length();
int begin = 0; // 结果字符串的开始索引
int maxLen = 1; // 最大长度 字符串最短为1 因此初始化为1
boolean[][] dp = new boolean[len][len];
// 由于dp[i][j]依赖于它的左下角dp[i+1][j-1], 因此遍历顺序为从下到上, 每一行从左到右边
// 为什么i为len-2, 从倒数第2行开始; j从i+1开始
// 由dp表所示对角线(橙色部分)可以提前确定为true, 因此无需多余判断
for (int i = len-2; i>=0; i--) {
for (int j = i+1; j < len; j++) {
char a = s.charAt(i);
char b = s.charAt(j);
// 两个字符相同--->同时(字符串长度<= 3, 可以直接写成j - i <= 2) 或者两个字符中间夹着的子字符串已经是回文了
if (a == b && (j - i + 1 <= 3 || dp[i + 1][j - 1])) {
// 标识这个子字符串为回文字符串
dp[i][j] = true;
// 如果子字符串长度大于了最大长度
if (j - i + 1 > maxLen) {
// 更新最大长度以及开始索引
maxLen = j - i + 1;
begin = i;
}
}
}
}
// 返回指定区间的子字符串 substring函数为左闭右开 最终begin为1 maxLen为3 substring(1,1+3)为"aba"
return s.substring(begin, begin + maxLen);
}
}C++:
#include <string>
#include <vector>
using namespace std;
class Solution {
public:
static string longestPalindrome(string s) {
int len = s.size();
if (len < 2) return s;
int begin = 0; // 结果字符串的开始索引
int maxLen = 1; // 最大长度,字符串最短为1,因此初始化为1
vector<vector<bool>> dp(len, vector<bool>(len, false));
// 由于 dp[i][j] 依赖于左下角 dp[i+1][j-1],因此遍历顺序为从下到上,每一行从左到右
// 为什么 i 为 len-2,从倒数第2行开始;j 从 i+1 开始
// 由 dp 表所示对角线(橙色部分)可以提前确定为 true,因此无需多余判断
for (int i = len - 2; i >= 0; --i) {
dp[i][i] = true; // 单个字符一定是回文
for (int j = i + 1; j < len; ++j) {
char a = s[i];
char b = s[j];
// 两个字符相同 ---> 同时(字符串长度 <= 3,可以直接写成 j - i <= 2)
// 或者两个字符中间夹着的子字符串已经是回文了
if (a == b && (j - i + 1 <= 3 || dp[i + 1][j - 1])) {
dp[i][j] = true; // 标识这个子字符串为回文字符串
if (j - i + 1 > maxLen) { // 如果子字符串长度大于了最大长度
maxLen = j - i + 1; // 更新最大长度以及开始索引
begin = i;
}
}
}
}
// 返回指定区间的子字符串
// substr 函数为左闭区间 [begin, begin + maxLen)
return s.substr(begin, maxLen);
}
};JS:
/**
* @param {string} s
* @return {string}
*/
var longestPalindrome = function (s) {
const len = s.length;
if (len < 2) return s;
let begin = 0; // 结果字符串的开始索引
let maxLen = 1; // 最大长度,字符串最短为1,因此初始化为1
const dp = Array.from({ length: len }, () => Array(len).fill(false));
// 由于 dp[i][j] 依赖于左下角 dp[i+1][j-1],因此遍历顺序为从下到上,每一行从左到右
// 为什么 i 为 len-2,从倒数第2行开始;j 从 i+1 开始
// 由 dp 表所示对角线(橙色部分)可以提前确定为 true,因此无需多余判断
for (let i = len - 2; i >= 0; --i) {
dp[i][i] = true; // 单个字符一定是回文
for (let j = i + 1; j < len; ++j) {
const a = s[i];
const b = s[j];
// 两个字符相同 ---> 同时(字符串长度 <= 3,可以直接写成 j - i <= 2)
// 或者两个字符中间夹着的子字符串已经是回文了
if (a === b && (j - i + 1 <= 3 || dp[i + 1][j - 1])) {
dp[i][j] = true; // 标识这个子字符串为回文字符串
if (j - i + 1 > maxLen) { // 如果子字符串长度大于了最大长度
maxLen = j - i + 1; // 更新最大长度以及开始索引
begin = i;
}
}
}
}
// 返回指定区间的子字符串
// slice 为左闭右开区间 [begin, begin + maxLen)
return s.slice(begin, begin + maxLen);
};2.1.3 提交通过
可以看到时间消耗很大,因为这是通过dp暴力求解,后续本文将会继续补充更快的解法。
先睡觉觉咯。
--------------------------------------------------------------------------------------------------------------------------------
2.2 方法二:中心扩散法(双指针)
2.2.1 思路
方法一的动态规划中,判断一个子串是否为回文子串,除了左右两边字符相同,它将会依赖于两个字符夹着的中间的子串。
接下来我们换一种思路,从中间往左右两边扩散。
对于字符串"babad", 长度为5,
我们可以这样思考,对于中间的字符'b', 它肯定是回文的,
接下来我们在判断它的左右两边, 都是'a', 那么'aba'也是回文,
接下来继续扩散, ‘b’ != 'd', 因此在这一轮遍历中, 得到的最长回文子串为'aba'。
设置变量和返回值都与方法一相同, 就不赘述了。
2.2.2 代码
2.2.2.1 错误示范
public static String longestPalindrome_CentralDiffusionMethod(String s) {
int n = s.length();
int maxBegin = 0;
int maxLen = 0;
for (int i = 0; i < n; i++) {
// 左指针, 从 i 开始
int l = i;
// 右指针,也从 i 开始
int r = i;
// 当左右指针在字符串范围内且对应字符相等时,继续向两边扩展
while (l >= 0 && r < n && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
// 因为上面的 while 循环结束时,l 和 r 已经越界了,所以要回退一步
l++;
r--;
// 比较当前找到的回文子串长度和之前记录的最长回文子串长度
if (maxLen <= r - l + 1) {
maxLen = r - l + 1;
maxBegin = l;
}
}
return s.substring(maxBegin, maxBegin + maxLen);
}接下来 我们来手动模拟一下:
1. i=0开始遍历, 开始while循环, l和r都没有越界,并且两边字符相等, 此时两边收缩。
此时 l和r越界了, while循环结束, 此时l和r需要回溯一下, 因为还需要记录这一轮的有效子回文 串。
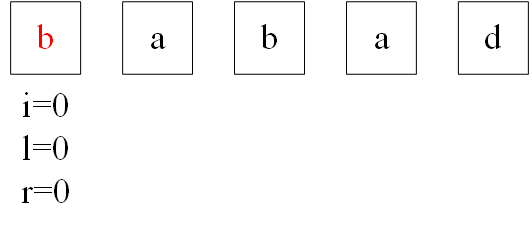
2.i=1开始遍历, 话不多说, while判断成功,l和r往两边扩散-> l = 0, r = 2;
然后while循环又判断成功-> l = -1, r = 3, while结束, l和r又回溯, 记录这一轮的回文子串"bab"。
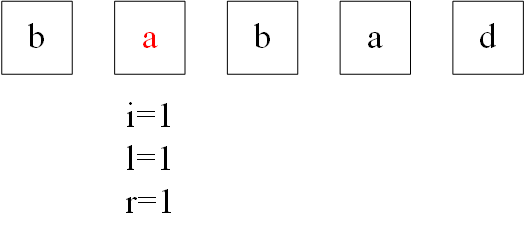
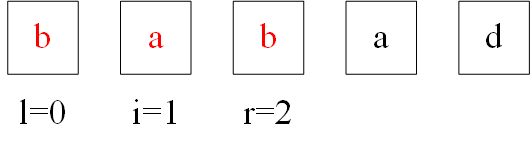
后续类似, 让我们运行一下逝世:

唉怎么不对啊?
仔细琢磨, 刚刚给出的代码如果按照"cbbd"的话, 它只能判断出单个字符的两边是否相等。
如第一个'b'的两边'c'和'b'不同, 第二个'b'的两边'b'和'd'不同。
哦哦哦哦哦!
回文串的中心可能是一个字符(如 "cbd" 的中心是 'b'),也可能是两个字符(如 "cbbd" 的中心是 "bb")。
那么我们在写代码的时候, 两个字符串的也要去处理一下:
我们多整一个参数j, 用于控制中心的字符串是单个还是两个。
2.2.2.2 正确示范
public static String longestPalindrome_CentralDiffusionMethod(String s) {
int n = s.length();
int maxBegin = 0;
int maxLen = 0;
for (int i = 0; i < n; i++) {
// j = 0 表示中心节点只有 i,即回文串中心是单个字符;
// j = 1 表示中心节点有两个 i 和 i + 1,即回文串中心是两个字符
for (int j = 0; j <= 1; j++) {
// 左指针,初始指向中心位置
int l = i;
// 右指针,根据 j 的值确定初始位置
int r = i + j;
// 当左右指针在字符串范围内且对应字符相等时,继续向两边扩展
while (l >= 0 && r < n && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
// 回溯到回文字符串的上一步起始位置
// 因为上面的 while 循环结束时,l 和 r 已经越界了,所以要回退一步
l++;
r--;
// 比较当前找到的回文子串长度和之前记录的最长回文子串长度
// 这里如果不取等号, 那么返回的子串将会是对于这个长度, 第一次记录的子串
if (maxLen <= r - l + 1) {
maxLen = r - l + 1;
maxBegin = l;
}
}
}
return s.substring(maxBegin, maxBegin + maxLen);
} 哎哎哎哎哎, 过啦!
2.2.2.3 多逼逼一句
对于示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
对于最长的回文子串, 可能有多个, 我们当前代码打印出来的结果是"aba",
那么如果同样长度的子串, 我们需要保留最开始记录的子串, 怎么改?
很简单, 在判断是否更新的时候, 把等号去掉就行
取等号的话, 每次出现同样的最长长度,都要更新一遍了。
// 比较当前找到的回文子串长度和之前记录的最长回文子串长度
// 这里如果不取等号, 那么返回的子串将会是对于这个长度, 第一次记录的子串
if (maxLen <= r - l + 1) {
maxLen = r - l + 1;
maxBegin = l;
}本题用Java写的,其他语言为根据原Java代码用GPT生成,仅供参考。
其他语言代码:
C++:
#include <string>
std::string longestPalindrome_CentralDiffusionMethod_true(const std::string& s) {
int n = s.length();
int maxBegin = 0;
int maxLen = 0;
for (int i = 0; i < n; i++) {
// j = 0 表示中心节点只有 i,即回文串中心是单个字符;
// j = 1 表示中心节点有两个 i 和 i + 1,即回文串中心是两个字符
for (int j = 0; j <= 1; j++) {
// 左指针,初始指向中心位置
int l = i;
// 右指针,根据 j 的值确定初始位置
int r = i + j;
// 当左右指针在字符串范围内且对应字符相等时,继续向两边扩展
while (l >= 0 && r < n && s[l] == s[r]) {
l--;
r++;
}
// 回溯到回文字符串的上一步起始位置
// 因为上面的 while 循环结束时,l 和 r 已经越界了,所以要回退一步
l++;
r--;
// 比较当前找到的回文子串长度和之前记录的最长回文子串长度
// 这里如果不取等号, 那么返回的子串将会是对于这个长度, 第一次记录的子串
if (maxLen <= r - l + 1) {
maxLen = r - l + 1;
maxBegin = l;
}
}
}
return s.substr(maxBegin, maxLen);
}JS:
function longestPalindrome_CentralDiffusionMethod_true(s) {
let n = s.length;
let maxBegin = 0;
let maxLen = 0;
for (let i = 0; i < n; i++) {
// j = 0 表示中心节点只有 i,即回文串中心是单个字符;
// j = 1 表示中心节点有两个 i 和 i + 1,即回文串中心是两个字符
for (let j = 0; j <= 1; j++) {
// 左指针,初始指向中心位置
let l = i;
// 右指针,根据 j 的值确定初始位置
let r = i + j;
// 当左右指针在字符串范围内且对应字符相等时,继续向两边扩展
while (l >= 0 && r < n && s[l] === s[r]) {
l--;
r++;
}
// 回溯到回文字符串的上一步起始位置
// 因为上面的 while 循环结束时,l 和 r 已经越界了,所以要回退一步
l++;
r--;
// 比较当前找到的回文子串长度和之前记录的最长回文子串长度
// 这里如果不取等号, 那么返回的子串将会是对于这个长度, 第一次记录的子串
if (maxLen <= r - l + 1) {
maxLen = r - l + 1;
maxBegin = l;
}
}
}
return s.substring(maxBegin, maxBegin + maxLen);
}宝宝们觉得我的屎山代码有用的话,可以点个赞么么哒!





















 3929
3929










