【数据结构-浙大-陈越】2.1 线性表、顺序存储及其操作

this figure shows how data types and data structures are related

引子：一元多项式表示

分析多项式特点，找到关键数据，进行表示：

• 多项式次数 n
• 各项的系数 和 指数

方法1：顺序存储结构直接表示

数组各分量对应多项式各项。

好处是：每个下标对应多项式中的一项，多项式相加运算 == 两个数组对应分量相加。缺点是：当多项式次数n很大，但中间很多项为0时，十分浪费空间。比如

方法2：顺序存储结构表示非零项

每个非零项主要包含两个信息：系数 和 指数 ，于是可以将 一个多项式看作由二元组(, )组成的集合。

使用结构数组表示：数组分量包含 系数 和 指数 ，比如，可表示为有序数组 。

当做加法运算时，对p1和p2进行合并排序，联想到leetcode 88：合并两个有序数组，排序思想是 使用双指针，比较数组头部指数，并将较大的放在前面，移动指针，再继续比较，直到遍历完数组中所有元素。

方法3：链表结构存储非零项

链表中每个结点 存储多项式的一个非零项，包括系数和指数两个数据域 和 一个指针域。类似 (coef, expon, link).

启示：

• 同一个问题 可以有不同的表示 (存储)方法
• 对有序线性序列进行组织和管理

线性表及顺序存储

什么是线性表 (Linear List)？

由同类型数据元素构成的 有序序列的线性结构。

• 表中元素个数 称为线性表的长度；
• 线性表没有元素时，称为空表；
• 表的起始处为表头，结束位置为表尾

线性表的抽象数据类型描述

类型名称: 线性表 Linear List

数据对象集：同类型数据  构成的有序序列

线性表的基本操作有：

• List MakeEmpty() ：初始化空线性表 L
• ElementType FindKth(int K, List L)：根据索引K，返回对应元素
• int Find(ElementType X, List L)：在 L 中查找X 第一次出现的位置
• void Insert(ElementType X, int i, List L)：在索引 i 前插入一个新元素 X
• void Delete(int i, List L)：删除指定索引 i 的元素
• int Length(List L)：返回 L 的长度

线性表如何存储？如何实现线性表的基本操作？

方法1：利用数组Array存放

使用数组的 连续存储空间，顺序存放线性表中的各个元素

数组实现线性表代码：github

方法2：使用链表实现线性表顺序存储

不要求逻辑上相邻的两个元素在物理上也相邻，即存放数据时不必要求一定使用连续的内存空间，元素之间的逻辑关系是通过"链"建立起来的。

• 插入、删除元素时，不需要移动元素，只需要修改 链；

链表实现线性表代码：github

广义表与多重链表

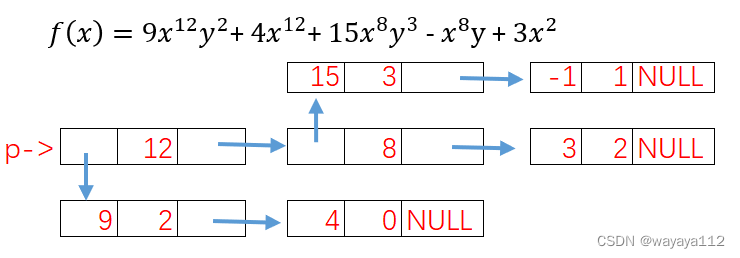
二元多项式表示问题

 

什么是广义表（generalized list）？

线性表的推广，元素不仅可以是单元素，也可以是子表sublist。

tag：标志域，0表示结点为单元素，1表示结点为子表

union：联合，子表指针域sublist 与 单元素数据域 data 复用，即共用存储空间

多重链表

链表中的结点可能同时隶属于多个链。多重链表中结点的指针域会有多个，比如包含Nex和SubList 两个指针域；但是，双向链表包含了2个指针域，但它不是多重链表。

多重链表用途广泛，比如 树、图这样相对复杂的数据结构都可以采用多重链表方式来实现存储。

使用典型的多重链表—十字链表来存储 稀疏矩阵(二维数组)

• 只存储矩阵非0元素项，故结点的数据域包括：行row，列col，值value
• 每个结点通过两个指针域，将同行、同列串起来。每个term结点或head结点由一个同行循环链表和一个同列循环链表组成；
  • 行指针，或向右指针 right
  • 列指针，或向下指针 down

   

• 使用标识域tag 来区分 头结点head 和 非0元素结点term；

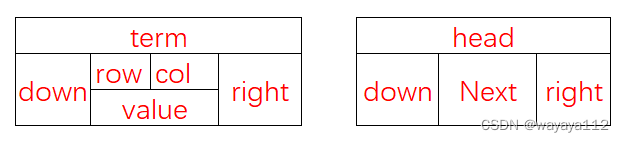
使用union 将这两个指针域 放在同一个空间中。