本文通过一个图示例子对比了贪心算法和动态规划解决最短路径问题的不同策略。贪心算法每次选择眼前最优解，得出31的路径，而动态规划记录到达每个位置的最优值，最终得到全局最优解18。文章强调贪心不一定能得到全局最优解，而动态规划确保全局最优。此外，还探讨了动态规划在矩阵连乘积问题中的应用，指出在特定情况下局部最优可推出全局最优。
先来看一个例子：
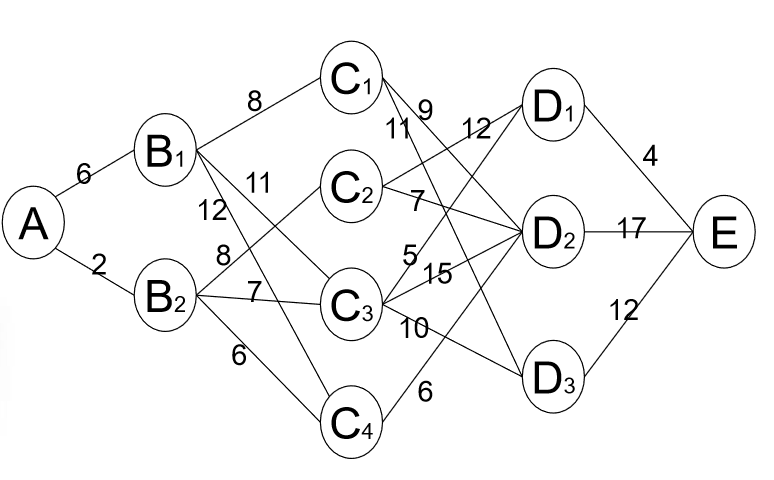
如图，各结 点代表城市， 两结点间连 线上数字表 示城市间的 距离。试找出从结点A到 结点E的最短距离
贪心：
首先，这题如果用贪心来看的话，则为A->B2，B2->C4, C4->D2, D2->E, 这应该没有争议吧（如果硬要挑毛病的话那么就假设是有向图，只能往右走），这样得出来的结果是31，这是贪心的结果，即每次考虑眼前的最优解。
动态规划：
如果从动归的角度来看的话，那么它的选择就不是线性的了，而是在到达B、C、D、E这四个阶段时从前面记录的所有相邻节点所记录的最短路径中选择下一条最短路径（总结得过于繁琐），怎么理解呢？我们一步步来看。
我们从A开始，在贪心和动归眼里都是两条路，但不同的是贪心选择了A->B2这条最短路径，就遗忘了还有A->B1这个选择，那么它的下一步就只能从B2这个节点开始选择下一步的最短路径；而对于动态规划来说，它需要记录的不是从A开始的下一条最短路径，它要记录的是到从A开始的到B1所走过的最短距离和到B2所走过的最短距离，即B1=6，B2=2；然后下一步，进入到第二阶段，即从B开始，它首先从B1开始，走向C1，然后记录到C1的最短距离，即C1=8，然后是C3=17，C4=13；然后从B2开始走，C2=10，然后到C3的时候发现以前的值（即从B1到C3）比现在的大，
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
