Scratch编程实现DFS递归调用出错分析

今年中小学人工智能夏令营竞赛选拔中有一道题目，大意是输入一个小于10的自然数n，编程展示1到n之间所有自然数所组成的整数的列表，并对列表做排序操作。

按照数学公司，1到n之间所有自然数所组成的整数的排列数为:

• 如果n=2，组成的整数排列个数为2，即[12,21];
• 如果n=3，组成的整数排列个数为6，即[123,132,213,231,312,321]
• 如果n=10,组成的整数排列个数为3628800。

可见，限制n小于10，是为了不至于占用太多平台计算资源。

1 DFS算法简介

用Scratch编程如何解题呢？要遍历1到n之间的所有自然数，一种方法时用到DFS算法。先介绍什么是DFS算法。

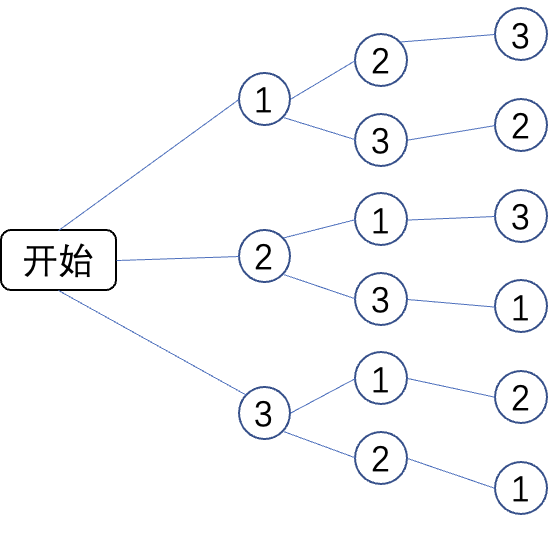
图1，DFS深度搜素算法图例

DFS算法是深度搜索算法，可以理解为一种节点连接图的遍历算法。如图1，开始时没有节点，第一层可以选择的节点有①、②、③，假定选定①；之后第二层的选择可以是②或者③，假定选择②；之后第三层的选择只能是③。到了第三层后，层数到底了，只能回退一步第二层，也就是到②，但是②的下一层只能是③，已经遍历过，只能继续回退到第一层的节点①，这之下的第二层可以选择③，再之后第三层可以选择②。到达最底层后又开始回退，这次一直回退到“开始”，也就是第0层，这一层的下一步可以选择②或者③，选择其中一个继续遍历。直到遍历完成整个节点连接图。

2 Python编程实现

算法明白后，我们首先用Python编程做软件实现。

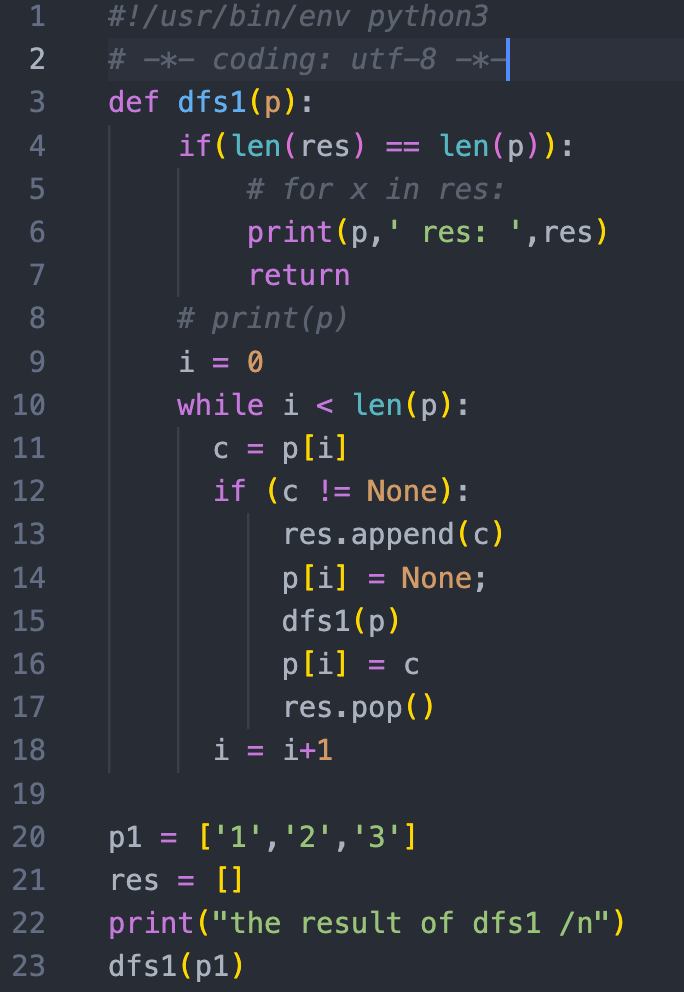
图2，python代码实现

python代码中，行20定义了字符串数组p1，行21定义了res空数组，用于存放遍历后的结果。

代码主要用到了dfs1递归函数。其要点有两个，一个是递归的结束条件，也就是行4的代码，当res的项目数等于p的项目数时，打印res中的内容。第二个要点是，DFS调用后，在继续调用前，需要进行数组p和res的回退操作，行16和17的代码就是回退操作，恢复p的内容和res的内容，以便进行下一步dfs。

行9到行18对变量i的循环表明，对p中所有元素的处理都是平等的。只要p中的元素没有候选过（行12判断是否候选过，非None），都有机会被候选（行11）

按行4的代码，当res的长度和p的长度一致时，打印输出res中的内容。然后函数返回到上一步递归调用处。

Python的运行结果见图3。可以看出程序确实实现了数组p内各元素的排列组合。

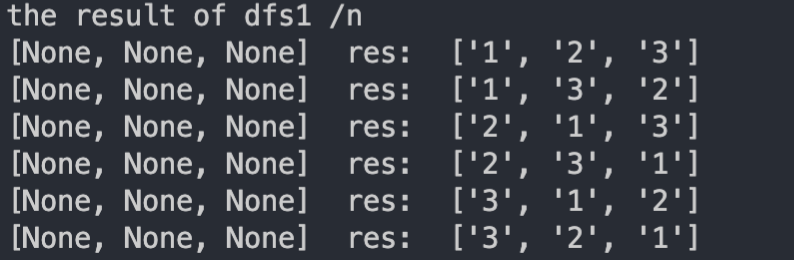
图3，python的执行结果

3 Scratch编程实现

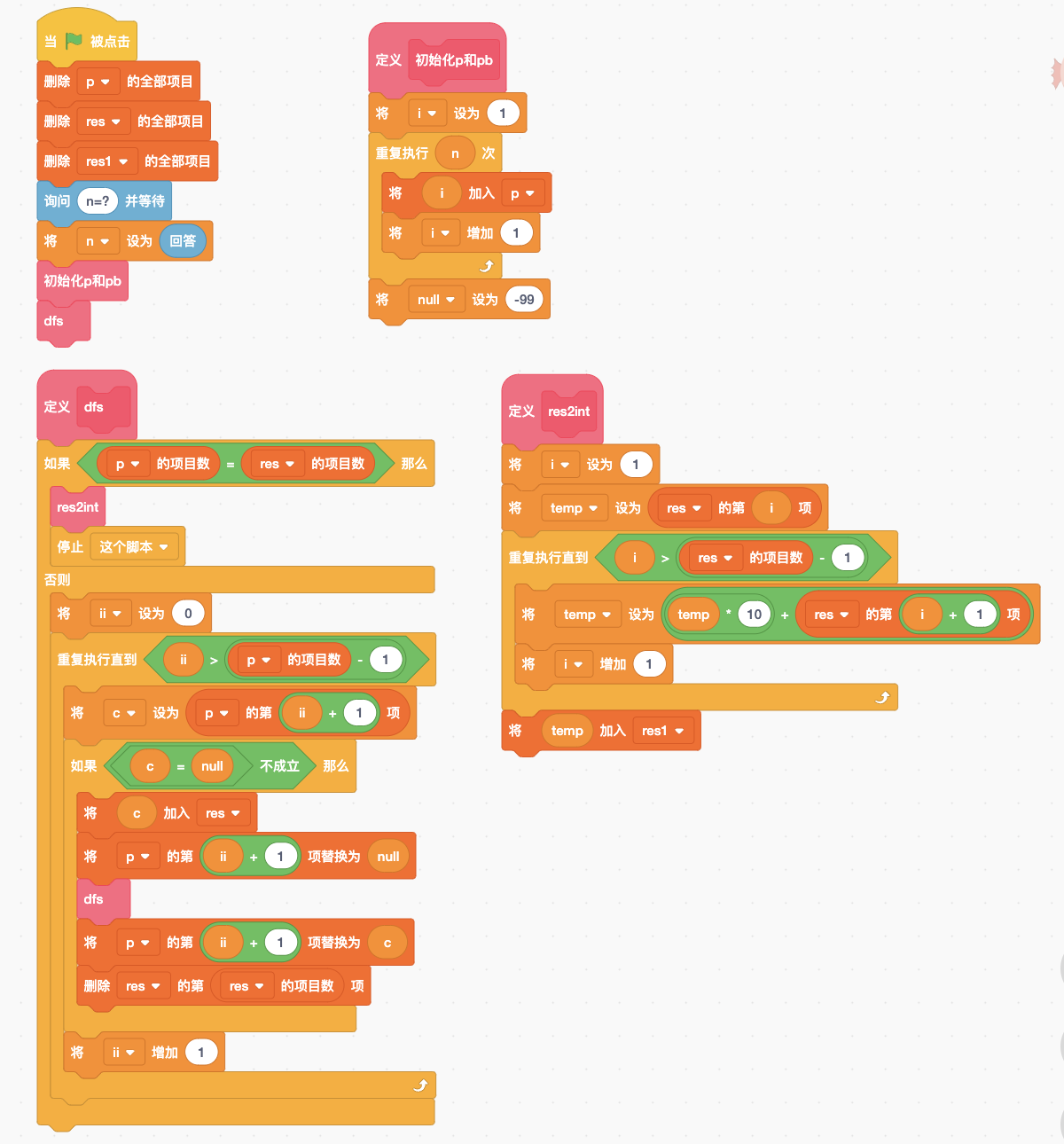
图4，Scratch编程实现，模仿python的代码，执行结果有错误。

上述Scratch图形化代码中，用到了三个列表。列表p初始化时根据输入的自然数n产生1到n之间的n个自然数，作为dfs算法的输入。列表res用于暂存列表p的遍历结果。当res的项目数等于p的项目数时，调用自定义模块res2int,将res中的项目转换成10进制整数并用堆栈方式压入到res1，列表res1展示所有遍历的排列组合，也就是题目要求的结果。

但是实际执行Scratch代码时发现res1中只能产生一个整数123，列表p中个别元素可以回退，但是回退后再执行dfs递归调用时乱套了，其中控制循环的变量ii居然出现了5（见图5），超出了循环的范围，非常奇怪。

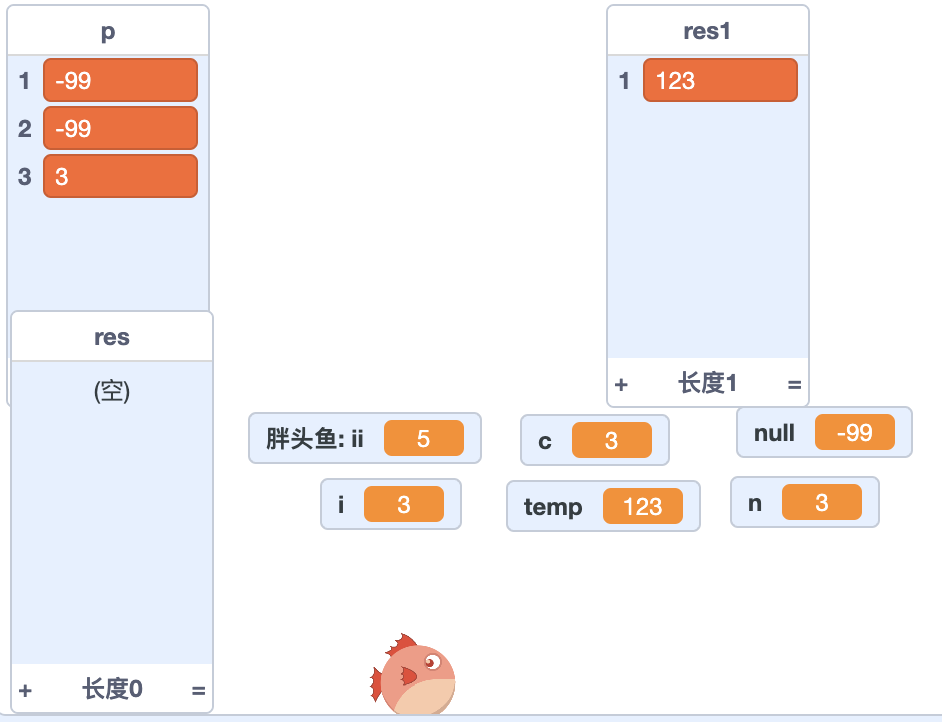
图5，Scratch递归调用出错时的结果。其中ii等于5是违背图4中循环代码逻辑的。

Scratch中的变量虽然有私有变量和公有变量之分，但这是按角色的划分。角色独有的变量为私有变量，所有角色都可以存取的变量为公有变量。Scratch中的变量没有函数作用域的限制，函数内外都可以用，或者说不同函数定义的同名变量实际是同一个变量。Scratch中可以自定义积木，但是其中用到的变量仍是全局的。因此，上述递归调用出错，高度怀疑是DFS回退时，对列表p的恢复出现了问题，其中用到的p列表的序号以及变量c（对应p中需要恢复的元素）在DFS递归回退时可能发生了变化。

为了发现和解决问题，转用CCW共创世界的Scratch编程平台（共创世界(ccw.site) - Scratch、游戏、动画、漫画、小说、编程创作社区），因为这个平台的Scratch编程可以增加“控制台”扩展模块。“控制台”中最重要的调试工具有两项。第一项“显示控制台”可以单独打开一个控制台窗口，其中可以输入调试命令和显示调试结果。第二项为“记录日志‘hello'”，这个调试积木可以插入到代码积木中，非常方便观察程序的执行位置和位置处的变量值。

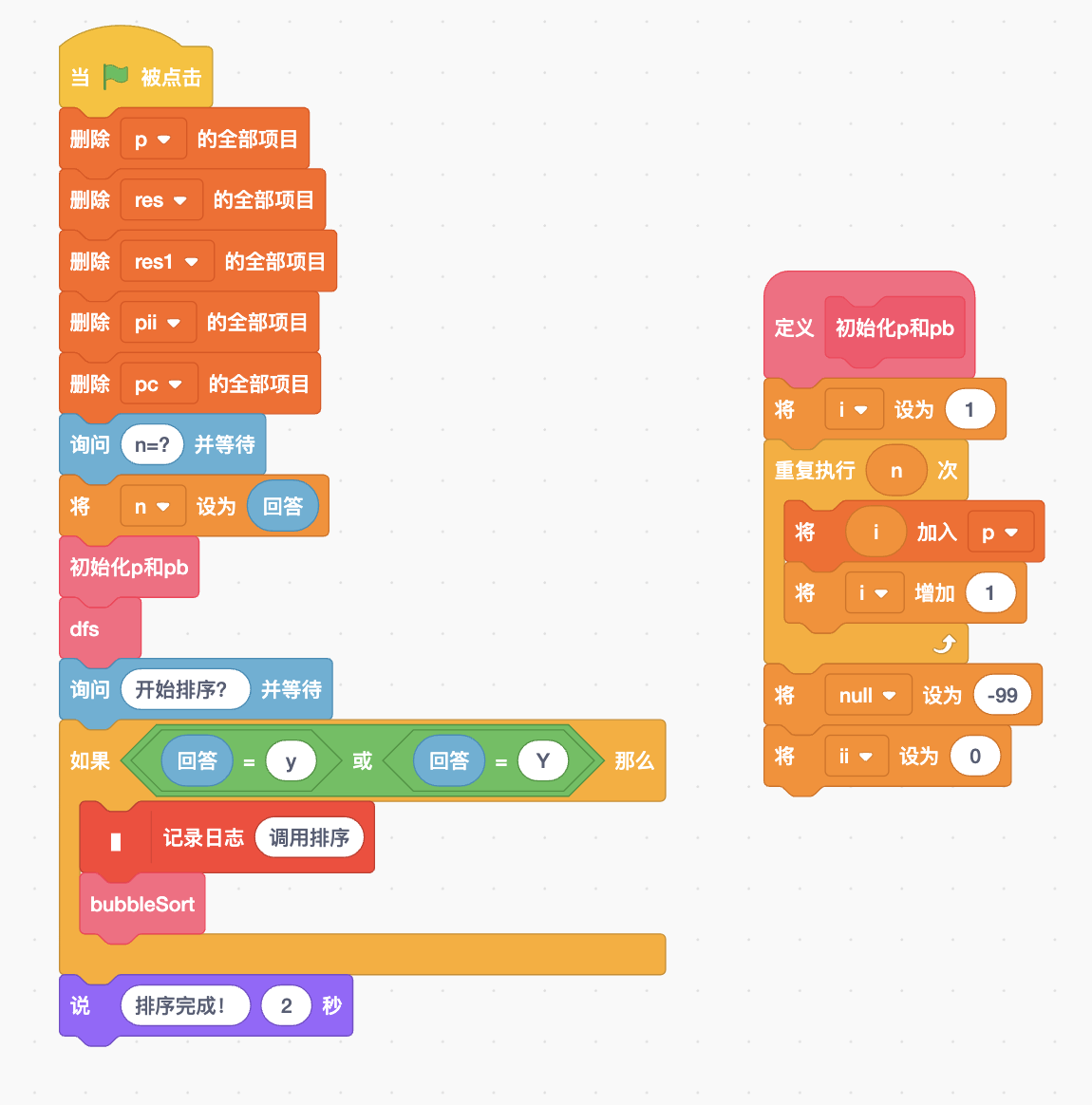
图6，最终Scratch代码实现，截图一

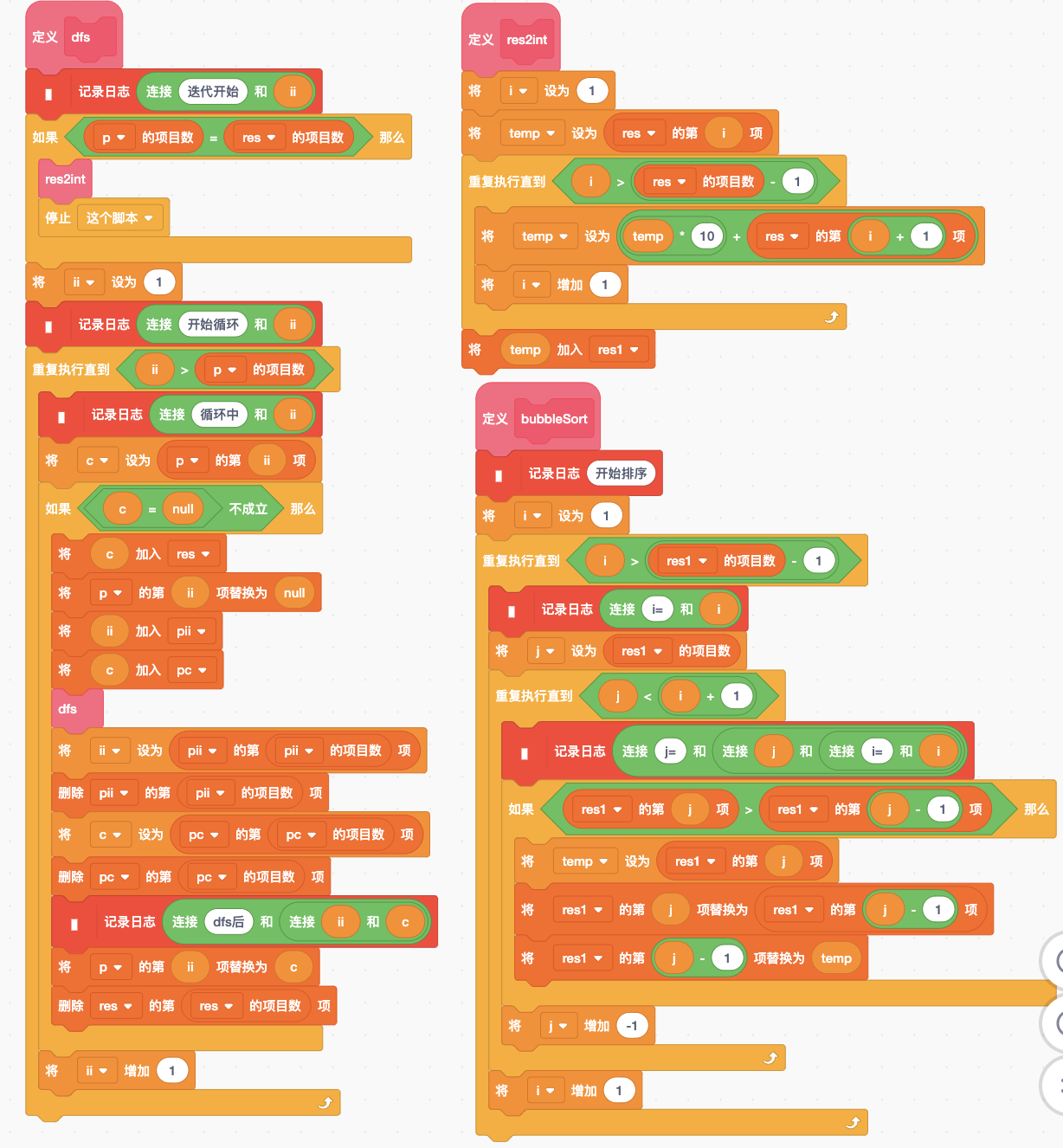
图7，最终Scratch代码实现，截图二

相比图4的代码，图6和图7图示的代码中，其DFS递归调用部分主要增加了列表pc，作为堆栈用。dfs调用前，需要将循环变量ii以及对应的p元素c压入堆栈pc；dfs调用后，需要用弹栈方式恢复ii和c的值。

图8，当n=3时，所有小于n的自然数的排练组合，一共有6种组合。

图片加载中

图9，当n=4时，所有小于n的自然数的排练组合，一共有24种组合。

从图6和图7展示的代码中，可以看到其中插入了很多调试语句，用于观察代码的执行位置和位置处的变量值。最主要显示的是DFS算法的递归调用顺序以及DFS算法回退过程中列表p内容的恢复情况等。

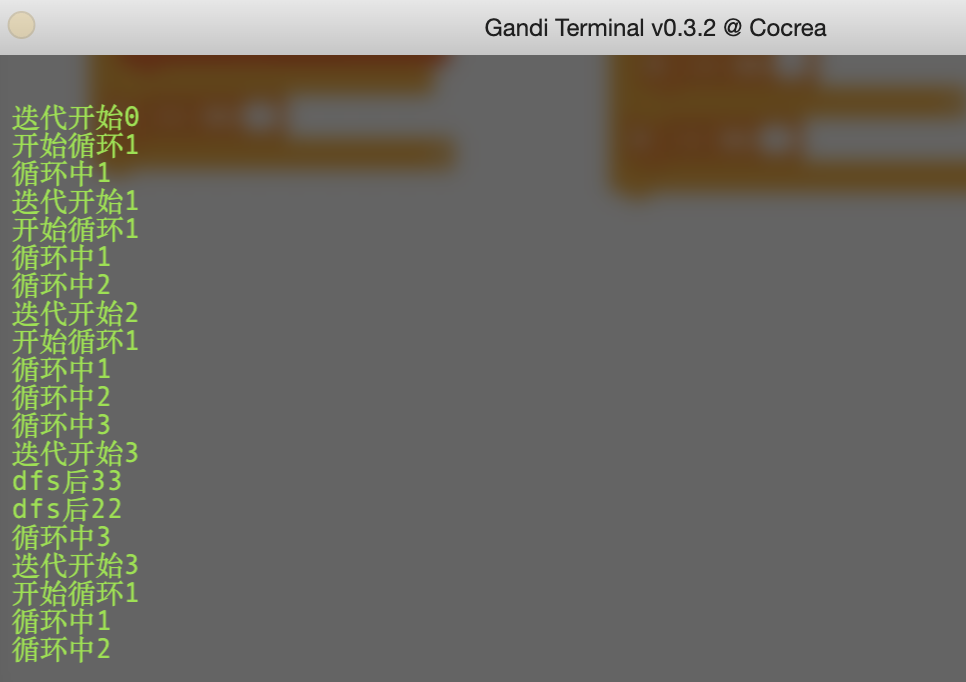
图10，Scratch扩展模块之Gandi控制台显示的调试情况

最后的代码以及运行展示在ccw平台，链接为共创世界(ccw.site) - Scratch、游戏、动画、漫画、小说、编程创作社区 。手机通过微信扫码下面的二维码（图10）也可以直接运行。

图片加载中

图10，手机微信扫码可直接在微信下运行本程序。

4 关于Scratch编程

Scratch图形化编程是一项入门门槛低但是探索天花板高的开源编程平台。我试用这个平台的初衷是想辅导自己的孩子（小学4年级）参加中小学人工智能夏令营的选拔。这个夏令营的规格很高，其中知名院士就有2位，博士教授或者知名示范中学的信息课教研老师也很有名。夏令营选拔和培训的目的是发现对人工智能有学习热情和学习能力的未来科学家。我看了其中一些人工智能通识课，内容确实不错。去年的课题是用K近邻算法进行树叶分类，要求学生自行拟定树叶多参数特征，实现基于计算机视觉的树叶识别算法。要求在经过了上千张图片的训练后，能够识别实际给出的树叶样本的分类。今年的夏令营小学部分的主题是机器博弈，考核的范围中明确要求掌握DFS算法、排序算法、二维地图之一维列表存储方法等，对小学生的要求还是挺高的。

令人遗憾的是，由于本人辅导水平有限，加上孩子这个暑假参加了篮球精英队，训练和比赛比较多。孩子时间不够，老师一知半解，我们报名的中小学人工智能夏令营最后未能通过笔试。参加考试前我们对DFS算法也只是知道大概，实操题目要求考试时在线完成，不仅对孩子是很大挑战，就是我事后编程来做，也是想了很多天才发现Scratch递归调用中的挑战。这次参加笔试的同学有1300多人，通过笔试的学生为80人，中小学两组各为40人。通过的比例还是挺高的，后生可畏呀！