本文介绍了学习型索引的概念，它利用模型预测数据分布以提高检索效率。文章详细讨论了范围索引、点索引和存在索引的实现，包括使用CDF模型、递归回归模型和混合模型，以及如何应用这些模型改进哈希映射和Bloom过滤器。
系列文章目录
学习型索引结构---开山之作学习 The Case for Learned Index Structures
目录
前言
因为实验室方向，博主在今年暑假开始学习学习型索引，记录学习过程。
一、学习型索引是什么？
首先，索引就是一个模型，一个键值对模型。B树索引，哈希索引，BitMap索引都是键-值对的映射。那这就是一个给定x,得到y的模型了。
文章中提出了一个想法-----模型可以学习查找键 (Key) 的排序顺序或结构，并使用这个信息来有效地预测值记录 (Value) 的位置或存在。也就是说用模型代替索引结构的思想。文章认为，当数据分布本身存在一定规律的时候, 就可以利用已有的规律进行检索, 而不用通用数据结构. 如有序数据, 可以用近似累计分布函数 CDF 来预测数据的位置, 累积分布函数模型的预测复杂度为 O(n). 学习型索引将索引结构看作模型, 将传统树型结构的页面大小看做是机器学习模型的最大误差, 只要使得模型的预测误差小于页面大小就等于保证了查询精度.见图一。
二、范围索引
索引结构已经是模型，因为它们可以“预测”给定键 (Key) 的值的位置。如图 [1]所示。 在这种情况下，B-Tree 提供从查找键 (Key) 到排序的值记录 (Value) 阵列内的位置的映射，并保证值记录 (Value) 位置大于等于查找到的位置。出于效率的原因，通常不会对已排序值记录 (Value) 的每个关键 (Key) 字进行索引，而只是每n 个值记录 (Value) 一个键 (Key)，即每页面的第一个键 (Key)。这有助于显着减少索引必须存储的键 (Key) 数量，而不会有任何显着的性能损失。
因此，b树是一个模型，或者在ML术语中是一个回归树:它将键映射到具有最小误差和最大误差的位置(最小误差为0，最大误差为页面大小)，并保证如果该键存在，则可以在该区域找到该键。因此，我们可以用其他类型的ML模型(包括神经网络)替换索引，只要它们也能够提供类似的关于最小和最大误差的强保证。
B-Tree 仅为存储的数据提供这种保证，而不是针对所有可能的数据。 对于新数据，B 树需要重新平衡，或者在机器学习的术语里面叫重新训练，通过训练来提供相同的误差保证。我们唯一需要做的就是对每个键 (Key) 执行训练，并记住一个位置的最好和最差的位置预测。 给定一个键 (Key)，该模型预测哪里能找到相应的值记录 (Value); 如果键 (Key) 存在，则保证处于由最小和最大误差定义的预测范围内。 因此，我们能够用任何其他类型的回归模型（包括线性回归或神经网络）代替 B 树。
2.1 范围索引模型是 CDF 模型（累积分布函数）
p=F(Key)*N
其中p为位置估计，F(Key)为估计的数据累积分布函数，用于估计观察到小于或等于查找键p (X≤Key)的键的可能性，N为键的总数。 这个观察开辟了一套全新的有趣方向：首先，它意味着任何一种索引字面上都需要学习数据分布。 B 树通过构建回归树来“学习”数据分布。 线性回归模型将通过最小化线性函数的(平方) 误差来学习数据分布。 其次，估计数据集的分布是一个众所周知的问题，学习索引可以从之前数十年的研究中受益。 第三，学习CDF 对优化其他类型的索引结构和潜在算法也起着关键作用.
2.2 解决最后一公里精度问题
构建替代 B 树的替代学习模型的关键挑战之一是最后一英里的准确性。例如，使用单个模型把误差从 100M 减少到几百这个数量级是非常困难的。 同时，将误差从 100M 降低到 10K，例如 100 * 100 = 10000 的精度实现起来还简单些，这样就可以用简单模型替换 B-Tree 的前两层。 同样的，将误差从 10k 降低到 100 是一个更简单的问题，因为模型只需要关注数据的一个子集。
提出递归回归模型(见图3)。也就是说，我们构建了一个模型层次结构，在每个阶段，模型都将键作为输入，并在此基础上选择另一个模型，直到最后阶段预测位置。更正式地说，对于我们的模型 f(x) ，其中 x 是键， y∈ [ 0 ， N ) 位置，我们假设在阶段ℓ有 
个模型。 我们在阶段 0 训练模型，f0(x) ≈ y 。 因此，阶段ℓ中的模型 k，可以写成由 
表示 ，并且被损失地训练，整个误差可以表示为如下公式：
考虑不同模型的一种方法是，每个模型对键的位置进行预测时存在一定的误差，然后使用该预测来选择下一个模型，该模型负责键空间的特定区域，以便以更低的误差进行更好的预测。然而，递归模型索引不一定是树。如图3所示，一个阶段的不同模型可能在下一阶段选择相同的模型。此外，每个模型不一定像b树那样覆盖相同数量的记录。最后，根据所使用的模型，不同阶段之间的预测不一定可以解释为位置估计，而应该被认为是选择一个对某些关键有更好知识的专家。
这种模型体系结构有几个好处:(1)它将模型大小和复杂性与执行成本分离开来。(2)它利用了易于学习数据分布的整体形状的事实。(3)它有效地将空间划分为更小的子区域，如b树，使其更容易以更少的操作实现所需的“最后一英里”精度。(4)在两个阶段之间不需要搜索过程。例如，直接使用模型1.1的输出来选择下一阶段的模型。这不仅减少了管理结构的指令数量，而且还允许将整个索引表示为TPU/GPU的稀疏矩阵乘法。
2.3混合索引
递归模型索引的另一个优点是，我们能够建立模型的混合。例如，在顶层，一个小的 ReLU 神经网络可能是最好的选择，因为它们通常能够学习大范围的复杂数据分布，模型层次结构底部的模型可能有数千个简单的线性回归模型，因为它们在空间和执行时间都不贵。 此外，如果数据特别难以学习，我们甚至可以在最后阶段使用传统的 B 树。在本文中，我们重点研究了2种模型，即具有0到2个完全连接隐藏层和ReLU激活函数的简单神经网络，层宽度高达32个神经元和b树(又名决策树)。注意，零隐藏层神经网络等价于线性回归。下面图片显示的是使用混合索引之后的优点。
三、点索引
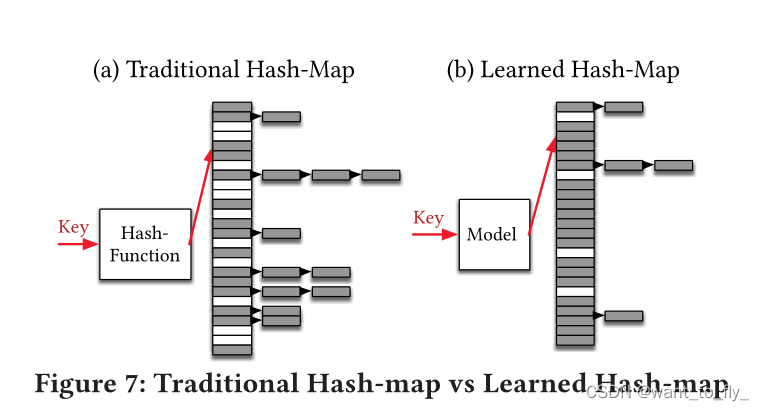
从概念上讲，哈希映射使用哈希函数来确定地将键映射到数组中的位置(参见图7(a))。任何有效的哈希映射实现的关键挑战是防止太多不同的键被映射到哈希映射中的相同位置，因此称为冲突。
哈希表面临的问题就是不完美哈希，哈希冲突高，效率低下。这里的改进也是用了之前的思想，用那个分层模型。使用CDF累计分布函数。与范围索引相比，我们的目标不是紧凑地存储记录或严格排序。相反，我们可以根据哈希映射的目标大小M来缩放CDF，并使用h(K) = F(K) * M，键K作为我们的哈希函数。如果模型F完全学习了键的经验CDF，则不存在冲突。此外，哈希函数与实际的哈希映射体系结构是正交的，可以与单独的链或任何其他哈希映射类型结合使用。
四、存在索引
Bloom过滤器，一种空间有效的概率数据结构，用于测试元素是否是集合的成员。它们通常用于确定密钥是否存在于冷存储中。通俗的讲，就是你给它一个key,让它告诉你存不存在。但是注意一点的是：它告诉这个key不存在，那就一定不存在，如果告诉你存在，那就可能不存在，具有假阳性的特点。
在内部，Bloom过滤器使用大小为m的位数组和k个散列函数，每个散列函数将一个键映射到m个数组位置中的一个(参见图9(a))。要向集合中添加一个元素，需要向k个哈希函数提供一个键，并将返回位置的位设置为1。为了测试一个键是否为集合的成员，再次将该键输入k个哈希函数以接收k个数组位置。如果这k个位置上有任何位是0，那么这个键就不是集合的成员。换句话说，布隆过滤器确实保证不存在假阴性，但有潜在的假阳性。
对于点索引来说，一个好的哈希函数应该是键之间很少有冲突的哈希函数，而对于布隆过滤器来说，一个好的哈希函数应该是键之间有很多冲突，非键之间也有很多冲突，但键和非键之间很少有冲突。
所以第一种方法就是使用CDF，形成完美空间也就是（b）。另一种就是二元分类任务（C),使用神经网络，作者想表达的就是，可以存在假阳性，但是说不存在一定要不存在，key先经过神经网络模型判断，存在就通过，不存在就进入Bloom过滤器判断。
总结
博主只是简单的看了看，还没有完全入门，估计有很多错误，或者理解错的地方，请大家见谅。接下来准备看针对开山之作的改进的一篇论文，应该也是同一个团队发的。ALEX: An Updatable Adaptive Learned Index，这个是解决针对这篇文章的有序+只读的适用情况。具体的代码演练啥的也没有尝试过，再深入了解之后，找找资源，尝试写写。
扫一扫
473
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
