快速排序详解：冒泡与三数取中优化-优快云博客

本文链接：https://blog.youkuaiyun.com/wangzai32100/article/details/125648563

交换排序

基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

冒泡排序

两层for循环

for（）------->外层循环：控制冒泡的趟数

for（）------->内层循环：控制冒泡的方式-----用相邻的两个元素来进行比较，不满足要求时将相邻的元素进行交换，直到区间的末尾


void Swap(int* left, int* right)
{
    int temp = *left;
    *left = *right;
    *right = temp;
}

// 冒泡排序
// 时间复杂度：O(N^2)
// 空间复杂度：O(1)
// 稳定性：稳定
void BubbleSort(int array[], int size)
{
    // 控制冒泡的趟数
    // -1的目的可以少冒一趟，因为最后一次冒泡区间中只剩一个元素
    for (int i = 0; i < size - 1; ++i)           
    {
        // 具体的冒泡方式：用相邻位置的元素进行比较，如果不满足条件，就进行交换
        // j：表示前一个元素的下标
        // -1目的：j最多只能取到冒泡区间的倒数第二个元素
        for (int j = 0; j < size - i - 1; ++j)   
        {
            if (array[j] > array[j + 1])
                Swap(&array[j], &array[j + 1]);
        }
    }
}

快速排序

其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该基准值将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

将区间按照基准值划分为左右两半部分的常见方式有：

1. hoare版本

2. 挖坑法

3. 前后指针版本

//[left,right)表示待排序元素的区间
void QuickSort(int array[], int left , int right)
{
   // 判断区间之间元素是否超过一个
   if(right - left > 1)
   {
       //Partion按照基准值(区间中的某个元素)对区间进行划分，左部分<key，右侧部分>key
       //该函数返回基准值在区间中的位置
       int div = Partion1(array, left, right);
       
       //[left, right) 区间中的基准值位置已经存放好了，基准值左侧和基准值右侧不一定有序
       // 基准值的左侧： [left, div)      
       QuickSort(array, left, div);

       // 基准值的右侧： [div+1, right) 
       QuickSort(array, div+1, right);
   } 
}

数据分割：

分割方式一：hore提出快排思想的大佬

基准值取最左或最右的值

① 只要begin和end没有遇到或者没有错过（begin和end区间中有元素）

② begin从前往前后移动，找比基准值大的元素，找到就停下来

③ end从后往前移移动，找比基准值小的元素，找到就停下来

④ 交换begin和end位置上的元素

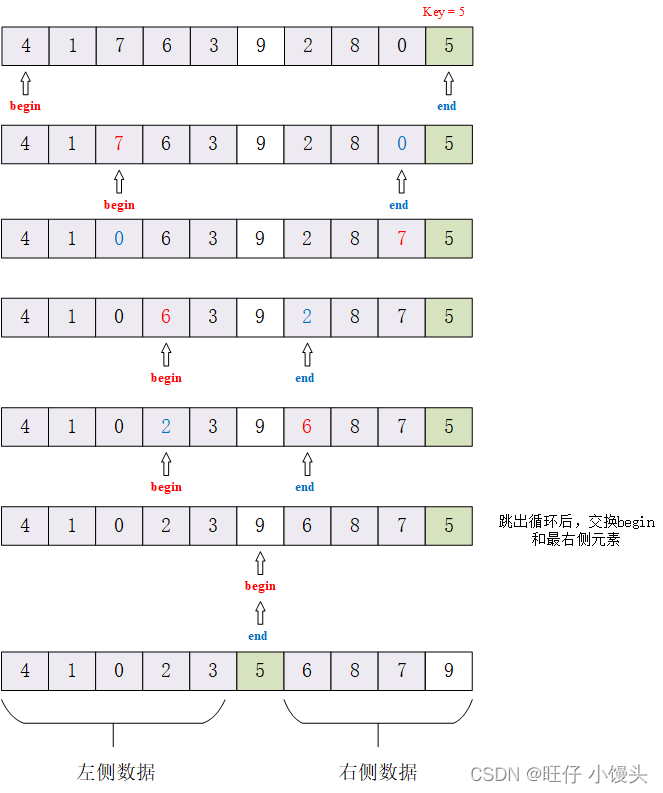
有一种极端的情况基准值恰好为最大（最小），begin（end）指针一直往后找都找不到比它大（小）的值，最终会移动到越界，所以begin和end在移动过程中还需要满足 begin < end恒成立，while(begin < end && array[begin] <= key) { begin++ }

最终begin和end会重合，当begin和right-1指向同一个位置时，就没有必要交换array[begin]和array[right-1]

// hore：提出快排思想的大佬提出的
int Partion1(int array[],int left,int right)
{
    int begin = left;
    int end = right-1;
    int key = array[right-1]; //选最右侧的元素为基准值
 
    while(begin < end)
    {
        // 让begin从前往后找，找比基准值大的元素，找到就停下来
        while(begin < end && array[begin] <= key )
            begin++;  

        // 让end从后往前找，找比基准值小的元素，找到就停下来
        while(begin < end && array[end] >= key )
            end--;
 
        // 全都找到后交换begin和end位置的元素
        Swap(&array[begin],&array[end]);
    }

    // 当begin和end重合后,先判断begin的位置是否也是right-1处，如果不在，将基准值key交换过去
    if(begin!= right-1)
        Swap(&array[begin] , &array[right-1]);

    return begin;//最终返回begin位置即为基准值的位置
}



void TestSort()
{
	int array[] = { 4, 1, 7, 6, 3, 5, 2, 8, 0, 9 };
	cout << "排序前：";
	PrintArray(array, sizeof(array) / sizeof(array[0]));
    QuickSort(array, 0 , sizeof(array) / sizeof(array[0])); // [0,10) , 10个元素下标为0-9
    cout << "快速排序后：";
    PrintArray(array, sizeof(array) / sizeof(array[0]));
}

分割方式二：挖坑法

// 挖坑法
int Partion2(int array[], int left, int right)
{
    int begin = left;
    int end = right - 1;
    int key = array[right - 1]; //选最右侧的元素为基准值,end指向它，把它挖走成为第一个坑

    while (begin < end)
    {
        // end位置形成了一个新的坑
        // 让begin从前往后找比基准值大的元素，找到后，将该位置的值填到end处的坑
        while (begin < end && array[begin] <= key)
            begin++;

        if(begin < end)
        {
            array[end] = array[begin];
            end--;
        }
        
        
        // begin位置形成了一个新的坑
        // 让end从后往前找，找比基准值小的元素，找到后，填到begin处的坑
        while (begin < end && array[end] >= key)
            end--;
        if(begin < end)
        {
            array[begin] = array[end];
            begin++;
        }
    }
    
    // 最后只剩下begin和end同时指向的坑，用最初挖掉的基准值填充
    //最终返回begin位置即为替换过来的基准值的位置
    array[begin] = key;
    return begin;    
}

结果同上

快速排序的特性总结：

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(logN)

4. 稳定性：不稳定（隔着位置交换，所以不稳定）

5. 数据量越大越随机越好

最优的情况：每次换分都可以对区间进行均分，基准值左右区间元素个数一样

最差的情况：每次划分时取的基准值都是极值----->O(N²)

当区间接近有序的时候，情况非常差，可以采用三数取中的方式进行优化

假设每次取到的基准值刚好可以将区间划分成左右相等的两部分

程序递归调用图解刚好是一个平衡二叉树

最佳情况下时间复杂度：取决于树的高度，树的高度取决于元素个数

二叉平衡树高度 $\large log_{2}^{N+1}$ （N表示结点个数）每一层消耗的时间都是O（N）

所以快排的最佳时间复杂度为二叉平衡树高度*一层的时间复杂度：O(N*logN)

最差为 O(N²) （每次基准值取的都是极值）时间复杂度要看最差的情况

三数取中法：区间最左侧，最右侧和最中间

// 三数取中法：三个数据取最中间的数据作为基准值
int GetMiddleIndex(int array[], int left, int right)
{
	int mid = left + ((right - left) >> 1);

	// 三个数据：left、mid、right-1
	if (array[left] < array[right - 1])
	{
		if (array[mid] < array[left])
			return left;
		else if (array[mid] > array[right - 1])
			return right - 1;
		else
			return mid;
	}

    // array[left] > array[right - 1]
	else 
	{
		if (array[mid] > array[left])
			return left;
		else if (array[mid] < array[right - 1])
			return right - 1;
		else
			return mid;
	}
}

各取一个数据，以三个数据中的中间值作为基准值,并将选出的基准值放在最右侧

改进后的代码

int Partion1(int array[], int left, int right)
{
    int begin = left;
    int end = right - 1;
    int keyofindex = GetMiddleIndex(array, left, right); // 返回中间值的位置
    if (keyofindex != right - 1)                         // 看基准值是否在最右侧
        Swap(&array[keyofindex] , &array[right-1]);
    int key = array[right - 1];                          // 选最右侧的元素为基准值

    while (begin < end)
    {
        // 让begin从前往后找，找比基准值大的元素，找到就停下来
        while (begin < end && array[begin] <= key)
            begin++;

        // 让end从后往前找，找比基准值小的元素，找到就停下来
        while (begin < end && array[end] >= key)
            end--;

        // 全都找到后交换begin和end位置的元素
        Swap(&array[begin], &array[end]);
    }

    // 当begin和end重合后,先判断begin的位置是否也是right-1处，如果不在，将基准值key交换过去
    if (begin != right - 1)
        Swap(&array[begin], &array[right - 1]);

    return begin;//最终返回begin位置即为基准值的位置
}


int Partion2(int array[], int left, int right)
{
	int begin = left;
	int end = right - 1;
	int keyofindex = GetMiddleIndex(array, left, right);
	int key;
	if (keyofindex != right - 1)
		Swap(&array[keyofindex], &array[right - 1]);

	key = array[right - 1];

	while (begin < end)
	{
		// end位置形成了一个新的坑
		// 让begin从前往后找比基准值大的元素
		while (begin < end && array[begin] <= key)
			begin++;

		// 让begin位置大的元素填end位置的坑
		if (begin < end)
		{
			array[end] = array[begin];
			end--;
		}


		// begin位置形成了一个新的坑
		// 让end从后往前找比基准值小的元素，填begin位置的坑
		// 让end从后往前找，找比基准值小的元素，找到了就停下来
		while (begin < end && array[end] >= key)
			end--;

		if (begin < end)
		{
			array[begin] = array[end];
			begin++;
		}
	}

	// 用基准值填最后的一个坑
	array[begin] = key;
	return begin;
}