3-- 支持向量机贝叶斯_支持向量机中权重计算公式是什么?样本集中哪些样本对权重的计算有意义?-优快云博客

本周学习内容：

学习支持向量机相关内容
学习贝叶斯分类器相关内容

1，支持向量机

1.1 支持向量机基本型

支持向量机是一种分类器，对于做出标记的两组向量，给出一个最优分割超平面把这两组向量分割到两边，使得两组向量中离此超平面最近的向量（即所谓支持向量）到此超平面的距离都尽可能远。

设n维向量空间中有m个向量X1~Xm，每个向量Xi都对应一个标签yi，其中一部分向量的标签值1，另一部分向量的标签值是-1。在n维向量空间中构造一个超平面，在将样本正确分类的同时，使得在超平面两侧找到的支持向量（即距离超平面几何距离最短的向量）到此超平面的距离尽可能远。

超平面方程为：

则该距离为：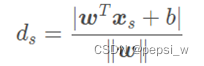

即原始目标可转变为如下求条件最值问题，这就是支持向量机的基本型：

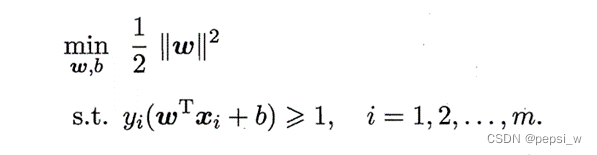
-------（1.1）

1.2 SVM求解

使用拉格朗日乘子法对式1.1进行求解，得到的拉格朗日函数为：

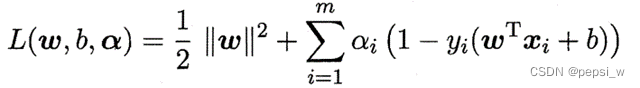
令L(w，b,α)对w和b的偏导为零，并带回原式有：

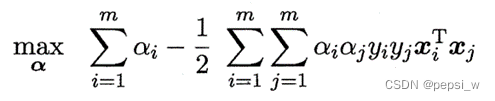
继续对α进行求极大值，带入数据后得到α之间的关系，最终解出w和b

1.3 软间隔

在实际问题中，总有可能偶尔出现异常数据，比如个别正标向量跑到了负标向量堆里去了，如果严格分类会造成一部分向量与决策面很近，甚至根本无法分界。如图1中实线所示，为了容忍个别异常数据，提升模型鲁棒性，实现图1中虚线分类效果：

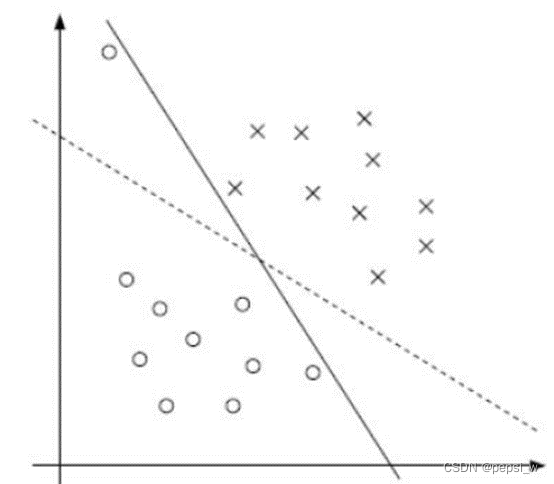
图1

需要对原条件最值问题做调整如下：

其中C>0，为常数，是“0/1损失函数”。当C为无穷大时，迫使所有样本满足约束，当C取有限值表示允许一些样本不满足约束。

1.4 核函数

当原样本空间没有存在一个能正确划分两类样本的超平面，就需要将样本从原始空间映射到一个更高维的特征空间，但维度的提高，会造成极大的计算量。因此需找到一种方法，使得两个低维向量无需向高维空间做映射，只需在原维度空间做简单运算，所得结果就等于其映射到高维空间后的内积，这种方法就是核函数。常用的核函数有以下几种：

线性核。就表示原空间内积，适用于线性可分问题。
高斯核。适用于没有先验经验的非线性分类。其中σ越小，使得映射的维度越高。
多项式核。适用于没有先验经验的分类。其中d越小，使得映射的维度越高。
Sigmoid核。此时SVM实现的就是一种多层感知器神经网络。

1.5 硬间隔分类实现

这里直接使用sklearn库中的鸢尾花数据集，包含 3 类分别为山鸢尾（Iris-setosa）、变色鸢尾（Iris-versicolor）和维吉尼亚鸢尾（Iris-virginica），共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度。

首先对数据集进行选择，这里只使用鸢尾花的两个特征以及两个种类。对数据的处理代码如图2所示：

图2 数据处理代码

    绘制分解超平面与边界的函数plot_svc_decision_boundary()主要代码如图3所示：

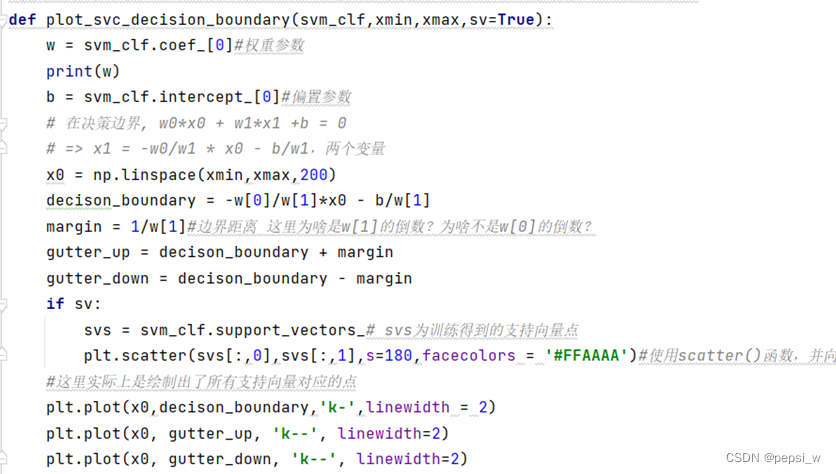
图3 plot_svc_decision_boundary函数

可视化部分仍然使用matplotlib.pyplot模块进行绘图，运行结果如图4所示：

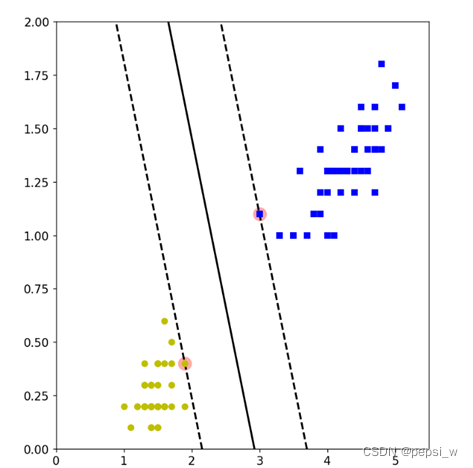
图4 运行结果

1.6 软间隔分类实现

在Scikit-Learn的SVM类中，可以通过超参数C来控制这个平衡，如图5所示，分别是在C值为1和100时在同样数据集上的超平面的划分，可以看出当C值越小，则间隔越宽，但是间隔中的错误例也会越多：

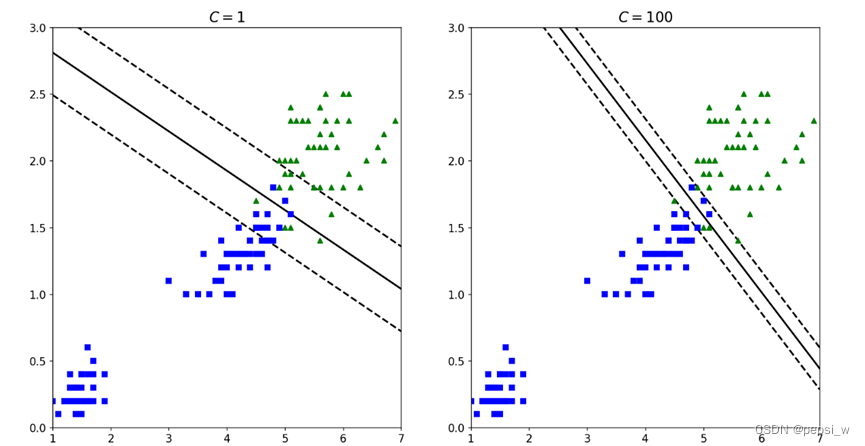
图5 C=1与C=100的决策平面

2，贝叶斯分类器

2.1贝叶斯公式

通过已获得的数据算得先验概率，再通过朴素贝叶斯算法得到各事件的后验概率，认为最大的后验概率所对应的事件的类作为分类的结果。贝叶斯公式如下：

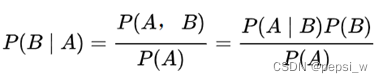
2.2朴素贝叶斯分类器

基于各属性都相互独立的假设下（虽然该假设可能并不符合实际情况，但在该假设下的一些模型的预测准确率足够用以做出决策，因此可以忽略条件独立性假设造成的误差）。后验概率的计算用到贝叶斯定理：

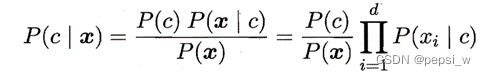
由于我们只需要得到哪种可能性更大，不需要得到各个可能性的准确值，该公式可以化简为：

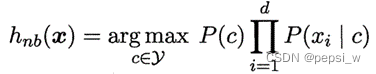
当测试集中某个样本的某个特征的取值，从来没有在训练集中出现过的时候，就需要进行拉普拉斯修正。对于先验概率，拉普拉斯平滑在其分子加1，在分母加上类别的数量 K。对于条件概率，则是在分子加1，在分母加上该特征的可取值的数量。

2.3 半朴素贝叶斯分类器

朴素贝叶斯的基础是各属性都相互独立，但这与实际问题往往不太符合，半朴素允许每个特征依赖且仅依赖除它之外的另外一个特征，基于这个假设提出了独依赖估计（One Dependent Estimator，ODE）分类器。基于不同的依赖特征的选择方法，ODE 又可以分为超父独依赖估计（Super Parent ODE，SPODE），平均独依赖估计（Averaged ODE，AODE）和树增广朴素贝叶斯（Tree Augmented Naive Bayes，TAN）。

1）超父独依赖估计（Super Parent ODE，SPODE）

其特点是所有的特征都依赖于唯一的一个特征，这个被依赖的特征即为 “超父”。公式改写为（其中Xj为超父，通交叉验证来进行选择）：

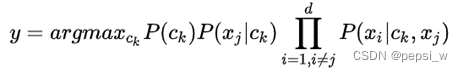
2）平均独依赖估计（Averaged ODE，AODE）

AODE 是基于 SPODE，通过集成学习得到的一个独依赖分类器，与 SPODE 的不同在于，SPODE 是选择一个模型来进行预测，而在 AODE 中，每个模型都进行一次预测，然后将预测结果进行平均后得到最终的预测结果。

3）树增广朴素贝叶斯（Tree Augmented Naive Bayes，TAN）

不管是单个 SPODE 还是多个 SPODE 集成，都是每个模型中每个特征都依赖于超父特征，但是现实情况中，特征的依赖情况也不大可能都依赖于其中之一，而是可能每个特征的依赖都不一样。就可以通过TAN 可以找到每个特征最适合依赖的另外一个特征。TAN 计算两两特征之间的条件互信息，在选择每个特征的依赖特征时，选择互信息最大的对应特征即可。

计算条件互信息公式为：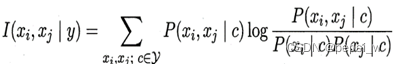

附：

#SVM基于鸢尾花数据集的实现 核函数使用线性核函数
from sklearn.svm import SVC
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['axes.labelsize'] = 14#设置子图的标签大小
plt.rcParams['xtick.labelsize'] = 12#设置横轴字体大小
plt.rcParams['ytick.labelsize'] = 12#设置纵轴字体大小
#import warnings
#warnings.filterwarnings('ignore')#调用  warnings  模块中定义的  warn()  函数来发出警告。

iris = datasets.load_iris()#花萼长度sepal length , 花萼宽度sepal width, 花瓣长度petal length , 花瓣宽度petal width 三个种类 0，1，2
X = iris['data'][:,(2,3)]#选取iris中data数据第2、3属性 即花瓣长度petal length , 花瓣宽度petal width
y = iris['target']#获取种类

setosa_or_versicolor = (y==0)|(y==2)#这里只选两类数据
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]


svm_clf = SVC(kernel="linear",C=float('inf'))#核函数选择线性，惩罚参数为正无穷，即选择让所有样本点都满足条件
svm_clf.fit(X,y)


x0 = np.linspace(0,5.5,200)#在0到5.5的范围内返回200个等间隔的数
pred_1 = 5*x0 -20
pred_2 = x0-1.8
pred_3 = 0.1*x0 + 0.5

#函数作用：绘制分界超平面和边界距离
#使支持向量机的权重等于w，偏置等于b，黑色的实线表示决策边界，黑色虚线表示最近点的样本的位置
def plot_svc_decision_boundary(svm_clf,xmin,xmax,sv=True):
    w = svm_clf.coef_[0]#权重参数
    print(w)
    b = svm_clf.intercept_[0]#偏置参数
    # 在决策边界, w0*x0 + w1*x1 +b = 0 这里可以理解为我已经知道这个决策平面的方程 但是要画出来 其中先随机选取一个变脸x，再根据方程来解出另一个值（这里就是decison_boundary 也就是y值）这样才能画出来
    # => x1 = -w0/w1 * x0 - b/w1，两个变量
    x0 = np.linspace(xmin,xmax,200)#在xmin-xmax之间生成200个等间距数组
    decison_boundary = -w[0]/w[1]*x0 - b/w[1]
    margin = 1/w[1]#边界距离 这里为啥是w[1]的倒数？为啥不是w[0]的倒数？
    gutter_up = decison_boundary + margin
    gutter_down = decison_boundary - margin
    if sv:
        svs = svm_clf.support_vectors_# svs为训练得到的支持向量点
        plt.scatter(svs[:,0],svs[:,1],s=180,facecolors = '#FFAAAA')#使用scatter()函数，并向它传递一对x和y坐标，它将在指定位置绘制一个点
    #这里实际上是绘制出了所有支持向量对应的点
    plt.plot(x0,decison_boundary,'k-',linewidth = 2)
    plt.plot(x0, gutter_up, 'k--', linewidth=2)
    plt.plot(x0, gutter_down, 'k--', linewidth=2)
#可视化部分
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,6))#设定nn排列方式，这里设置的是22，nrows行，ncols列，figsize设定窗口大小，使用的时候可以按照需求设定图片排版格式

plt.sca(axes[0])#第一个图片
plt.plot(x0, pred_1, "g--", linewidth=2)#pred_1用绿色的虚线
plt.plot(x0, pred_2, "m-", linewidth=2)#pred_2粉紫色的实线
plt.plot(x0, pred_3, "r-", linewidth=2)#pred_3红色的实线
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")#“bs”蓝色的方块  X[:, 0][y==1]表示y=1种类的横坐标, X[:, 1][y==1]表示y=1种类的纵坐标 这里横纵坐标是那两个属性
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.axis([0, 5.5, 0, 2])#坐标轴范围

plt.sca(axes[1])#第二个图片
plot_svc_decision_boundary(svm_clf, 0, 5.5)#调用函数
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")#“bs”蓝色的方块
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "yo")#“yo”黄色的圆圈
plt.axis([0, 7.5, 0, 3.5])
plt.show()

#对比硬软间隔的效果
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt

plt.rcParams['axes.labelsize'] = 14#设置子图的标签大小
plt.rcParams['xtick.labelsize'] = 12#设置横轴字体大小
plt.rcParams['ytick.labelsize'] = 12#设置纵轴字体大小

iris = datasets.load_iris()
X = iris['data'][:,(2,3)]
y = (iris["target"] == 2).astype(np.float64)
svm_clf = Pipeline((
    ('std',StandardScaler()),
    ('linear_svc',LinearSVC(C=1)) ))
svm_clf.fit(X,y)

scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1,loss="hinge",random_state=42)
svm_clf2 = LinearSVC(C=100,loss="hinge",random_state=42)

scaled_svm_clf1 = Pipeline((
    ('std',scaler),
    ('linear_svc',svm_clf1) ))
scaled_svm_clf1.fit(X,y)

scaled_svm_clf2 = Pipeline((
    ('std',scaler),
    ('linear_svc',svm_clf2) ))
scaled_svm_clf2.fit(X,y)
# 转换为未缩放的参数 这段代码很重要 不然那个线画不出来
#decision_function()的功能：计算样本点到分割超平面的函数距离
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])# standardScaler.mean_：查看均值
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_#standardScaler.scale_：查看标准差
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
#函数作用：绘制分界超平面和边界距离
#使支持向量机的权重等于w，偏置等于b，黑色的实线表示决策边界，黑色虚线表示最近点的样本的位置
def plot_svc_decision_boundary(svm_clf,xmin,xmax):
    w = svm_clf.coef_[0]#权重参数
    print(w)
    b = svm_clf.intercept_[0]#偏置参数
    # 在决策边界, w0*x0 + w1*x1 +b = 0
    # => x1 = -w0/w1 * x0 - b/w1，两个变量
    x0 = np.linspace(xmin,xmax,200)
    decison_boundary = -w[0]/w[1]*x0 - b/w[1]
    margin = 1/w[1]#边界距离 这里为啥是w[1]的倒数？为啥不是w[0]的倒数？
    gutter_up = decison_boundary + margin
    gutter_down = decison_boundary - margin
    #这里实际上是绘制出了所有支持向量对应的点
    plt.plot(x0,decison_boundary,'k-',linewidth = 2)
    plt.plot(x0, gutter_up, 'k--', linewidth=2)
    plt.plot(x0, gutter_down, 'k--', linewidth=2)

fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,6))#设定nn排列方式，这里设置的是22，nrows行，ncols列，figsize设定窗口大小，使用的时候可以按照需求设定图片排版格式

plt.sca(axes[0])#第一个图片
plot_svc_decision_boundary(svm_clf1, 1, 7)#调用函数
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")#“bs”蓝色的方块  X[:, 0][y==1]表示y=1种类的横坐标, X[:, 1][y==1]表示y=1种类的纵坐标 这里横纵坐标是那两个属性
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.axis([1, 7, 0, 3])#坐标轴范围
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)

plt.sca(axes[1])#第二个图片
plot_svc_decision_boundary(svm_clf2, 1, 7)#调用函数
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")#“bs”蓝色的方块
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")#“yo”黄色的圆圈
plt.axis([1, 7, 0, 3])#坐标轴范围
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.show()

下周计划：